(paper) Transformers in Time Series ; A Survey

Transformers in Time Series : A Survey (2022)

Contents

1. Introduction

2. Preliminaries of the Transformer
   1. Vanilla Transformer
   2. Input Encoding & Positional Encoding
   3. Multi-head Attention
   4. FFNN & Residual Network
3. Network Modifications for TS
   1. Positional Encoding
   2. Attention Module
4. Applications of TS Transformers
   1. TS in Forecasting
   2. TS in Anomaly Detection

1. Introduction

Transformers :

• great modeling ability for LONG range dependencies / interatcions in SEQUENTIAL data

Summarize the development of time series Transformers

2. Preliminaries of the Transformer

(1) Vanilla Transformer

• skip

(2) Input Encoding & Positional Encoding

Transformer : no recurrence / no convolution

ABSOLUTE positional encoding

\(P E(t)_{i}= \begin{cases}\sin \left(\omega_{i} t\right) & i \% 2=1 \\ \cos \left(\omega_{i} t\right) & i \% 2=0\end{cases}\).

• \(\omega_{i}\) : hand-crafted frequency for each dimension

( or, can “LEARN” PE )

RELATIVE positional encoding

• pairwise positional relationships between input elements

HYBRID positional encoding

(3) Multi-head Attention

\(\operatorname{Attention}(\mathbf{Q}, \mathbf{K}, \mathbf{V})=\operatorname{softmax}\left(\frac{\mathbf{Q K}^{\mathbf{T}}}{\sqrt{D_{k}}}\right) \mathbf{V}\).

• \(\mathbf{Q} \in \mathcal{R}^{N \times D_{k}}\).
• \(\mathbf{K} \in \mathcal{R}^{M \times D_{k}}\).
• \(\mathbf{V} \in \mathcal{R}^{M \times D_{v}}\).
• \(N, M\) denote the lengths of queries and keys (or values)

uses multi-head attention with \(H\) different sets

• \(\operatorname{MultiHeadAttn}(\mathbf{Q}, \mathbf{K}, \mathbf{V})=\) Concat \(\left(\right.\) head \(_{1}, \cdots\), head \(\left._{H}\right) \mathbf{W}^{O}\)

  • \(h e a d_{i}=\) Attention \(\left(\mathbf{Q} \mathbf{W}_{i}^{Q}, \mathbf{K} \mathbf{W}_{i}^{K}, \mathbf{V} \mathbf{W}_{i}^{V}\right)\)

• \(\operatorname{MultiHeadAttn}(\mathbf{Q}, \mathbf{K}, \mathbf{V})=\) Concat \(\left(\right.\) head \(_{1}, \cdots\), head \(\left._{H}\right) \mathbf{W}^{O}\) where \(h e a d_{i}=\) Attention \(\left(\mathbf{Q} \mathbf{W}_{i}^{Q}, \mathbf{K} \mathbf{W}_{i}^{K}, \mathbf{V} \mathbf{W}_{i}^{V}\right)\) 2.4 Feed-forward and Residual Network The point-wise feed-forward network is a fully connected module as

\(F F N\left(\mathbf{H}^{\prime}\right)=\operatorname{Re} L U\left(\mathbf{H}^{\prime} \mathbf{W}^{1}+\mathbf{b}^{1}\right) \mathbf{W}^{2}+\mathbf{b}^{2},\) where \(\mathbf{H}^{\prime}\) is outputs of previous layer, \(\mathbf{W}^{1} \in \mathcal{R}^{D_{m} \times D_{f}}\), \(\mathbf{W}^{2} \in \mathcal{R}^{D_{f} \times D_{m}}, \mathbf{b}^{1} \in \mathcal{R}^{D_{f}}, \mathbf{b}^{2} \in \mathcal{R}^{D_{m}}\) are trainable parameters. In a deeper module, a residual connection module followed by Layer Normalization Module is inserted around each module. That is, \(\begin{aligned} \mathbf{H}^{\prime} &=\operatorname{Layer} N \operatorname{orm}(\operatorname{Self} \operatorname{Attn}(\mathbf{X})+\mathbf{X}), \\ \mathbf{H} &=\text { Layer } N \operatorname{orm}\left(F F N\left(\mathbf{H}^{\prime}\right)+\mathbf{H}^{\prime}\right) \end{aligned}\) where SelfAttn(.) denotes self attention module and LayerNorm(.) denotes the layer normal operation.

(4) FFNN & Residual Network

\(F F N\left(\mathbf{H}^{\prime}\right)=\operatorname{Re} L U\left(\mathbf{H}^{\prime} \mathbf{W}^{1}+\mathbf{b}^{1}\right) \mathbf{W}^{2}+\mathbf{b}^{2}\)/

• \(\mathbf{H}^{\prime}\) : output of previous layer

Residual Network

• residual connection module followed by Layer Normalization Module
• \(\mathbf{H}^{\prime}=\operatorname{Layer} N \operatorname{orm}(\operatorname{Self} \operatorname{Attn}(\mathbf{X})+\mathbf{X})\).
• \(\mathbf{H} =\text { Layer } N \operatorname{orm}\left(F F N\left(\mathbf{H}^{\prime}\right)+\mathbf{H}^{\prime}\right)\).

3 .Network Modifications for TS

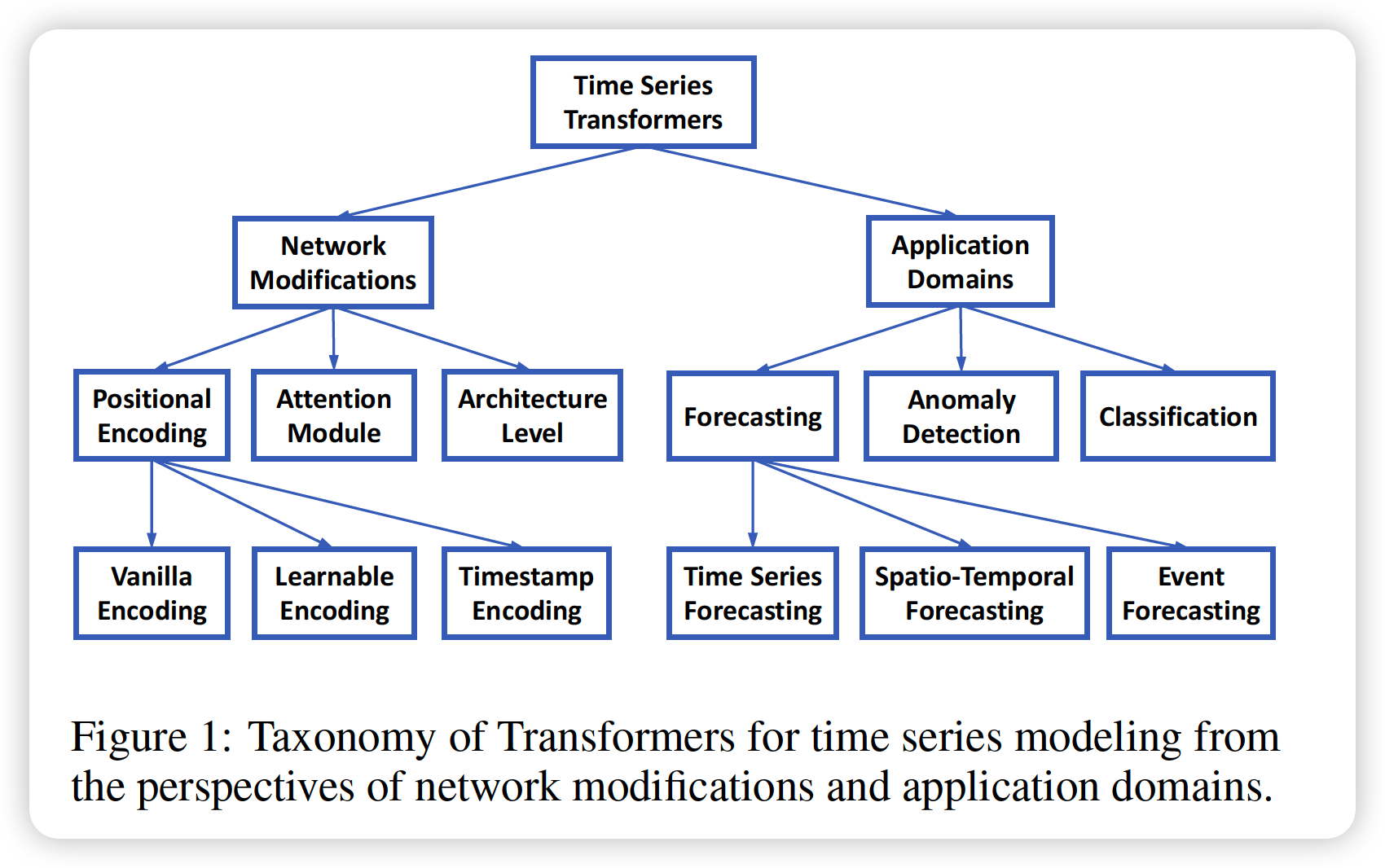
(1) Positional Encoding

( not much different

a) Vanilla PE

b) Learnable PE

• more flexible & adapt itself to specific task

c) Timestamp Encoding

• calendar timestamps
• Informer (2021)
  • encode timestamps as additional positional encoding

(2) Attention Module

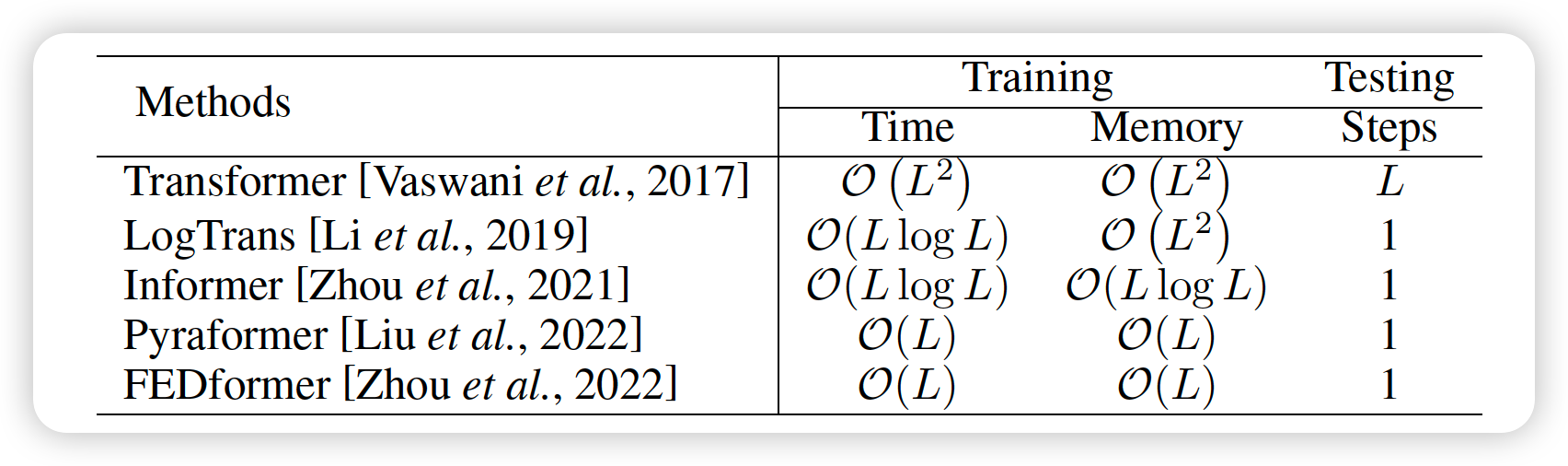
Self attention : \(O(L^2)\)

• \(L\) : input TS length

• computational bottleneck ( when long TS )

Reducing quadratic complexity!

• ex) LogTrans, Performer,…

(3) Architecture level Innovation

Informer

• insert max-pooling layers with stride=2

Pyraformer

• C-ary tree based attention mechanism

Both INTRA & INTER scale attentions capture temporal dependencies across different resolutions

4. Applications of TS Transformers

[ TS in Forecasting ]

Time Series Forecasting

LogTrans

• convolution self-attention ( use causal convolutions )
• Introduce sparse bias
• \(O(L^2) \rightarrow O(L \log L)\).

Informorer

• instead of introducing sparse bias,
• selects \(O(\log L)\) dominant queries, based on (queries & key) similarities

AST

• GAN framework
• train sparse transformer for TS forecasting

Autoformer

• simple ST decomposition
• auto-correlation mechansim working as an attention module

FEDformer

• applies attention operation in the frequency domain

  ( with Fourier transform & Wavelet transform )

TFT

• multi-horizon forecasting model, with
  • static covariate encoder
  • gating feature selection
  • temporal self-attention decoder

SSDNet & ProTran

• combine “Transformer” + “SSM (State Space Model)”
• SSDNet
  • use Transformer to learn the temporal pattern
  • estimate the parameters of SSM
  • then applies SSM to perform the ST decomposition & interpretability
• ProTran
  • generative modeling & inference, using VI

Pyraformer

• hierarchical pyramidal attention module
• with binary tree following path

Aliformer

• sequential forecasting for TS
• use Knowledge-guided attention

###

Traffic Transformer

• use self-attention…
  • to capture temporal-temporal dependencies
• use GNN…
  • to capture spatial dependencies

Spatial-temporal Transformer

• spatial transformer block + GCN,

  to better capture spatial-spatial dependencies

Spatio-temporal graph Transformer

• attention-based GCN
• able to learn a complicated temporal-spatial attentions

[ TS in Anomaly Detection ]

Reconstruction model plays a key role in AD tasks

Transformer based AD : much more efficient than LSTM based

TranAD

• proposes an adversarial training procedure, to amplify reconstruction errors
• GAN style adversarial training procedure :
  • 2 Transformer encoders
  • 2 Transformer decoders

TransAnomaly

• VAE + Transformer

• ror more parallelization

  ( reduce training cost by 80% )

MT-RVAE

• multiscale Transformer
• integrate TS information at different scales

GTA

• combine Transformer & Graph based learning architecture