( 참고 : Fast Campus 금융공학/퀀트 강의 )
2. 시계열 데이터 분해법
(1) 이동 평균
단순 이동 평균 (Moving Average)
- 과거의 모든 시점을 동일(Uniform)하게 가중치 부여
gs_price = ts(gs$$price, frequency = 250)
m1 = filter(gs_price, rep(1/100,100), sides=1)
지수 이동 평균 (Exponential Moving Average)
- 과거의 모든 시점을 다르게(Non-Uniform)하게 가중치 부여
- 최근일수록 가중치 \(\uparrow\)
\(S_{t}= \begin{cases}Y_{1}, & t=1 \\ \alpha \cdot Y_{t}+(1-\alpha) \cdot S_{t-1}, & t>1\end{cases}\),
\(\begin{aligned} S_{t}=\alpha &\left[Y_{t-1}+(1-\alpha) Y_{t-2}+(1-\alpha)^{2} Y_{t-3}+\cdots\right.\\ &\left.\cdots+(1-\alpha)^{k} Y_{t-(k+1)}\right]+(1-\alpha)^{k+1} S_{t-(k+1)} \end{aligned}\).
- \(\alpha\) 가 크면 클수록 최근성에 더 높은 가중치
HoltWinters 함수를 사용하여 계산 가능
-
argument
alpha를 지정해주지 않으면, 자동으로 최적 alpha 계산 -
(참고) HoltWinters는 시계열을
- 1) level(L)
- 2) trend(b)
- 3) seasonality(s)
셋으로 분해한다
gs_hw = HoltWinters(gs_price, alpha = 0.8, beta=FALSE, gamma=FALSE)
(2) 시계열의 분해
계절성 : Frequency
일정하게 반복되는 시계열의 계절성을 계산하기 위해,
ts함수에서 argument frequency를 정해줘야!
-
ex) 초단위로 기록되는 데이터 & 1시간마다의 계절성
\(\rightarrow\)
frequencey= 1시간 = 3600초
Holt Winters
\[\begin{aligned} \hat{y}_{t+h \mid t} &=\ell_{t}+h b_{t}+s_{t-m+h_{m}^{+}} \\ \ell_{t} &=\alpha\left(y_{t}-s_{t-m}\right)+(1-\alpha)\left(\ell_{t-1}+b_{t-1}\right) \\ b_{t} &=\beta^{*}\left(\ell_{t}-\ell_{t-1}\right)+\left(1-\beta^{*}\right) b_{t-1} \\ s_{t} &=\gamma\left(y_{t}-\ell_{t-1}-b_{t-1}\right)+(1-\gamma) s_{t-m}, \end{aligned}\]
분해 요소 해석
-
1) \(l(t)\) = level
- 현재 & (가중평균된) 과거와의 (가중) 평균
- weight = \(\alpha\) ( 지수 이동 평균 )
-
2) \(b(t)\) = trend
-
현재 기울기 & 과거 기울기와의 가중 평균
( 기울기 : 직전 데이터 대비 증감 )
-
weight = \(\beta\)
-
-
3) \(s(t)\) = seasonality
- (데이터에서 level & trend를 제거한) 직전 seasonal & 현재 seasonal의 가중 평균
R 코드
HoltWinters(x, alpha = NULL, beta = NULL, gamma = NULL,
seasonal = c("additive", "multiplicative"),
start.periods = 2,
l.start = NULL, b.start = NULL, s.start = NULL,
optim.start = c(alpha = 0.3, beta = 0.1, gamma = 0.1),
optim.control = list())
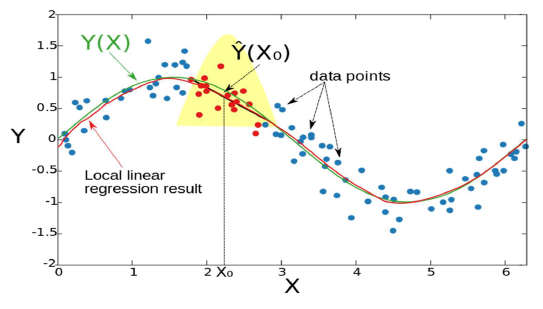
STL (Seasonal Decomposition of Time Series by LOESS)
LOESS
-
LOcal reGreSSION
( = locally weighted polynomial regression )3
R 코드
gs_price = ts(gs$$price, frequency = 250)
# stl 모형 파라미터 계산 (train)
gs_stl= stl(gs_price, s.window = “periodic”)
# Decomposition 그래프
plot(gs_stl)
# 예측
forecast(gs_stl, h=100)
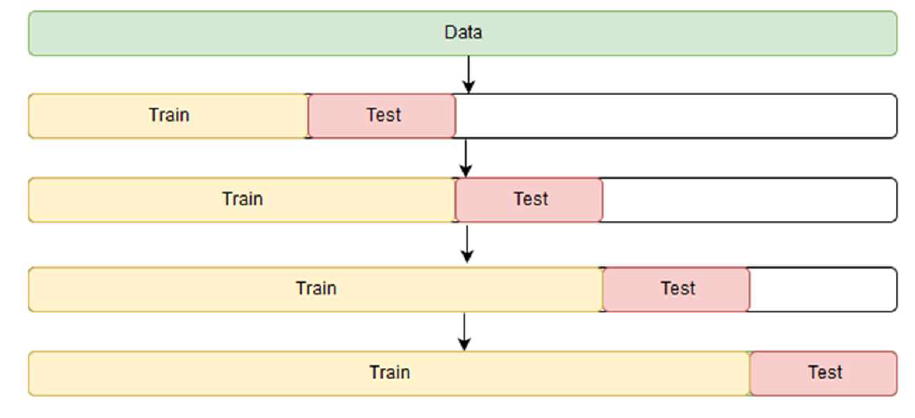
(3) 시계열 Cross-Validation
(4) 시계열 예측
a) 가중 이동 평균
# Modeling set & Test set
AP_ms = AP[1:132]
AP_ts = AP[133:144]
y = ts(AP_ms, frequency=12)
# Exponential Moving Average
fit = HoltWinters(y, beta=FALSE, gamma=FALSE)
fc = forecast(fit, h=12) # 12개월 예측수행
plot(fc, main = "Exponential Moving Average Forecasts")
# 정확도(1-MAPE)
mean(100-100*abs(as.numeric(fc$$mean)-as.numeric(AP_ts))/as.numeric(AP_ts))
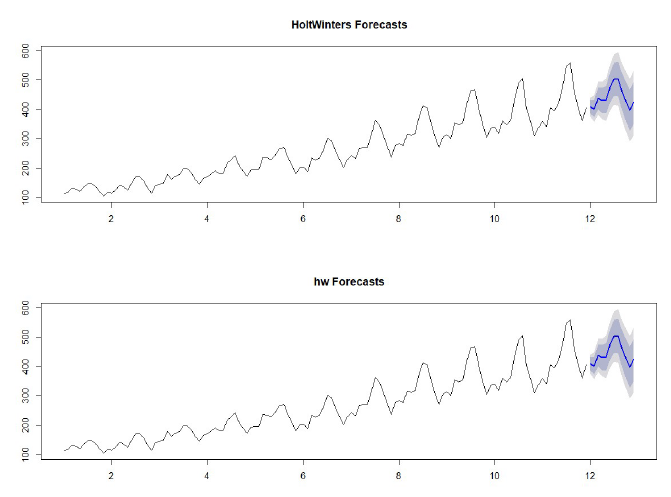
b) HoltWinters 예측
방법 1)
fit = HoltWinters(y)
fc = forecast(fit, h=12)
plot(fc, main = "Exponential Moving Average Forecasts")
방법 2)
fit = hw(y)
fc = forecast(fit, h=12)
plot(fc, main = "Holt-Winters Forecasts")
c) STL 예측
fit = stl(y, s.window = "periodic")
fc3 = forecast(fit, h=20)
plot(fc3, main = "stl Forecasts")
mean(100-100*abs(as.numeric(fc3$$mean)-as.numeric(gs_ts))/as.numeric(gs_ts))
