(TS summary) 3.ARIMA

( 참고 : Fast Campus 금융공학/퀀트 강의 )

3. ARIMA

(1) 시계열의 정상성

상관관계 & 자기상관관계

• 상관관계 : x & y 사이
  • \(r_{x y}=\frac{\sum_{i=1}^{n}\left(x_{i}-\bar{x}\right)\left(y_{i}-\bar{y}\right)}{\sqrt{\sum_{i=1}^{n}\left(x_{i}-\bar{x}\right)^{2} \sum_{i=1}^{n}\left(y_{i}-\bar{y}\right)^{2}}}\).
• 자기상관관계 : 현재 y & 과거 y 사이
  • \(r_{k}=\frac{\sum_{t=k+1}^{n}\left(y_{t}-\bar{y}\right)\left(y_{t-k}-\bar{y}\right)}{\sum_{t=1}^{n}\left(y_{t}-\bar{y}\right)^{2}}\).

정상성 ( Stationary )

시계열의 결합확률분포가 “시간에 따라 변하지 않는다”

\(F_{X}\left(x_{t_{1}+\tau}, \ldots, x_{t_{k}+\tau}\right)=F_{X}\left(x_{t_{1}}, \ldots, x_{t_{k}}\right)\).

약한 정상성 ( Weak Stationary )

3가지 조건

• **1) 평균 일정 **

  \(\rightarrow\) 트렌드가 없음

• 2) 분산 일정

  \(\rightarrow\) 시계열 변화의 폭이 일정

• 3) 자기상관함수(ACF)는 “시간이 아닌 시차(lag)”의 함수

  \(\rightarrow\) 시계열 내의 두 데이터 간의 상관관계는 오직 “시차”에 의해 결정

정상 시계열 vs 비정상 시계열

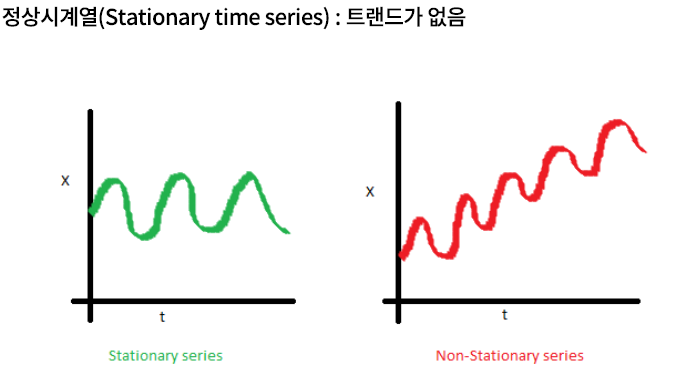
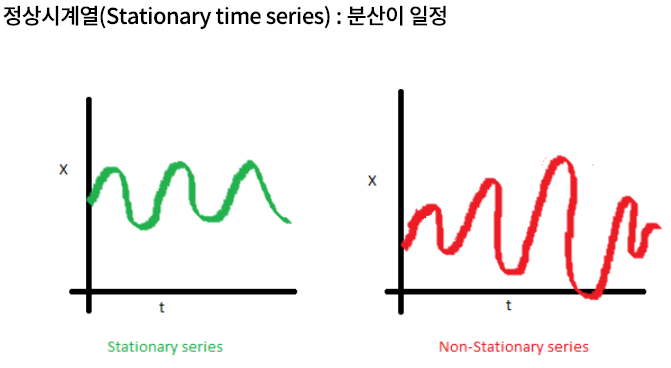
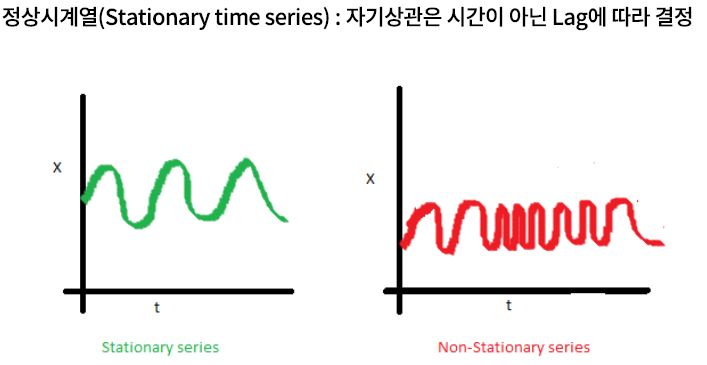
정상 시계열 : White Noise

가장 대표적인 “정상” 시계열 = White Noise (WN)

3가지 특징 (조건)

• \(E\left(u_{t}\right)=0 \quad \forall t\).
• \(\operatorname{Var}\left(u_{t}\right)=\sigma_{u}^{2}<\infty \quad \forall t\).
• \(\operatorname{Cov}\left(u_{t}, u_{t-k}\right)=0 \quad \forall t, \forall k\).

R 코드

white_noise = rnorm(1000)
ts.plot(white_noise)

비정상 시계열 : Random Walk

\(y_{t}=y_{t-1}+\epsilon_{t}\).

• 1) 평균 : 시간에 따라 변하지 않음
• 2) 분산 : 시간에 따라 증가 \(\rightarrow\) non-stationary

x = rnorm(1)
w = rnorm(1000)
for(t in 2:1000){ x[t] = x[t-1] + w[t] }
ts.plot(x)

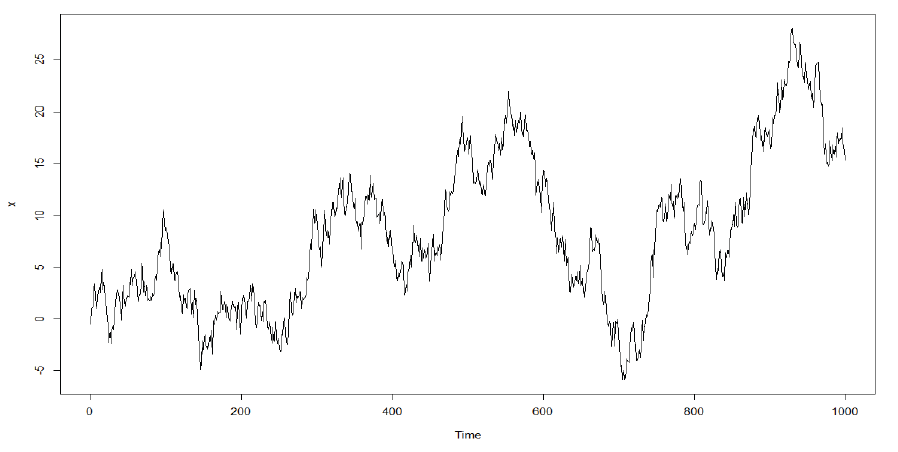
비정상 \(\rightarrow\) 정상

Trend 없애기 : 차분(differencing)

diff(data)

분산 안정시키기 : log

• de-trend 한 이후…

log(diff(AirPassengers))

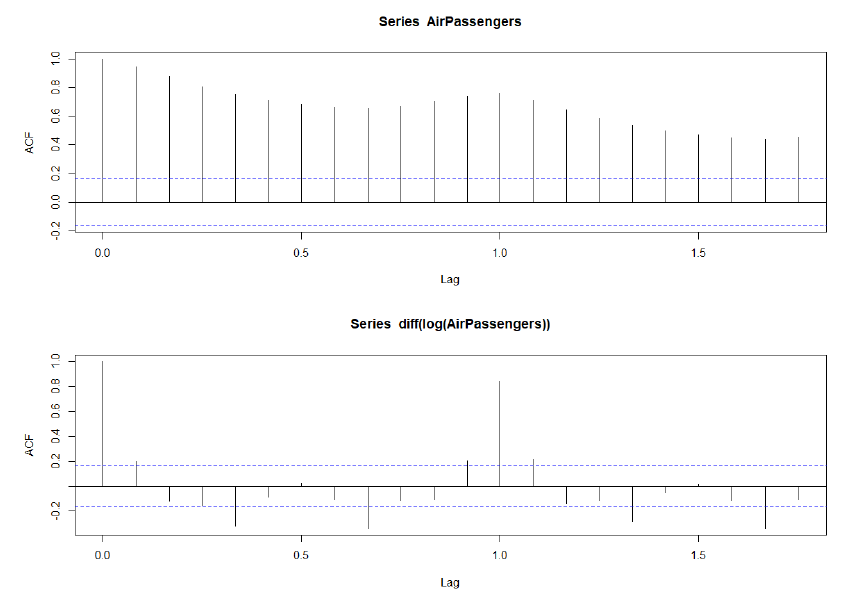
ACF Plot ( 자기상관함수 plot )

• (1) 차분 & (2) 로그 변환 이후, 정상성 시계열로 변화했는지 확인!

par(mfrow=c(2,1))
acf(AirPassengers)
acf(diff(log(AirPassengers)))

(2) ARIMA 모형

\(X_{t}=\sum_{j=1}^{p} \phi_{j} X_{t-j}+\sum_{j=1}^{q} \theta_{j} \omega_{t-j}+\omega_{t}\).

• AR(p) = 자기 상관 모형
  • \(p\) 개의 과거 데이터
• MA(q) = 이동 평균 모형
  • \(q\) 개의 WN
• ARMA = AR(p) + MA(q)
• ARIMA = AR(p) + MA(q) + differencing(차분)

정상성을 만족하는 시계열을 대상으로 ARMA를 fitting해야한다!

AR(p) : 자기 상관 모형(Autoregressive)

\(\begin{aligned} \operatorname{AR}(\mathrm{p}): & X_{t}=\phi_{1} X_{t-1}+\phi_{2} X_{t-2}+\ldots+\phi_{p} X_{t-p}+Z_{t} \\ &\left\{Z_{t}\right\} \sim W N\left(0, \sigma^{2}\right) \end{aligned}\).

ex) AR(1)

\(X_{t}=\alpha X_{t-1}+\omega_{t}\) with \(-1<\alpha<1\)

# sampling ( alpha = 0.9 )
ar1 = arima.sim(n=10000, list(ar=c(0.9)) )
ts.plot(ar1)

\(\phi\) 값의 의미 : \(\phi\)의 절대값이….

• 1보다 작음 : 정상
• 1과 같음 : 비정상 ( Random Walk )
• 1보다 큼 : 비정상 ( Explosive )

\(\begin{aligned} X_{t} &=\phi X_{t-1}+Z_{t} \\ &=\phi\left(\phi X_{t-2}+Z_{t-1}\right)+Z_{t} \\ &=\phi^{2} X_{t-2}+\phi Z_{t-1}+Z_{t} \\ & \vdots \\ &=\phi^{k} X_{t-k}+\sum_{j=0}^{k-1} \phi^{j} Z_{t-j} \end{aligned}\).

(3) Unit Root Test

by ADF (Augmented Dichey-Fuller) Test

위의 \(\phi\)의 근을 구해서, 이것이 1인지 아닌지 구하는 함수

• H0 : 비정상
• H1 : 정상

( 주의 : default로 “차분”을 해준다 )

R 코드 :

adf.test(data)

(4) ARIMA 모델링

\(X_{t}=\sum_{j=1}^{p} \phi_{j} X_{t-j}+\sum_{j=1}^{q} \theta_{j} \omega_{t-j}+\omega_{t}\).

key point : 3개의 파라미터 (p,q,d)를 추정하는 것

• ARIMA = AR(p) + MA(q) + differencing(d)
  • d번의 차분
  • p개의 과거 데이터
  • q개의 WN

step 1) \(d\) 번 차분 후, 정상으로 변환

step 2) ARMA적합하기 위해, acf/pacf를 사용하여 p,q를 찾음

• AR(p)를 구하기 위해선 pacf
• MA(q)를 구하기 위해서는 acf

( 주의 : ARMA는 반드시 “정상 시계열”로 변환 후 fitting 시켜야 )

ACF vs PACF

• ACF : t시점 & t-k시점의 상관관계를 파악
• PACF : t시점 & t-k시점의, (두 시점사이의 영향을 배제한 채) 상관관계를 파악

Example

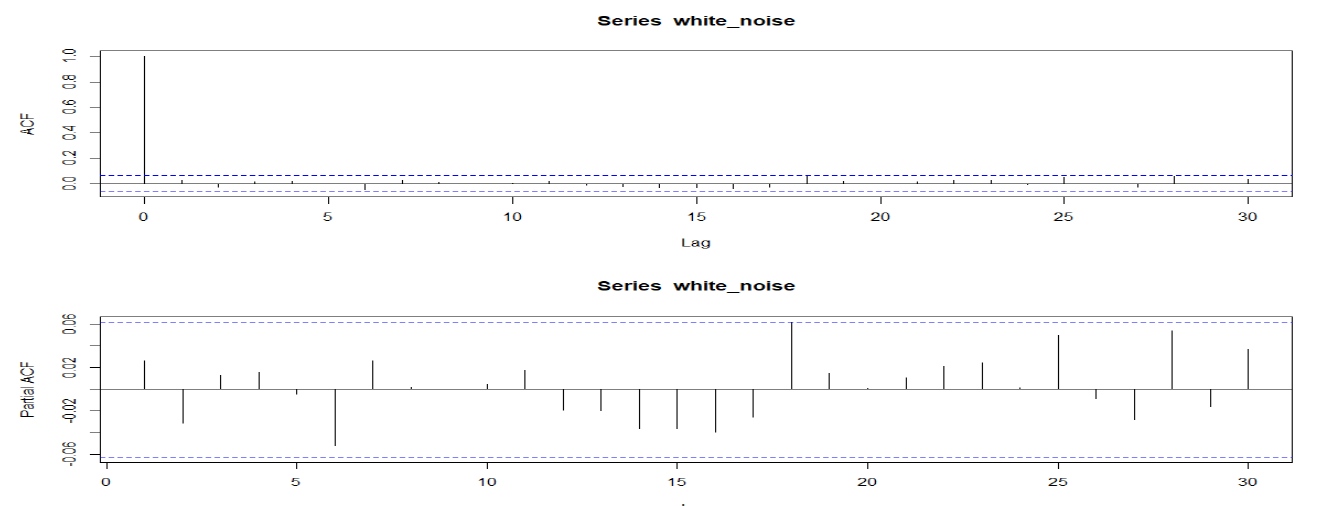
(1) White Noise의 ACF & PACF

• ACF :
  • lag=0 : 1
  • lag=1이상 : 0
• PACF :
  • 항상 : 0

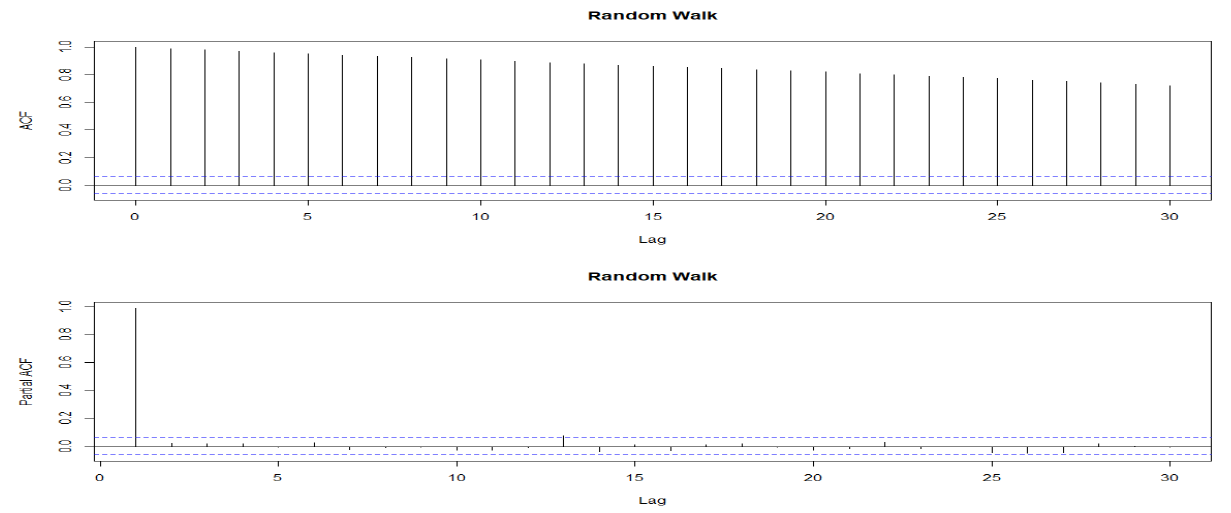
(2) Random Walk의 ACF & PACF

• ACF :
  • 항상 : 큼
• PACF :
  • lag=1 : 큼
  • lag 2 이상 : 0

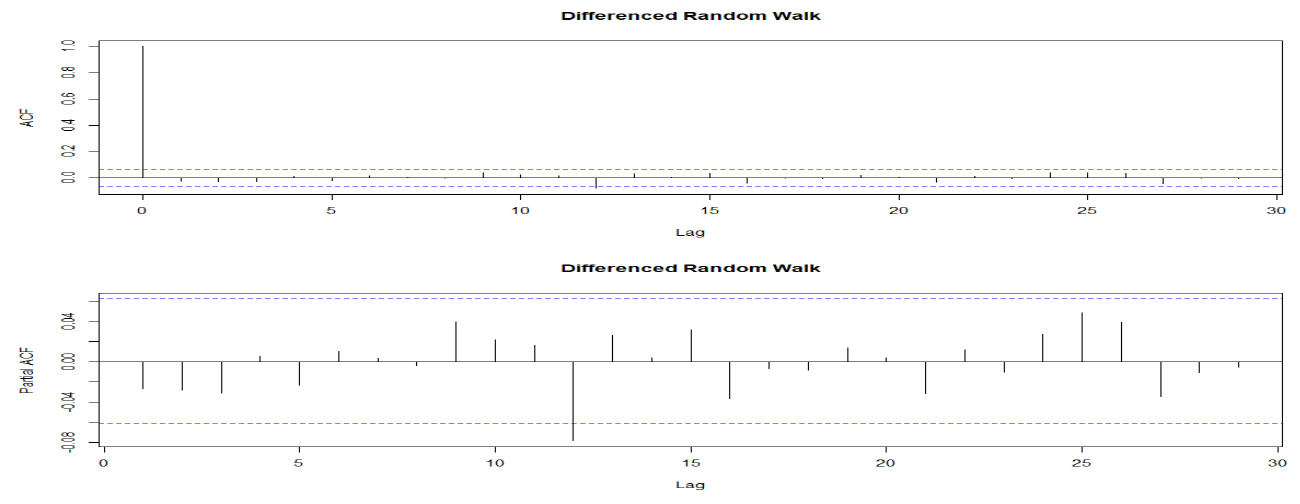
(3) 차분된 Random Walk의 ACF & PACF

• ACF :
  • lag=0 : 1
  • lag=1 이상 : 0
• PACF :
  • 항상 : 0

(5) ARIMA example

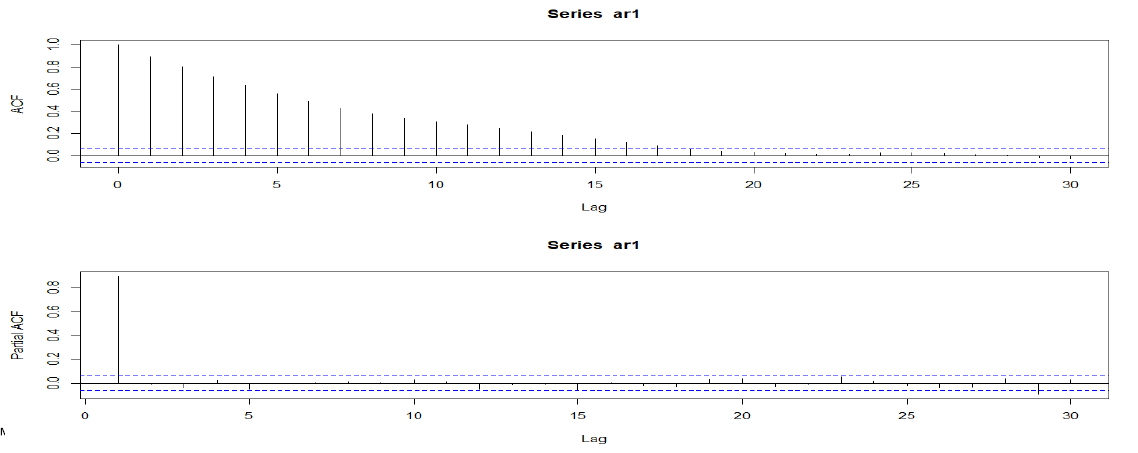
AR(1) : p=1 (\(\alpha=0.9\)), q=0

• ( ACF는 점진적으로 감소 )
• PACF : p=1 시점 이후에 급격히 감소

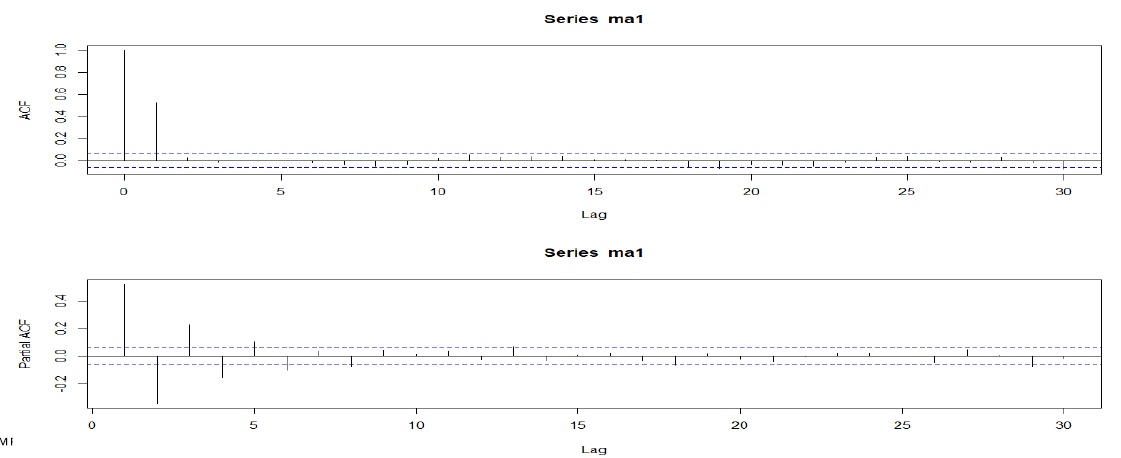
MA(1) : p=0, q=1 (\(\theta=0.8\))

• ACF : q=1 시점 이후에 급격히 감소
• ( PACF는 점진적으로 감소 )

(6) R의 auto.arima

패키지 : forecast

함수 : auto.arima

• 최적의 파라미터 (p,d,q)를 잦동으로 찾아줌

R 코드

auto.arima(AirPassengers)

결과 :

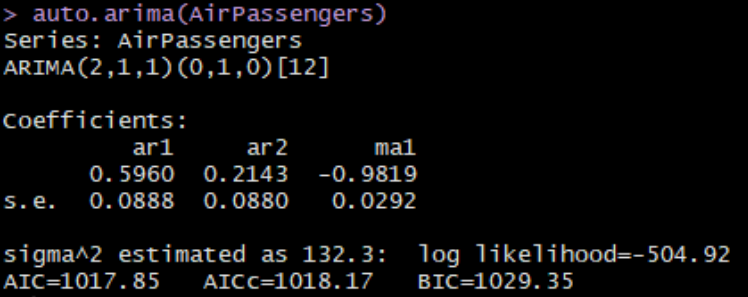
해석

• ARIMA(2,1,1)(0,1,0)[12]
  • (2,1,1) : p=2, d=1, q=1
  • (0,1,0)[12] : 매 12달 마다의 seasonality
• 식 : \(y_t = 0.596*y_{t-1} + 0.2143*y_{t-2} - 0.9819*e_{t-1}\).

ARIMA 파라미터 직접 설정 후 fitting도 가능

arima(AirPasssengers,
      c(2,1,1),
      seasonal = list(order = c(0, 1, 0), period = 12))

Forecast

fit = auto.arima(AirPassengers)
fcst = forecast(fit, h = 10*12) # 10년 (10x12개월) 예측

plot(fcst) # 평균 + 신뢰구간 
plot(fcst$$mean) # 평균