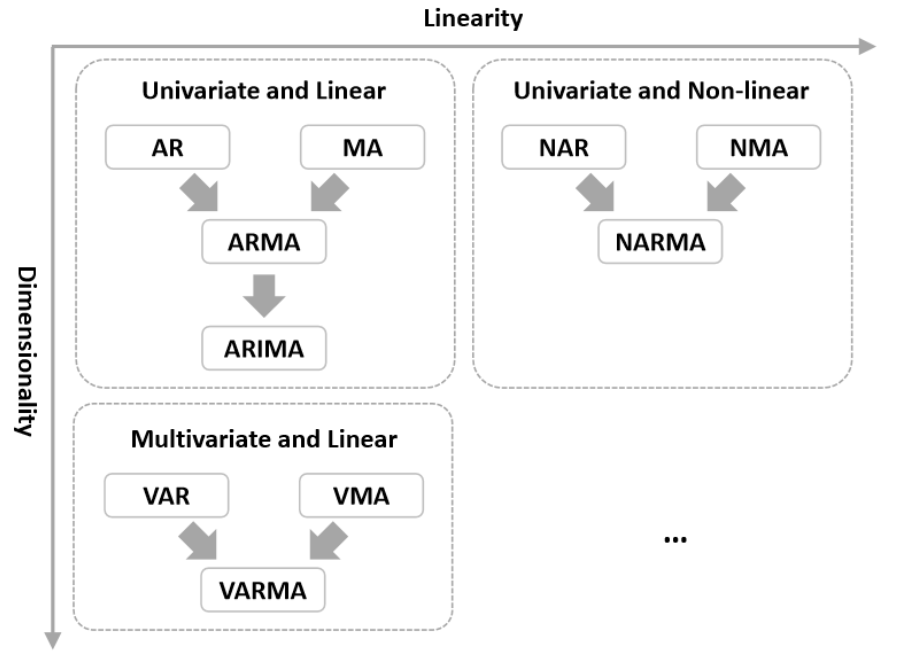
Univariate 1. 정상성 데이터로의 변환
1. Overview
2. 비정상성 \(\rightarrow\) 정상성 methods
-
변환 목적 : 안정성 & 예측력 \(\uparrow\)
-
장점 : (상대적으로) 적은 수의 parameter 만 사용해도 OK … overfitting 방지
-
ex) 제곱, 루트, 로그, 차분
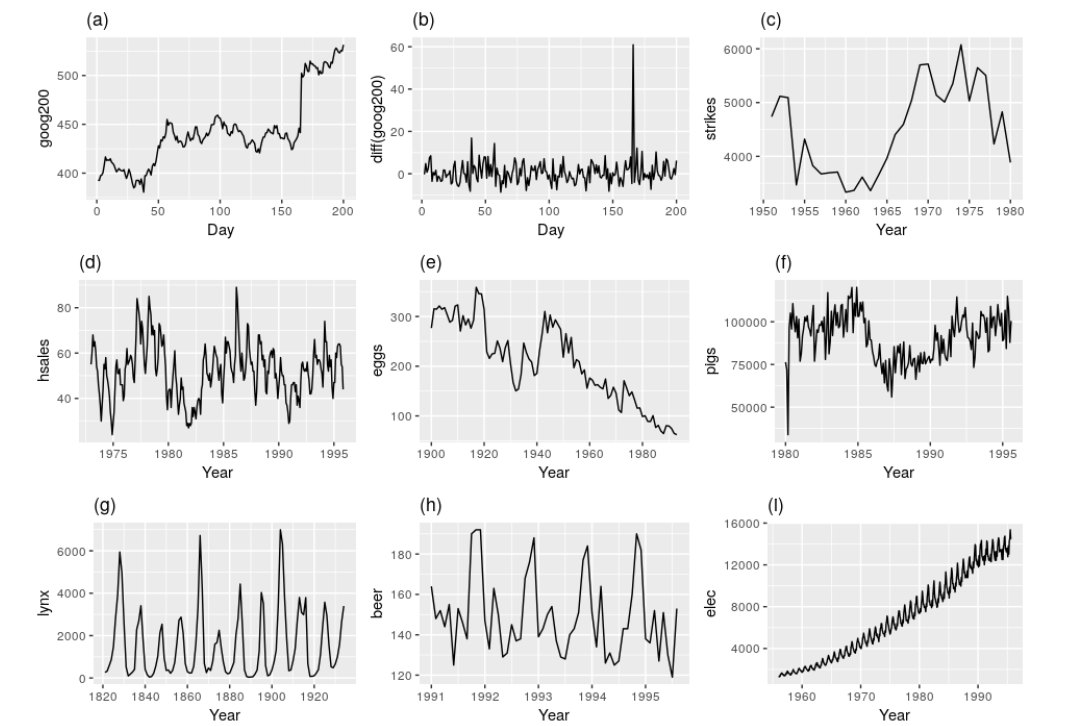
- 추세(Trend) 있는 거 : (a),(c),(e),(f),(i)
- 계절성(Seasonality) 있는 거 : (d), (h), (i)
- 주기(Cycle) 있는 거 : (g)
- 이분산성 : (i)
아래의 모든 방법들은 모두 어떻게 하면 정상성을 갖춘 시계열 데이터로 변환할까?에 대한 방법들이다.
(1) Log Transformation ( 로그 변환 )
WHEN? 시간 갈 수록 분산 증가
- 로그 변환 후, 분산이 일정해지면 “추세 제거” 가능! 그런 뒤 정상 과정으로 모델링 OK
(a) 기존 분포
- \(\text{E}(Y_t) = \mu_t = f(t)\).
- \(\sqrt{\text{Var}(Y_t)} = \mu_t \sigma\).
(b) 로그 변환 후 분포
- \(Y_t = Y_{t-1} + Y_t - Y_{t-1}\).
- \(\dfrac{Y_t}{Y_{t-1}} = 1 + \dfrac{Y_t - Y_{t-1}}{Y_{t-1}}\).
- \(log(\dfrac{Y_t}{Y_{t-1}}) = log(1 + \dfrac{Y_t - Y_{t-1}}{Y_{t-1}}) \approx \dfrac{Y_t - Y_{t-1}}{Y_{t-1}}\).
- \(log(Y_t) - log(Y_{t-1}) \approx \dfrac{Y_t - Y_{t-1}}{Y_{t-1}}\).
따라서..
- \(\text{E}(\log Y_t) = \log \mu_t\).
- \(\text{Var}(\log Y_t) \approx \sigma^2\).
(c) Generalization of Return
- \(R_t = \dfrac{Y_{t}}{Y_{t-1}} - 1\).
- \(\log{Y_t} - \log{Y_{t-1}} = \log{(R_t + 1)} \approx R_t \;\; \text{ if } \mid R_t \mid < 0.2\).
(2) Difference ( 차분 )
- (A) 계절성 제거
- (B) 추세 제거
(a) 계절성 제거
- “특정한 달/요일에 따라 기대값이 달라지는 것”
- 변수 더미화를 통해 추정 가능
[ 제거 방법 1 ] 계절성 추정(\(f(t)\)) 후 계절성 제거!
-
계절변수 더미화를 통해 기댓값 함수 ( = \(f(t)\) ) 를 알아내기
-
\(Y_t\) = \(f(t)\) + \(Y^s_t\)
where \(f(t) = \sum_{i=0}^{\infty} a_i D_i = a_0 + a_1 D_1 + a_2 D_2 + \cdots\)
( 여기서 \(D\) 는 더미변수 )
[ 제거 방법 2 ] 차분 적용 \((1-L^d) Y_t\) 후 계절성 제거!
if \(d=1\)
\[\begin{align*} Y_t &=> (1-L^1) Y_t \\ &= (1-Lag^1) Y_t \\ &= Y_t - Lag^1(Y_t) \\ &= Y_t - Y_{t-1} \\\end{align*}\]
if \(d=2\)
\(\begin{align*}Y_t &=> (1-L^2) Y_t \\ &= (1-Lag^2) Y_t \\ &= Y_t - Lag^2(Y_t) \\ &= Y_t - Y_{t-2} \\ \end{align*}\).
(b) 추세 제거
[ 제거 방법 1 ] 추세 추정(\(f(t)\)) 후 계절성 제거!
-
\(Y_t = f(t) + Y^s_t\).
where \(f(t) = \sum_{i=0}^{\infty} a_i t^i = a_0 + a_1 t + a_2 t^2 + \cdots\)
[ 제거 방법 2 ] 차분 적용 \((1-L^1)^d Y_t\) 후 추세 제거!
if \(d=1\)
\(\begin{align*} Y_t &=> (1-L^1)^1 Y_t \\ &= (1-Lag^1)^1 Y_t \\ &= Y_t - Lag^1(Y_t) \\ &= Y_t - Y_{t-1} \\ \end{align*}\).
if \(d=2\)
\(\begin{align*} Y_t &=> (1-L^1)^2 Y_t \\ &= (1-2L^1+L^2) Y_t \\ &= (1-2Lag^1+Lag^2) Y_t \\ &= Y_t - 2Lag^1(Y_t) + Lag^2(Y_t) \\ &= Y_t - Lag^1(Y_t) - Lag^1(Y_t) + Lag^2(Y_t) \\ &= (Y_t - Lag^1(Y_t)) - (Lag^1(Y_t) - Lag^2(Y_t)) \\ &= (Y_t - L^1(Y_t)) - (L^1(Y_t) - L^2(Y_t)) \\ &= (Y_t - Y_{t-1}) - (Y_{t-1} - Y_{t-2}) \\ &= Y_t - 2Y_{t-1} + Y_{t-2} \\ \end{align*}\).
(c) Box-Cox Transformation
-
비정규분포 \(\rightarrow\) 정규분포
-
모수(parameter) \(\lambda\)를 가짐
( 다양한 \(\lambda\) 값을 시도후, 가장 정규성을 높여주는 값 사용 )
-
\(\begin{align*} y^{(\boldsymbol{\lambda})} = \begin{cases} \dfrac{y^{\lambda} - 1}{\lambda} & \text{if } \lambda \neq 0, \\ \ln{y} & \text{if } \lambda = 0, \end{cases} \end{align*}\).
3. 비정상성 \(\rightarrow\) 정상성 test
(1) 추세 & (2) 계절성이 모두 제거된 정상성 데이터인가?
- ( for (1) 추세 제거 check ) ADF 정상성 확인
- ( for (2) 계절성 제거 check ) KPSS 정상성 확인
4. 실습
(1) 추세 제거
a) import packages & dataset
import pandas as pd
from statsmodels import datasets
import matplotlib.pyplot as plt
import statsmodels.api as sm
from module import stationarity_adf_test, stationarity_kpss_test
raw_set = datasets.get_rdataset("CO2", package="datasets")
raw = raw_set.data
b) 현재 데이터 확인
plt.plot(raw.time, raw.value)
plt.show()
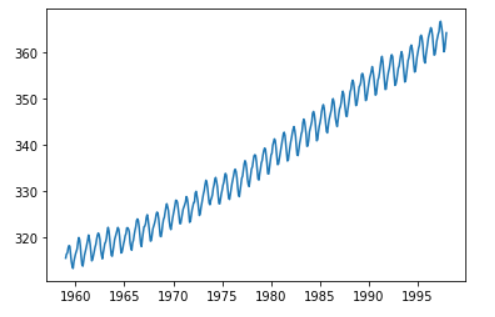
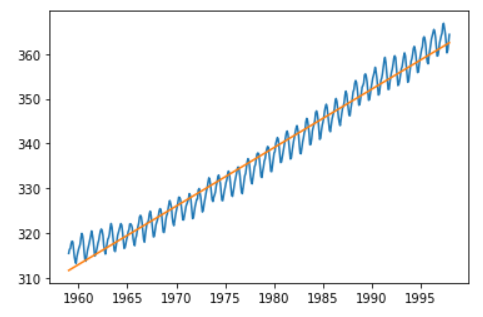
c) 모델 fitting & 추세 확인 ( 선형 )
result = sm.OLS.from_formula(formula='value~time', data=raw).fit()
trend = result.params[0] + (result.params[1] * raw.time)
plt.plot(raw.time, raw.value, raw.time, trend)
plt.show()
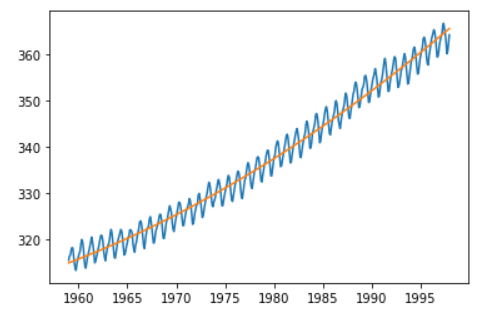
d) 모델 fitting & 추세 확인 ( 비선형 )
result = sm.OLS.from_formula(formula='value~time+I(time**2)', data=raw).fit()
trend = result.params[0] + result.params[1] * raw.time + result.params[2] * raw.time**2
plt.plot(raw.time, raw.value, raw.time, trend)
plt.show()
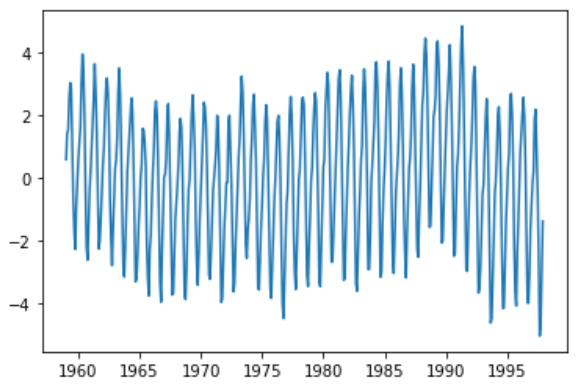
e) 잔차 확인
plt.plot(raw.time, result.resid)
plt.show()
ACF plot 확인
sm.graphics.tsa.plot_acf(result.resid, lags=100, use_vlines=True)
plt.tight_layout()
plt.show()
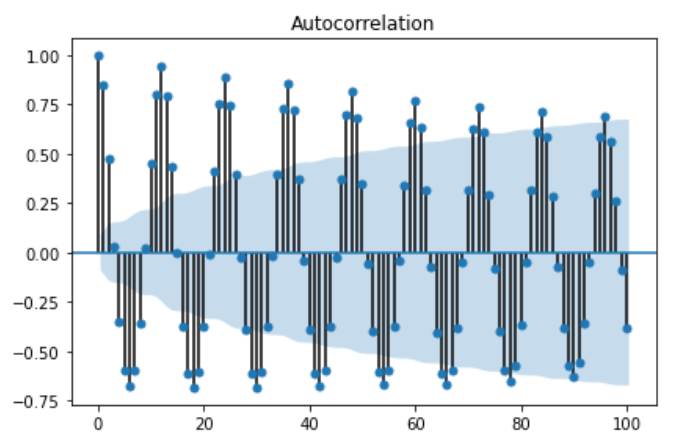
- 파란색 음영 내부에 있으면 autocorrelation이 없다고 판단
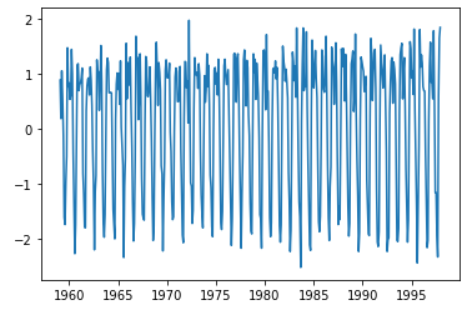
f) 추세 제거 ( with 차분 )
plt.plot(raw.time[1:], raw.value.diff(1).dropna())
plt.show()
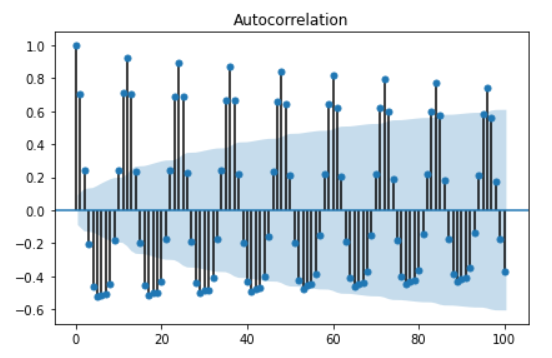
ACF plot 확인
sm.graphics.tsa.plot_acf(raw.value.diff(1).dropna(), lags=100, use_vlines=True)
plt.tight_layout()
plt.show()
(2) 계절성 제거
a) import packages & dataset
import pandas as pd
from statsmodels import datasets
import matplotlib.pyplot as plt
import statsmodels.api as sm
from module import stationarity_adf_test, stationarity_kpss_test
raw_set = datasets.get_rdataset("deaths", package="MASS")
raw = raw_set.data
b) 시간변수 추출
raw.time = pd.date_range('1974-01-01', periods=len(raw), freq='M')
raw['month'] = raw.time.dt.month
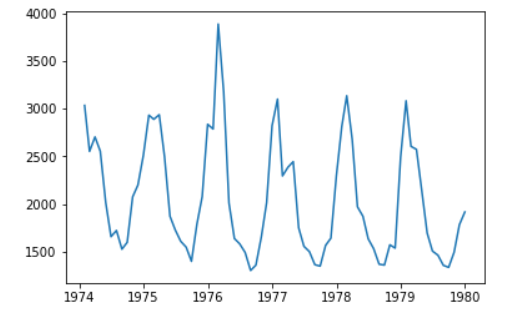
c) 현재 데이터 확인
plt.plot(raw.time, raw.value)
plt.show()
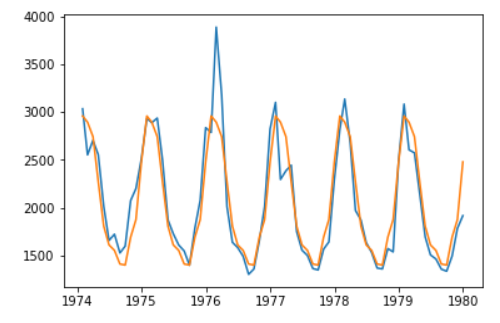
d) 모델 fitting & 예측값 확인
result = sm.OLS.from_formula(formula='value ~ C(month) - 1', data=raw).fit()
plt.plot(raw.time, raw.value, raw.time, result.fittedvalues)
plt.show()
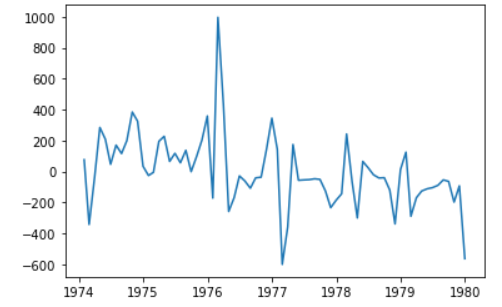
e) 잔차 확인
plt.plot(raw.time, result.resid)
plt.show()
ACF plot 확인
sm.graphics.tsa.plot_acf(result.resid, lags=50, use_vlines=True)
plt.tight_layout()
plt.show()
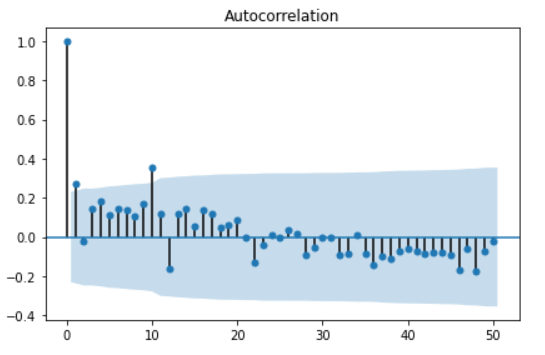
- 파란색 음영 내부에 있으면 autocorrelation이 없다고 판단
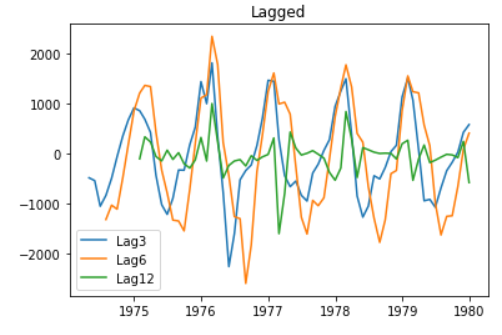
f) 계절성 제거 ( with 차분 )
seasonal_lag = 3
plt.plot(raw.time[seasonal_lag:], raw.value.diff(seasonal_lag).dropna(), label='Lag{}'.format(seasonal_lag))
seasonal_lag = 6
plt.plot(raw.time[seasonal_lag:], raw.value.diff(seasonal_lag).dropna(), label='Lag{}'.format(seasonal_lag))
seasonal_lag = 12
plt.plot(raw.time[seasonal_lag:], raw.value.diff(seasonal_lag).dropna(), label='Lag{}'.format(seasonal_lag))
plt.title('Lagged')
plt.legend()
plt.show()
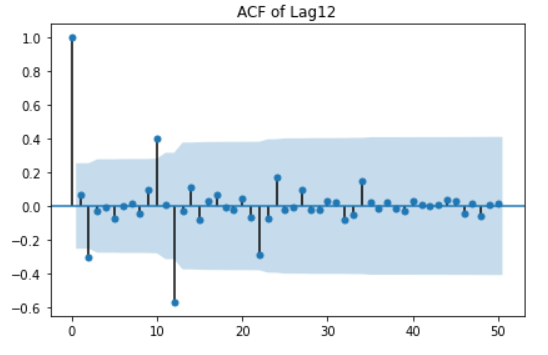
ACF plot 확인 ( lag=12인 경우 )
seasonal_lag = 12
sm.graphics.tsa.plot_acf(raw.value.diff(seasonal_lag).dropna(), lags=50,
use_vlines=True, title='ACF of Lag{}'.format(seasonal_lag))
plt.tight_layout()
plt.show()