(Forecasting ; Principles and Practice) 2.지수 평활

참고 : https://otexts.com/fppkr/

[ 지수 평활 ]

과거 관측값의 가중평균(weighted average)

• [part 1] 구체적인 작동 방식
• [part 2] 지수평활 기법의 기초를 이루는 통계적인 모델

1. 단순 지수 평활 ( simple exponential smoothing, SES )

단순 series

• 단순 기법 : \(\hat{y}_{T+h \mid T}=y_{T}\)

• 단순 평균 : \(\hat{y}_{T+h \mid T}=\frac{1}{T} \sum_{t=1}^{T} y_{t}\)

• 단순 지수 평활 : \(\hat{y}_{T+1 \mid T}=\alpha y_{T}+\alpha(1-\alpha) y_{T-1}+\alpha(1-\alpha)^{2} y_{T-2}+\cdots\)

  • \(0 \leq \alpha \leq 1\) : 평활 매개 변수
    • 클수록, 최근에 더 가중치
    • 작을수록, uniform

2가지 표현 방법

• 1) 가중 평균 형태
• 2) 성분 형태

1) 가중 평균 형태

• 시간 \(T+1\)에 대한..

  • 예측값 : \(\hat{y}_{T \mid T-1}\)
  • 관측값 : \(y_{T}\)

• 예측값 : \(\hat{y}_{T+1 \mid t}=\alpha y_{T}+(1-\alpha) \hat{y}_{T \mid T-1}\)

  • \(\hat{y}_{T+1 \mid T}=\sum_{j=0}^{T-1} \alpha(1-\alpha)^{j} y_{T-j}+(1-\alpha)^{T} \ell_{0}\).

    where \(l_0\) : 첫 번째 fitted value

2) 성분 형태

• 구성 : 각 성분에 대한 “예측식”과 ““평활식”“으로 구성

\[\begin{aligned} \text { Forecast equation } & \hat{y}_{t+h \mid t} =\ell_{t} \\ \text { Smoothing equation } & \ell_{t} =\alpha y_{t}+(1-\alpha) \ell_{t-1} \end{aligned}\]

• \(h=1\)일 경우, fitted value
• \(t=T\)일 경우, training data 이후의 예측값

평평한 예측값

\(\hat{y}_{T+h \mid T}=\hat{y}_{T+1 \mid T}=\ell_{T}, \quad h=2,3, \ldots\).

• 모든 예측값이 마지막 수준 성분과 같은 값
• 시계열에 추세나 계절 성분이 없을 때 사용

최적화

필요한 초기값 :

• 평활 매개변수 \(\alpha\)
• 초기 예측값 \(l_0\)

SSE로 풀기

• \(\mathrm{SSE}=\sum_{t=1}^{T}\left(y_{t}-\hat{y}_{t \mid t-1}\right)^{2}=\sum_{t=1}^{T} e_{t}^{2}\).

2. 추세 기법

(1) 홀트의 선형 추세 기법

( 단순 지수 평활 )

• (1개의) 예측식
• 1개의 평활식

\(\begin{aligned} \text { Forecast equation } & \hat{y}_{t+h \mid t} =\ell_{t} \\ \text { Smoothing equation } & \ell_{t} =\alpha y_{t}+(1-\alpha) \ell_{t-1} \end{aligned}\).

( 홀트의 선형 추세 기법 )

• (1개의) 예측식
• 2개의 평활식 ( 수준 (Level) & 추세 (Trend) )

\[\begin{aligned} \text { Forecast equation } & \hat{y}_{t+h \mid t} =\ell_{t}+h b_{t} \\ \text { Level equation } & \ell_{t} =\alpha y_{t}+(1-\alpha)\left(\ell_{t-1}+b_{t-1}\right) \\ \text { Trend equation } & b_{t} =\beta^{*}\left(\ell_{t}-\ell_{t-1}\right)+\left(1-\beta^{*}\right) b_{t-1} \end{aligned}\]

Summary

• \(l_t\) : \(t\) 시점에서의 “수준 추정 값”
  • \(0 \leq \alpha \leq 1\) : 수준에 대한 매개변수
• \(b_t\) : \(t\)시점에서의 “추세(기울기) 추정 값”
  • \(0 \leq \beta^{*} \leq 1\) : 추세(기울기)에 대한 매개변수

[ Level Equation ]

• (단순 지수 평활) \(\ell_{t} =\alpha y_{t}+(1-\alpha) \ell_{t-1}\)
• (홀트의 선형추세법) \(\ell_{t} =\alpha y_{t}+(1-\alpha)\left(\ell_{t-1}+b_{t-1}\right)\)
  • \(\ell_{t-1}+b_{t-1}\) = one-step-ahead training forecast ( 한 단계 앞선 예측 )

[ Trend Equation ]

\(b_{t} =\beta^{*}\left(\ell_{t}-\ell_{t-1}\right)+\left(1-\beta^{*}\right) b_{t-1}\).

• 1) 추세의 이전 추정 값 : \(\ell_t - \ell_{t-1}\)
• 2) 이전의 추세식 \(b_{t-1}\)

\(\rightarrow\) 이 둘의 가중 평균

(2) 감쇠 추세 기법 ( 감쇠 홀트(damped Holt) 기법 )

• 홀트(Holt)의 선형 기법으로 얻은 예측값은 미래에도 계속 일정한 (증가 또는 감소) 추세

\(\rightarrow\) 미래 어느 시점에 추세를 평평하게 감쇠시키는 한 가지 매개변수를 도입 ( \(0<\phi<1\) )

\(\begin{aligned} \hat{y}_{t+h \mid t} &=\ell_{t}+\left(\phi+\phi^{2}+\cdots+\phi^{h}\right) b_{t} \\ \ell_{t} &=\alpha y_{t}+(1-\alpha)\left(\ell_{t-1}+\phi b_{t-1}\right) \\ b_{t} &=\beta^{*}\left(\ell_{t}-\ell_{t-1}\right)+\left(1-\beta^{*}\right) \phi b_{t-1} . \end{aligned}\).

매개변수 \(\phi\)

• \(\phi=1\) : 홀트의 선형기법
• \(h \rightarrow \infty\) 일수록, 예측치는 \(\ell_{T}+\phi b_{T} /(1-\phi)\) 로 수렴
  • 단기 예측값은 “추세”
  • 장기 예측값은 “상수”
• \(\phi\)가 작을수록, “감쇠 효과 STRONG”
• 보통 \(\phi\)는 0.8~0.98

3. 홀트-윈터스의 계절성 기법

홀트-윈터스의 계절성 기법

• (1개의) 예측식
• 3개의 평활식
  • \(\ell_t, b_t, s_t\) : 수준/추세/계절성분
  • \(\alpha, \beta^{*}, \gamma\) : 평활 매개 변수
  • \(m\) : 계절성의 주기
    • ex) 분기별 데이터 : \(m=4\), 월별 데이터 : \(m=12\)

2가지 변형

• 1) 덧셈 기법 : 계절성 변동이 시계열에 걸쳐 일정할 때
• 2) 곱셈 기법 : 계절성 변동이 시계열에 걸쳐 비례할 때

(1) 덧셈 기법

\(\begin{aligned} \hat{y}_{t+h \mid t} &=\ell_{t}+h b_{t}+s_{t+h-m(k+1)} \\ \ell_{t} &=\alpha\left(y_{t}-s_{t-m}\right)+(1-\alpha)\left(\ell_{t-1}+b_{t-1}\right) \\ b_{t} &=\beta^{*}\left(\ell_{t}-\ell_{t-1}\right)+\left(1-\beta^{*}\right) b_{t-1} \\ s_{t} &=\gamma\left(y_{t}-\ell_{t-1}-b_{t-1}\right)+(1-\gamma) s_{t-m} \end{aligned}\).

[ Level Equation ]

\(\ell_{t} =\alpha\left(y_{t}-s_{t-m}\right)+(1-\alpha)\left(\ell_{t-1}+b_{t-1}\right)\).

• 1) 계절성으로 조정된 관측값 : \(y_t - s_{t-m}\)
• 2) 시간 \(t\)에 대한 “비계절성 예측” : \(\ell_{t-1}+b_{t-1}\)

[ Trend Equation ]

• 홀트의 선형기법과 동일

[ Seasonality Equation ]

\(s_{t} =\gamma\left(y_{t}-\ell_{t-1}-b_{t-1}\right)+(1-\gamma) s_{t-m}\).

• 1) 현재 계절성 지수 : \(y_{t}-\ell_{t-1}-b_{t-1}\)
• 2) 이전 년도 같은 계절 (=\(m\)시전 이전)의 계절성 지표 : \(s_{t-m}\)

(2) 곱셈 기법

• 곱셈이라 해서, “모든게 곱셈”이 아니라, “계절성이 곱셈”인 것

\(\begin{aligned} \hat{y}_{t+h \mid t} &=\left(\ell_{t}+h b_{t}\right) s_{t+h-m(k+1)} \\ \ell_{t} &=\alpha \frac{y_{t}}{s_{t-m}}+(1-\alpha)\left(\ell_{t-1}+b_{t-1}\right) \\ b_{t} &=\beta^{*}\left(\ell_{t}-\ell_{t-1}\right)+\left(1-\beta^{*}\right) b_{t-1} \\ s_{t} &=\gamma \frac{y_{t}}{\left(\ell_{t-1}+b_{t-1}\right)}+(1-\gamma) s_{t-m} \end{aligned}\).

(3) 홀트 윈터스의 감쇠 기법

( 곱셈 계절성 고려 시 )

\[\begin{aligned} \hat{y}_{t+h \mid t} &=\left[\ell_{t}+\left(\phi+\phi^{2}+\cdots+\phi^{h}\right) b_{t}\right] s_{t+h-m(k+1)} \\ \ell_{t} &=\alpha\left(y_{t} / s_{t-m}\right)+(1-\alpha)\left(\ell_{t-1}+\phi b_{t-1}\right) \\ b_{t} &=\beta^{*}\left(\ell_{t}-\ell_{t-1}\right)+\left(1-\beta^{*}\right) \phi b_{t-1} \\ s_{t} &=\gamma \frac{y_{t}}{\left(\ell_{t-1}+\phi b_{t-1}\right)}+(1-\gamma) s_{t-m} . \end{aligned}\]

4. 지수 평활 기법의 분류 쳬계

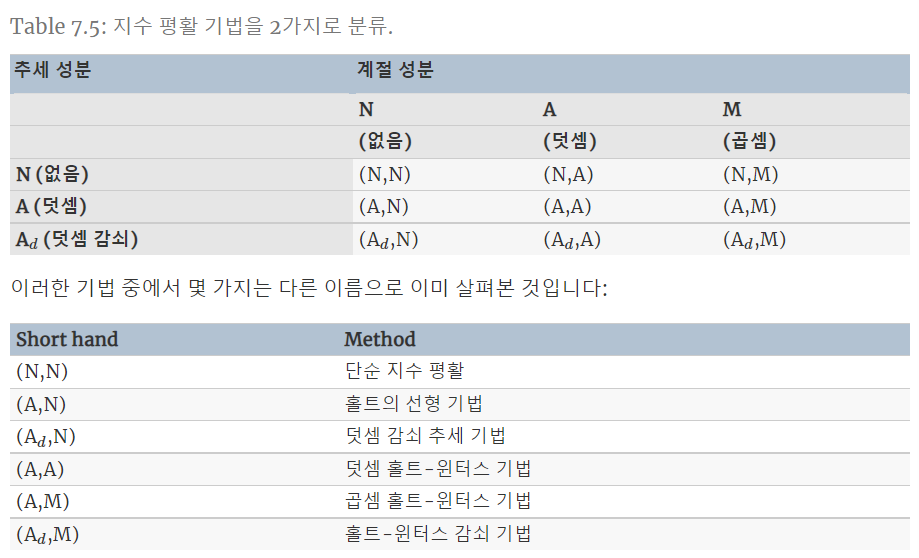
5. 상태 공간 모델 (State Space Models, SSM)

지수 평활 기법에 깔린 통계적인 모델

각 모델은 2가지로 구성

• 1) 측정식 ( measurement equation ) : 관측 O
• 2) 상태식 ( state equation ) : 관측 X

각 기법마다, 2가지 모델 존재

• 1) 덧셈 오차
• 2) 곱셈 오차

이를 구분하기 위해, 세 번째 문자 하나 추가

SSM의 표기법

• ETS = Exponential Smoothing
• ETS(\(\cdot, \cdot, \cdot\)) : 각각 Error/Trend/Seasonal

(1) ETS(A,N,N)

ETS(A,N,N) = “덧셈 오차”를 이용하는 “단순 지수 평활”

• Error : Additive
• Trend : X
• Seasonal : X

단순 지수 평활

• Forecast equation : \(\hat{y}_{t+1 \mid t}=\ell_{t}\)

• Level (Smoothing) equation : \(\ell_{t}=\alpha y_{t}+(1-\alpha) \ell_{t-1}\)

Level Equation 재정리

• before ) \(\ell_{t}=\alpha y_{t}+(1-\alpha) \ell_{t-1}\)
• after ) \(\ell_{t}=\alpha y_{t}+(1-\alpha)e_t\)
  • since \(e_{t}=y_{t}-\ell_{t-1}=y_{t}-\hat{y}_{t \mid t-1}\)

각 관측값이 이전 수준에 오차를 더한 것과 같게 두기 위해…

• \(y_t = \ell_{t-1} + e_t\)…. where \(e_{t}=\varepsilon_{t} \sim \operatorname{NID}\left(0, \sigma^{2}\right)\)
• 다시 쓰면,
  • \(y_{t}=\ell_{t-1}+\varepsilon_{t}\).
  • \(\ell_{t}=\ell_{t-1}+\alpha \varepsilon_{t}\).

(2) ETS(M,N,N)

ETS(M,N,N) = “곱셈 오차”를 이용한 “단순 지수 평활”

곱셈 오차 : \(\varepsilon_{t}=\frac{y_{t}-\hat{y}_{t \mid t-1}}{\hat{y}_{t \mid t-1}}\)….. where \(\varepsilon_{t} \sim \operatorname{NID}\left(0, \sigma^{2}\right)\)

\(\begin{aligned} y_{t} &=\ell_{t-1}\left(1+\varepsilon_{t}\right) \\ \ell_{t} &=\ell_{t-1}\left(1+\alpha \varepsilon_{t}\right) . \end{aligned}\).

(3) ETS(A,A,N)

ETS(A,A,N) = “덧셈 오차”를 이용한 “홀트의 선형 기법”

덧셈 오차 : \(\varepsilon_{t}=y_{t}-\ell_{t-1}-b_{t-1} \sim \mathrm{NID}\left(0, \sigma^{2}\right)\)

\(\begin{aligned} &y_{t}=\ell_{t-1}+b_{t-1}+\varepsilon_{t} \\ &\ell_{t}=\ell_{t-1}+b_{t-1}+\alpha \varepsilon_{t} \\ &b_{t}=b_{t-1}+\beta \varepsilon_{t} \end{aligned}\).

(4) ETS(M,A,N)

ETS(M,A,N) = “곱셈 오차”를 이용한 “홀트의 선형 기법”

곱셈 오차 : \(\varepsilon_{t}=\frac{y_{t}-\left(\ell_{t-1}+b_{t-1}\right)}{\left(\ell_{t-1}+b_{t-1}\right)}\)…… where \(\varepsilon_{t} \sim \operatorname{NID}\left(0, \sigma^{2}\right)\)

\(\begin{aligned} y_{t} &=\left(\ell_{t-1}+b_{t-1}\right)\left(1+\varepsilon_{t}\right) \\ \ell_{t} &=\left(\ell_{t-1}+b_{t-1}\right)\left(1+\alpha \varepsilon_{t}\right) \\ b_{t} &=b_{t-1}+\beta\left(\ell_{t-1}+b_{t-1}\right) \varepsilon_{t} \end{aligned}\).

• 간결성을 위해, \(\beta=\alpha \beta^{*}\)