참고 : https://otexts.com/fppkr/
[ 계층적/그룹화된 시계열 ]
Ex) 자전거 판매 수
- 산악 자전거
- 로드 바이크
- 어린이용 자전거
- …
시계열 모음(collection)은 계층적인 합산 구조(hierarchical aggregation structure)를 따름
\(\rightarrow\) 계층적 시계열(hierarchical time series)
- ex) 지역-주-매장
제품 종류와 지리적인 위치를 동시에 고려하여 분배(disaggregate) 가능
\(\rightarrow\) 그룹화된 시계열 (grouped time series)
1. 계층적 시계열
ex) \(K=2\) 수준 계층 구조
- 수준 0 : TOTAL …. 수준 2 : 가장 하단
- Notation : \(y_{j.t}\)
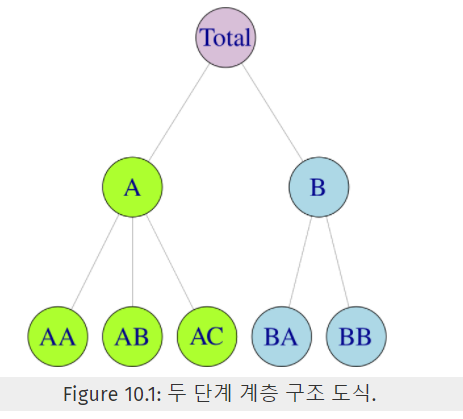
\(y_{t}=y_{\mathrm{AA}, t}+y_{\mathrm{AB}, t}+y_{\mathrm{AC}, t}+y_{\mathrm{BA}, t}+y_{\mathrm{BB}, t}\).
- \(y_{\mathrm{A}, t}=y_{\mathrm{AA}, t}+y_{\mathrm{AB}, t}+y_{\mathrm{AC}, t}\).
- \(y_{\mathrm{B}, t}=y_{\mathrm{BA}, t}+y_{\mathrm{BB}, t}\).
Matrix Formulation
-
\(\boldsymbol{y}_{t}=\boldsymbol{S} \boldsymbol{b}_{t}\).
-
\(S\) : 합산 행렬 (summing matrix)
\(\left[\begin{array}{c} y_{t} \\ y_{\mathrm{A}, t} \\ y_{\mathrm{B}, t} \\ y_{\mathrm{AA}, t} \\ y_{\mathrm{AB}, t} \\ y_{\mathrm{AC}, t} \\ y_{\mathrm{BA}, t} \\ y_{\mathrm{BB}, t} \end{array}\right]=\left[\begin{array}{ccccc} 1 & 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 & 1 \\ 1 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 1 \end{array}\right]\left[\begin{array}{c} y_{\mathrm{AA}, t} \\ y_{\mathrm{AB}, t} \\ y_{\mathrm{AC}, t} \\ y_{\mathrm{BA}, t} \\ y_{\mathrm{BB}, t} \end{array}\right]\).
2. 그룹화된 시계열
계층적 시계열보다 더 일반적인 합산 구조
ex) \(K=2\)-수준 그룹화된 구조
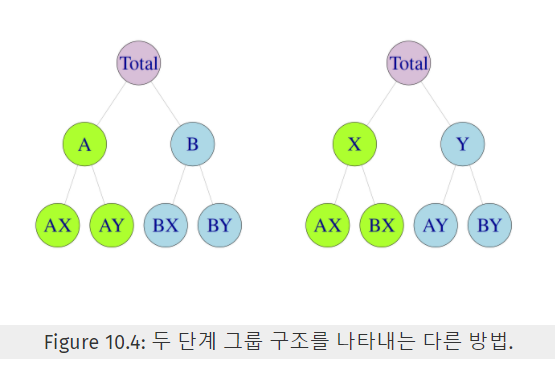
\(y_{t}=y_{\mathrm{AX}, t}+y_{\mathrm{AY}, t}+y_{\mathrm{BX}, t}+y_{\mathrm{BY}, t}\).
- 표현 방법 1)
- \(y_{\mathrm{A}, t}=y_{\mathrm{AX}, t}+y_{\mathrm{AY}, t}\).
- \(y_{\mathrm{B}, t}=y_{\mathrm{BX}, t}+y_{\mathrm{BY}, t}\).
- 표현 방법 2)
- \(y_{\mathrm{X}, t}=y_{\mathrm{AX}, t}+y_{\mathrm{BX}, t}\).
- \(y_{\mathrm{Y}, t}=y_{\mathrm{AY}, t}+y_{\mathrm{BY}, t}\).
\(\left[\begin{array}{c} y_{t} \\ y_{\mathrm{A}, t} \\ y_{\mathrm{B}, t} \\ y_{\mathrm{X}, t} \\ y_{\mathrm{Y}, t} \\ y_{\mathrm{AX}, t} \\ y_{\mathrm{AY}, t} \\ y_{\mathrm{BX}, t} \\ y_{\mathrm{BY}, t} \end{array}\right]=\left[\begin{array}{llll} 1 & 1 & 1 & 1 \\ 1 & 1 & 0 & 0 \\ 0 & 0 & 1 & 1 \\ 1 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 \\ 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{array}\right]\left[\begin{array}{c} y_{\mathrm{AX}, t} \\ y_{\mathrm{AY}, t} \\ y_{\mathrm{BX}, t} \\ y_{\mathrm{BY}, t} \end{array}\right]\).
3. 상향식 접근 방식
\(\begin{aligned} \tilde{y}_{h} &=\hat{y}_{\mathrm{AA}, h}+\hat{y}_{\mathrm{AB}, h}+\hat{y}_{\mathrm{AC}, h}+\hat{y}_{\mathrm{BA}, h}+\hat{y}_{\mathrm{BB}, h}, \\ \tilde{y}_{\mathrm{A}, h} &=\hat{y}_{\mathrm{AA}, h}+\hat{y}_{\mathrm{AB}, h}+\hat{y}_{\mathrm{AC}, h}, \\ \text { and } \tilde{y}_{\mathrm{B}, h} &=\hat{y}_{\mathrm{BA}, h}+\hat{y}_{\mathrm{BB}, h} . \end{aligned}\).
\(\tilde{\boldsymbol{y}}_{h}=\boldsymbol{S} \hat{\boldsymbol{b}}_{h}\).
\(\left[\begin{array}{c}\tilde{y}_{h} \\ \tilde{y}_{\mathrm{A}, h} \\ \tilde{y}_{\mathrm{AA}, h} \\ \tilde{y}_{\mathrm{AB}, h} \\ \tilde{y}_{\mathrm{AC}, h} \\ \tilde{y}_{\mathrm{BA}, h} \\ \tilde{y}_{\mathrm{BB}, h}\end{array}\right]=\left[\begin{array}{ccccc}1 & 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 & 1 \\ 1 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 1\end{array}\right]\left[\begin{array}{c}\hat{y}_{\mathrm{AA}, h} \\ \hat{y}_{\mathrm{AB}, h} \\ \hat{y}_{\mathrm{AC}, h} \\ \hat{y}_{\mathrm{BA}, h} \\ \hat{y}_{\mathrm{BB}, h}\end{array}\right]\).
4. 하향식 접근 방법
\(p_1, \cdots p_m\) :
- 시계열의 예측값이 어떻게 분배되는지 나타내는 분배비율(disaggregation proportion)의 집합
- \(\tilde{\boldsymbol{b}}_{t}=\boldsymbol{p} \hat{y}_{t}\).
- \(\tilde{\boldsymbol{y}}_{h}=\boldsymbol{S} \boldsymbol{p} \hat{y}_{t}\).
(1) 과거 “비율값”을 평균
top-down Gross-Sohl method A
\(p_{j}=\frac{1}{T} \sum_{t=1}^{T} \frac{y_{j, t}}{y_{t}}\).
(2) 과거 “평균값”의 비율
top-down Gross-Sohl method F
\(p_{j}=\sum_{t=1}^{T} \frac{y_{j, t}}{T} / \sum_{t=1}^{T} \frac{y_{t}}{T}\).
(3) 예측 비율값
위의 2 방법은, 비율이 시간에 따라서 변할 수도 있다는 것을 고려하지 못하기 때문에!
\(\rightarrow\) (과거 비율에 근거한) 하향식 접근 방식 < 상향식 접근 방식
(생략)
