AAA (All About AI)

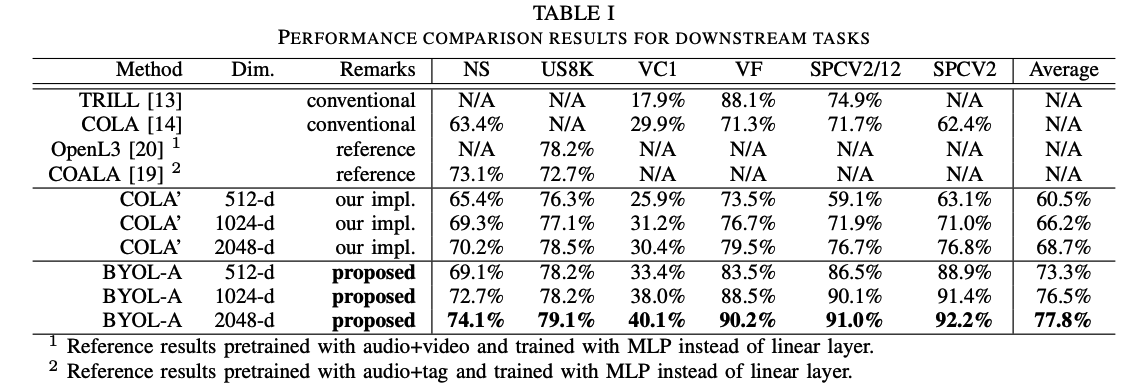
BYOL for Audio: Self-Supervised Learning for General-Purpose Audio Representation (IJCNN, 2021)

https://arxiv.org/pdf/2103.06695.pdf

Contents

1. Abstract
2. Introduction
3. BYOL-A

   1. Pre-normalization

   2. Mixup for foreground acoustic event

   3. RRC for all content details

   4. Post-Normalization

4. Experiments

Abstract

New general-purpose audio representation learning approach!

No negatives samples ( \(\approx\) BYOL )

• without expecting relationships between different time segments of audio samples.

Bootstrap Your Own Latent (BYOL) for Audio (BYOL-A)

• creates contrasts in an augmented audio segment pair derived from a single audio segment
• combination of normalization and augmentation techniques

1. Introduction

Contrastive Learning

• use positive and negative samples
• requires a large number of negative samples
  • SimCLR [7] : uses a significant number of batch samples
  • MoCo [6] : operates a large queue to accommodate a larger number of negative samples.
  • BYOL [8] : does not use negative samples

Bootstrap Your Own Latent (BYOL)

• no negative samples

• directly minimizes the MSE of embeddings originating from the same input
• collapsed representations? system architecture and training algorithm can avoid this problem!

SSL in Audio

COLA [14]: learns general-purpose representations and outperforms previous methods

Others: utilize the time-series aspect of audio signals

• audio segments cropped closer = closer representations (?)

  \(\rightarrow\) contradictory use cases can be found easily!

  • ex) repetitive sounds like music could have similar contents in the remote time segments because music compositions, by their nature, repeat motifs.

  ex) short acoustic events (e.g., a single knock, a gunshot) can occur in a short duration

  • even adjacent segments (e.g., a knock followed by a footstep) can make differences in contents for acoustic events.

• similar problems can also happen when we use contrastive learning [11] [14] or triplet loss [12] [13] because the comparison of multiple samples is the core of their loss calculation.

BYOL-A

Address these problems by having general-purpose audio representations , learned from a single audio segment!!

Focus on learning

• (A) the foreground acoustic event sound as a dominant sound representation

• (B) the sound texture details

for describing general-purpose representation.

(A) Foreground acoustic event

• Can be better learned from samples with random background variations while the foreground is kept unchanged

• mixing small amount of sounds can approximate making variations on the background.

  \(\rightarrow\) adopt “mixup”

(B) Sound texture

• Sounds from an acoustic scene or a sound texture can vary their pitch/speed/time, while the details can be consistent

• details can be learned under the random variations of pitch/speed/time shifts

  \(\rightarrow\) use approximation of audio “pitch shifting” and “time stretching” techniques

Create changes on a pair of segments originating from exactly the same segment, not from multiple segments

Contributions

• (1) Propose learning general-purpose audio representations from a single audio segment
• (2) BYOL for Audio (BYOL-A)
  • learns representations from a single audio segment input with a dedicated audio augmentation module that focuses on foreground and content details
• (3) Propose to learn ..
  • a) foreground sound by combining pre-normalization and mixup
  • b) content details through approximation of pitch shifting and time stretching.
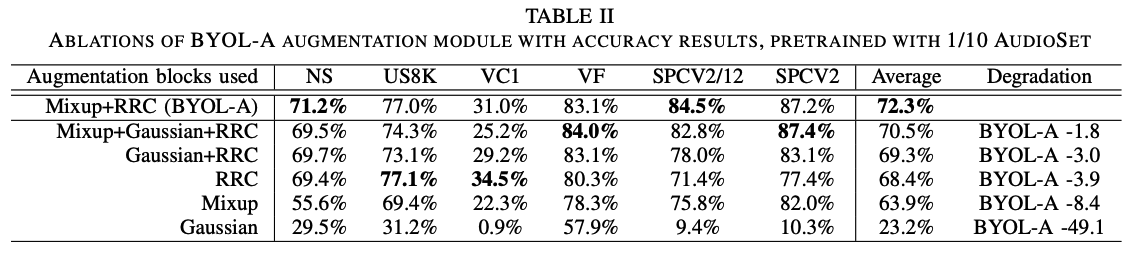
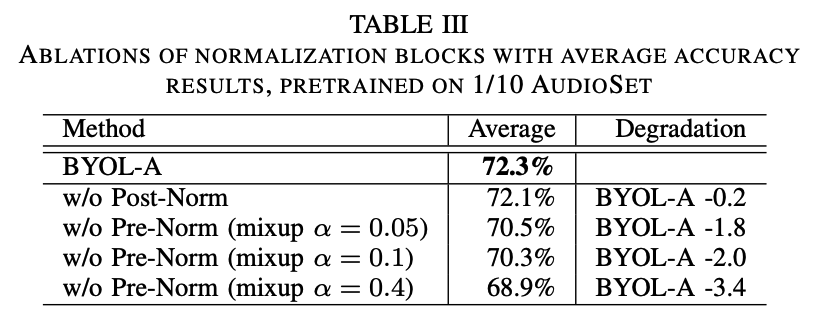
• (4) Extensive ablation studies

2. BYOL-A

General-purpose audio representations from a single audio segment

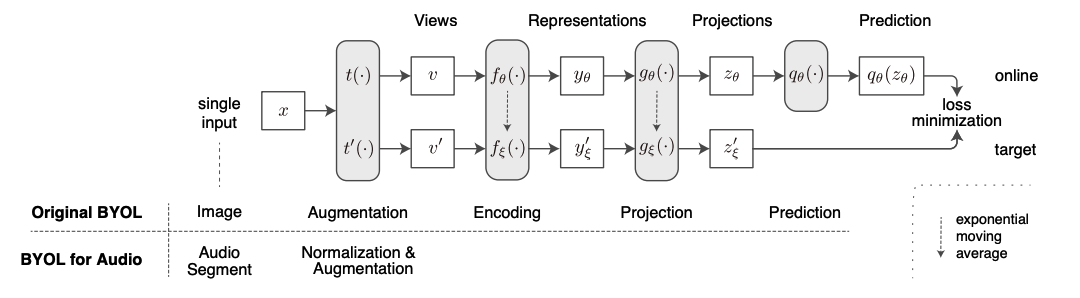
(1) Input : audio preprocessed as a log-scaled mel-spectrogram ( = time frequency feature )

(2) Data Augmentation: replace the augmentation module in BYOL with ours

• so that the learning system can handle audio and create contrasts in augmented views

• augmentation module consists of 4 blocks

• 

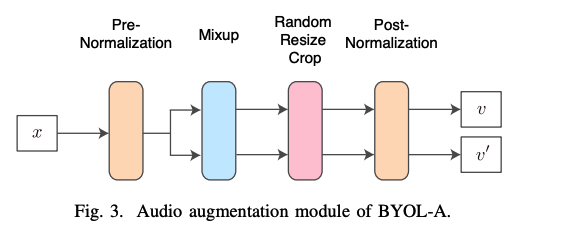
Data Augmentation blocks

• (1) Pre-Normalization block

  • normalizes a single input audio segment ( for stability )

  • normalized input is duplicated into 2copies

• (2) Mixup block : creates two outputs that are mixes of ..

  • a) normalized inputs & b) randomly chosen past normalized inputs.
  • designed to create contrast for learning foreground acoustic event representations,

• (3) Random Resize Crop (RRC) block

  • resizes and crops the outputs randomly
  • approximates pitch shifting and time stretching in time-frequency features

• (4) Post-Normalization block

  • adjusts statistical drifts caused by the former augmentations
  • focus on foreground acoustic events and all content details.

(1) Pre-Normalization

• normalized to \(\tilde{x}=\frac{x-\mu}{\sigma}\),

• stabilizes computations in the system in two ways

  • (1) by mitigating augmentation parameter sensitivity
    • which enables following blocks to assume that input range virtually follows \(N(0,1)\).
  • (2) by normalizing statistical differences between training datasets.

(2) Mixup for foreground acoustic event

Input = normalized log-mel spectrogram audio

Mixup block

• mixes past randomly selected input audio in a small ratio

• added audio becomes a part of the background sound in the mixed audio.

  • similar to mixback [11], which adds a random sample from a dataset as background sound

    ( but the purpose of the mix-back is to create a set of positive samples sharing less information in the contrastive learning setting )

• Original mixup = to both X & Y

  BYOL-A = only to X

As audio is log-scaled, we convert input to a linear scale before the mixup calculation and convert it back to a log-scale again

\(\rightarrow\) coin as log-mixup-exp

\(\tilde{x}_i=\log \left((1-\lambda) \exp \left(x_i\right)+\lambda \exp \left(x_k\right)\right)\).

• \(x_k\) : mixing counterpart

• \(\lambda\) : mixing ratio sampled from uniform distribution \(U(0.0, \alpha)\)

  ( instead of from a beta distribution in the original mixup )

(3) RRC for all content details

approximation of pitch shifting and time stretching of input audio log-mel spectrograms

(4) Post-Normalization

After augmentation … can cause statistical drift in their outputs

\(\rightarrow\) Thus, normalize as \(\sim N(0,1)\).

Difference with pre-normalization?

• use BATCH statistics ( not INSTANCE-WISE )

3. Experiments