Pyg6

Chapter 6.

1) GAE (Graph Auto Encoder)

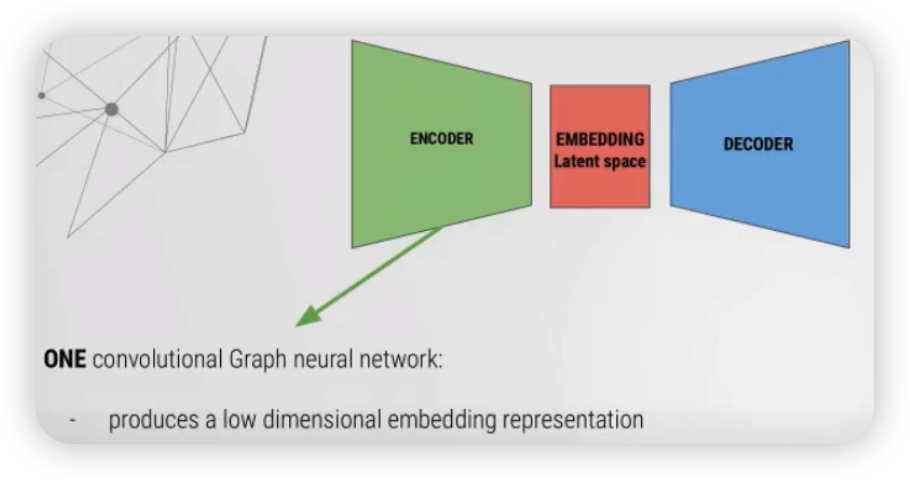
Encoder 부분 수식

• $Z = \bar{X}=G C N(A, X)=\operatorname{Re} L U\left(\tilde{A} X W_{0}\right)$,

  where $\tilde{A}=D^{-1 / 2} A D^{-1 / 2}$ ( = normalized adjacency matrix )

Example

아래와 같은 3개의 node가 있다고 해보자. ( A, B, C )

이것이 encoder를 통과해서, 각각 2차원의 노드로 임베딩되었다고 해보자.

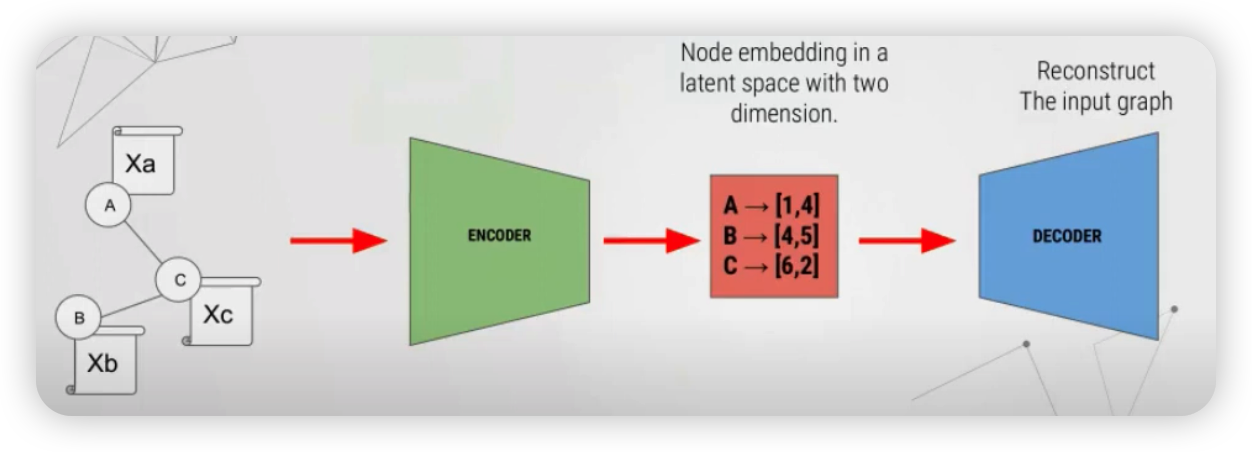
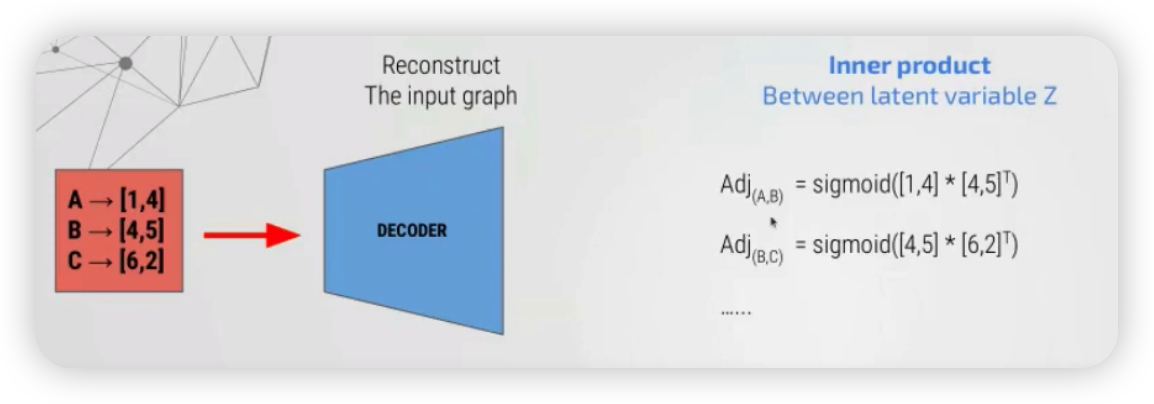
이렇게 임베딩된 3개의 2차원 벡터는, 다양한 방식을 통해 기존 그래프로 reconstruct될 수 있는데,

그 중 대표적인 방법은 단순히 inner product 한 뒤, sigmoid를 적용하는 것이다.

2) Import Dataset

dataset = Planetoid("\..", "CiteSeer", transform=T.NormalizeFeatures())
data = dataset[0]
data.train_mask = data.val_mask = data.test_mask = None
data = train_test_split_edges(data)

3) GAE의 Encoder

• 2개의 GCN을 인코더로써 사용할 것이다.
• activation function으로는 ReLU를 사용한다

class GCNEncoder(torch.nn.Module):
    def __init__(self, in_channels, out_channels):
        super(GCNEncoder, self).__init__() # cached only for transductive learning
        self.conv1 = GCNConv(in_channels, 2 * out_channels, cached=True)  
        self.conv2 = GCNConv(2 * out_channels, out_channels, cached=True) 
        
    def forward(self, x, edge_index):
        x = self.conv1(x, edge_index).relu()
        z = self.conv2(x, edge_index)
        return z

4) GAE

이번엔, torch_geometric에 있는 GAE 클래스를 사용할 것이다.

이 안에는, 위에서 우리가 생성한 GCNEncoder를 넣을 것이다.

from torch_geometric.nn import GAE

# parameters
out_channels = 2
num_features = dataset.num_features
epochs = 100

# model
model = GAE(GCNEncoder(num_features, out_channels))

device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
model = model.to(device)
x = data.x.to(device)
train_pos_edge_index = data.train_pos_edge_index.to(device)
optimizer = torch.optim.Adam(model.parameters(), lr=0.01)

5) train & test

참고로, GAE에서 reconstruction loss는 내장된 메소드인 model.recon_loss를 사용하면 된다.

• 이 손실함수는 아래의 2가지를 인자로 받는다
  • (1) embedding vector
  • (2) 정답값 ( = train_pos_edge_index )

def train():
    model.train()
    optimizer.zero_grad()
    z = model.encode(x, train_pos_edge_index)
    #-------------------------------------------------------#
    loss = model.recon_loss(z, train_pos_edge_index)
    #-------------------------------------------------------#
    loss.backward()
    optimizer.step()
    return float(loss)


def test(pos_edge_index, neg_edge_index):
    model.eval()
    with torch.no_grad():
        z = model.encode(x, train_pos_edge_index)
    return model.test(z, pos_edge_index, neg_edge_index)

6) GVAE ( Graph Variational AutoEncoder )

이번에는, AE 대신 VAE를 사용할 것이다.

이 둘의 차이점은, hidden representation $Z$가 deterministic하지 않고,

mean & var를 생성한 뒤, 이를 통해 샘플링 된 $Z$를 사용한다는 점이다.

( Loss Function에도 당연히 차이가 있다 )

수식 :

• $\log \sigma^{2}=G C N_{\sigma}(X, A)=\tilde{A} \bar{X} W_{1}$.

• $\mu=G C N_{\mu}(X, A)=\tilde{A} \bar{X} W_{1}$.

• $Z=\mu+\sigma \odot \epsilon$,

  where $\epsilon \sim N(0,1)$

모델 코드 ( 마지막에, 2개의 GCN layer를 사용 ( for mean & log std ) )

class VariationalGCNEncoder(torch.nn.Module):
    def __init__(self, in_channels, out_channels):
        super(VariationalGCNEncoder, self).__init__()
        self.conv1 = GCNConv(in_channels, 2 * out_channels, cached=True) 
        #---------------------------------------------------------------#
        self.conv_mu = GCNConv(2 * out_channels, out_channels, cached=True)
        self.conv_logstd = GCNConv(2 * out_channels, out_channels, cached=True)
        #---------------------------------------------------------------#

    def forward(self, x, edge_index):
        x = self.conv1(x, edge_index).relu()
        return self.conv_mu(x, edge_index), self.conv_logstd(x, edge_index)

train 코드 ( loss 부분에 변화 )

def train():
    model.train()
    optimizer.zero_grad()
    z = model.encode(x, train_pos_edge_index)
    #-------------------------------------------------------#
    loss = model.recon_loss(z, train_pos_edge_index)
    loss = loss + (1 / data.num_nodes) * model.kl_loss()
    #-------------------------------------------------------#
    loss.backward()
    optimizer.step()
    return float(loss)