Importance Weighting and Variational Inference (NeurIPS 2018)
Abstract
Using importance sampling ideas for better variational bounds
showing the resulting Importance Weighted Variational Inference (IWVI)
1. Introduction
Variational Inference
- \(\log p(\mathbf{x})=\underbrace{\underset{q(\mathbf{z})}{\mathbb{E}} \log \frac{p(\mathbf{z}, \mathbf{x})}{q(\mathbf{z})}}_{\operatorname{ELBO}[q(\mathbf{z}) \mid \mid p(\mathbf{z}, \mathbf{x})]}+\underbrace{\operatorname{KL}[q(\mathbf{z}) \mid \mid p(\mathbf{z} \mid \mathbf{x})]}_{\text {divergence }}\).
ELBO is closely related to Importance Sampling
-
for fixed \(q\), let \(R=p(\mathbf{z}, \mathbf{x}) / q(\mathbf{z})\) where \(\mathrm{z} \sim q\).
-
satisfies \(p(\mathrm{x})=\mathbb{E} R\)
-
by Jensen’s Inequality … \(\log p(\mathrm{x}) \geq \mathbb{E} \log R=\mathrm{ELBO}[q \mid \mid p]\)
- MC samples are used to estimate \(\mathbb{E} \log R\)
- yields a tighter bound, when \(R\) is more concentrated about its mean \(p(\mathbf{x})\)
-
\(R_{M}=\frac{1}{M} \sum_{m=1}^{M} R_{m}\).
-
\(\log p(\mathbf{x}) \geq \mathbb{E} \log R_{M}\) : “IW-ELBO”
\(\rightarrow\) IWVI = select \(q\) to maximize IW-ELBO
Contribution
- 1) provide new perspective on IWVI by highlighting a precise connection between IWVI and self-normalized importance sampling(NIS)
- 2) explore the connection between VI and IS by adapting the ideas of “defensive sampling”
2. Variational Inference
VI = simultaneously solving 2 problems
- 1) probabilistic inference : find \(q(\mathbf{z})\) close to \(p(\mathbf{z} \mid \mathbf{x})\)
- “Bayesian Inference”
- 2) bounding the marginal likelihood : finding a lower-bound on \(\log p(\mathrm{x})\).
- “Maximum Likelihood Learning”
3. Importance Weighting
use IS to obtain tighter ELBOs for learning VAEs!
Take any r.v. \(R\), such that \(\mathbb{E} R=p(\mathrm{x})\)
\(\rightarrow\) \(\log p(\mathbf{x})=\underbrace{\mathbb{E} \log R}_{\text {bound }}+\underbrace{\mathbb{E} \log \frac{p(\mathbf{x})}{R}}_{\text {looseness }}\)……. “generalization of ELBO”
- think of \(R\) as an “estimator” of \(p(x)\)
\(R=\omega(\mathbf{z})=\frac{p(\mathbf{z}, \mathbf{x})}{q(\mathbf{z})}, \mathbf{z} \sim q\).
-
obeys \(\mathbb{E} R=p(\mathrm{x})\)
-
then, (a) becomes (b)
- (a) \(\log p(\mathbf{x})=\underbrace{\mathbb{E} \log R}_{\text {bound }}+\underbrace{\mathbb{E} \log \frac{p(\mathbf{x})}{R}}_{\text {looseness }}\)
- (b) \(\log p(\mathbf{x})=\underbrace{\underset{q(\mathbf{z})}{\mathbb{E}} \log \frac{p(\mathbf{z}, \mathbf{x})}{q(\mathbf{z})}}_{\operatorname{ELBO}[q(\mathbf{z}) \mid \mid p(\mathbf{z}, \mathbf{x})]}+\underbrace{\operatorname{KL}[q(\mathbf{z}) \mid \mid p(\mathbf{z} \mid \mathbf{x})]}_{\text {divergence }}\).
-
why (b) than (a)?
- **increased flexibility **( alternative estimators \(R\) can give tighter bounds)
-
draw multiple i.i.d samples from \(q\) and average the estimates
\(R_{M}=\frac{1}{M} \sum_{m=1}^{M} \frac{p\left(\mathbf{z}_{m}, \mathbf{x}\right)}{q\left(\mathbf{z}_{m}\right)}, \mathbf{z}_{m} \sim q\).
Tighter bound, “importance weighted ELBO (IW-ELBO)”
\(\mathrm{IW}-\mathrm{ELBO}_{M}[q(\mathbf{z}) \mid \mid p(\mathbf{z}, \mathbf{x})]:=\underset{q\left(\mathbf{z}_{1: M}\right)}{\mathbb{E}} \log \frac{1}{M} \sum_{m=1}^{M} \frac{p\left(\mathbf{z}_{m}, \mathbf{x}\right)}{q\left(\mathbf{z}_{m}\right)}\).
- where \(\mathbf{z}_{1: M}\) is a shorthand for \(\left(\mathbf{z}_{1}, \ldots, \mathbf{z}_{M}\right)\)
- \(q\left(\mathbf{z}_{1: M}\right)=q\left(\mathbf{z}_{1}\right) \cdots q\left(\mathbf{z}_{M}\right)\).
3-1. A generative process for the importance weighted ELBO

IWVI (Importance Weighted Variational Inference)
- maximizing IW-ELBO
Generative Process for \(q_M\) ( \(\approx\) self-normalized importance sampling )
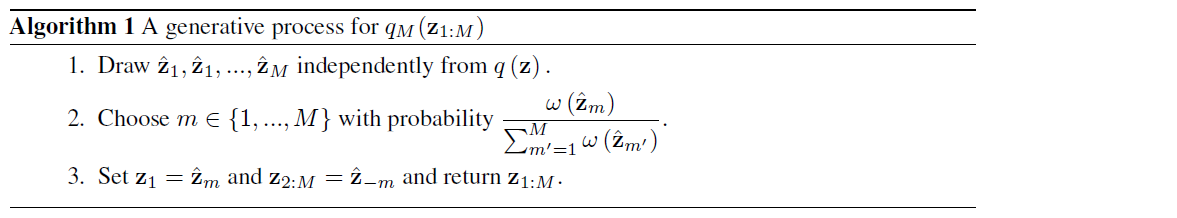
Previous works proved that….
\(\log p(\mathbf{x}) \geq \operatorname{ELBO}\left[q_{M}\left(\mathbf{z}_{1}\right) \mid \mid p\left(\mathbf{z}_{1}, \mathbf{x}\right)\right] \geq \mathbf{I W}-\mathrm{ELBO}_{M}[q(\mathbf{z}) \mid \mid p(\mathbf{z}, \mathbf{x})]\).
- IW-ELBO lower bounds ELBO
- KL-divergence is minimized by maximizing IW-ELBO
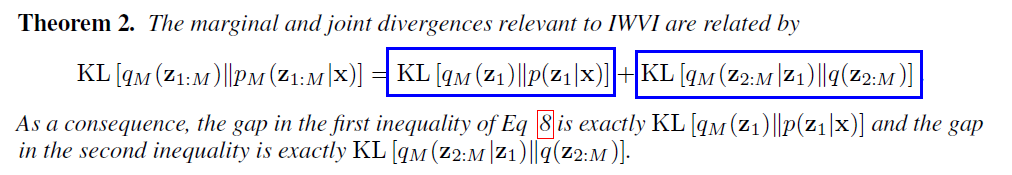
4. Importance Sampling Variance
consider family for the variational distribution
- small M : mode-seeking \(\rightarrow\) favor “weak tails”
- large M : variance reduction \(\rightarrow\) favor “wider tails”
5. After
나중에
