IntroVAE : Introspective Variational Autoencoders for Photographic Image Synthesis (NeurIPS 2018)

Abstract
introduce IntroVAE for synthesizing high-resolution photographic images
IntroVAE
- Introspective VAE
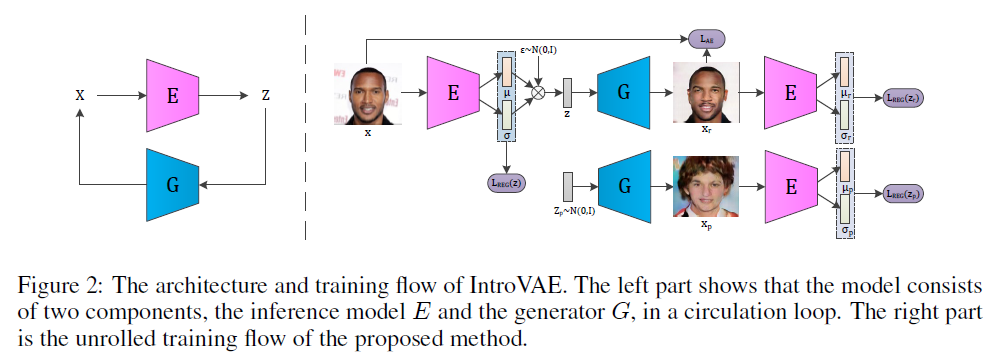
- inference & generator are JOINTLY trained
- generator : required to reconstruct input ( from the noisy output of inference model )
- inference model : encourage to classify REAL vs GENERATED
1. Introduction
generative models example
-
VAEs, GANs, RealNVP, GMMNs ( Generative moment matching networks )
-
2 most prominent models : VAEs & GANs
VAE & GAN
-
(GAN) require multi-scale discriminators to decompose “high” \(\rightarrow\) “from-low-to-high” resolution tasks
- (GAN/VAE) imposes discriminator on data space to improve the quality of the result generated
- also “hybrid models” exists…. still lage behind GANs in image quality
Introduce IntroVAE
- simple, yet effective approach to training VAEs!
- model can self-estimate the differences between REAL vs GENERATED
- (1) Inference model
- MINIMIZE divergence of “approximate posterior” & “prior for REAL data”
- MAXIMIZE divergence of “approximate posterior” & “prior for FAKE data”
-
(2) Generator model
- mislead the inference model
- MINIMIZE the divergence of generated samples
-
acts like VAE for real data
acts like GAN for generated data
Contribution :
-
1) new training technique for VAEs, in introspective manner
( model itself estimates the difference between REAL vs FAKE )
-
2) propose a single-stage adversarial model
2. Background
VAEs
- \(\log p_{\theta}(x) \geq E_{q_{\phi}(z \mid x)} \log p_{\theta}(x \mid z)-D_{K L}\left(q_{\phi}(z \mid x) \mid \mid p(z)\right)\).
- limitation : generated samples are BLURRY
GANs
-
min-max game
( 2 models : \(G\) ( generator ) & \(D\) ( discriminator ) )
-
\(\min _{G} \max _{D} E_{x \sim p_{\text {data }}(x)}[\log D(x)]+E_{z \sim p_{z}(z)}[\log (1-D(G(z)))]\).
-
promising tools for generating sharp images, but difficult to train
Hybrid Models of VAEs and GANs
usually consists of 3 components
- encoder
- decoder
- discriminator
[Ulyanov et al] adversarial generator-encoder networks (AGE)
- share similarities with IntroVAE
[Brock et al] Introspective Adversarial Network (IAN)
- encoder & discriminator share most of the layers except last layer
- adversarial loss is a “variation of the standard GAN loss”
3. Approach
how to train VAEs in introspective manner?
-
1) needs to discriminate REAL vs FAKE
-
2) should mislead 1)
Overview
-
Select inference model (=encoder) as “discriminator of GANs”
-
Select generator model as “generator of GANs”
-
Train Jointly!
2 components in ELBO of VAEs
- \(L_{A E}=-E_{q_{\phi}(z \mid x)} \log p_{\theta}(x \mid z)\).
- \(L_{R E G}=D_{K L}\left(q_{\phi}(z \mid x) \mid \mid p(z)\right)\).
\(\rightarrow\) modified combination of these 2 terms
3-1. Adversarial Distribution Matching
(1) Inference model
-
minimize \(L_{R E G}\)
( encourage posterior of REAL data to match prior )
-
maximize \(L_{R E G}\)
( encourage posterior of FAKE data to deviate from prior)
(2) Generator
- produce FAKE that have small \(L_{R E G}\)
2 different losses :
- to train inference model \(E\) : \(L_{E}(x, z)=E(x)+[m-E(G(z))]^{+}\)
- to train generator \(G\) : \(L_{G}(z)=E(G(z))\)
where \(E(x)=D_{K L}\left(q_{\phi}(z \mid x) \mid \mid p(z)\right)\) & \([\cdot]^{+}=\max (0, \cdot)\)
Relationships with other GANs
- proposed method appears to be similar to Energy-based GANs (EBGAN)
- proposed KL-divergence can be seen as a specific type of energy function
3-2. Introspective Variational Inference
(1) Prior : \(N(0, I)\)
(2) Posterior : \(q_{\phi}(z \mid x)=N\left(z ; \mu, \sigma^{2}\right)\)
- input \(z\) of \(G\) is sampled from posterior, using reparam trick
(3) KL-divergence ( \(L_{R E G}\) )
- \(L_{R E G}(z ; \mu, \sigma)=\frac{1}{2} \sum_{i=1}^{N} \sum_{j=1}^{M_{z}}\left(1+\log \left(\sigma_{i j}^{2}\right)-\mu_{i j}^{2}-\sigma_{i j}^{2}\right)\).
(4) Reconstruction error ( \(L_{A E}\) )…. MSE
- \[L_{A E}\left(x, x_{r}\right)=\frac{1}{2} \sum_{i=1}^{N} \sum_{j=1}^{M_{x}} \mid \mid x_{r, i j}-x_{i j}\mid \mid_{F}^{2}\]
Like VAE/GAN..
- train to discriminate samples from both the (1) model samples & (2) reconstructions
combined use of samples from \(p(z)\) and \(q_{\phi}(z \mid x)\) is expected to provide a more useful signal for the model to learn more expressive latent code and synthesize more realistic samples
Total Loss :
\(\begin{aligned} L_{E} &=L_{R E G}(z)+\alpha \sum_{s=r, p}\left[m-L_{R E G}\left(z_{s}\right)\right]^{+}+\beta L_{A E}\left(x, x_{r}\right) \\ &=L_{R E G}(\operatorname{Enc}(x))+\alpha \sum_{s=r, p}\left[m-L_{R E G}\left(\operatorname{Enc}\left(n g\left(x_{s}\right)\right)\right)\right]^{+}+\beta L_{A E}\left(x, x_{r}\right) \end{aligned}\).