Self-Supervised Representation Learning by Rotation Feature Decoupling
Contents
- Abstract
- Rotation feature decoupling
- Image rotation prediction
- Noisy rotated images
- Feature decoupling
0. Abstract
incorporates rotation invariance into feature learning
learns a split representation
- (1) rotation related part
- (2) rotation unrelated parts
jointly optimize NNs, by..
- (1) Rotation discrimination : predicting image rotations
- (2) Instance discrimination : discriminating individual instances
1. Rotation feature decoupling
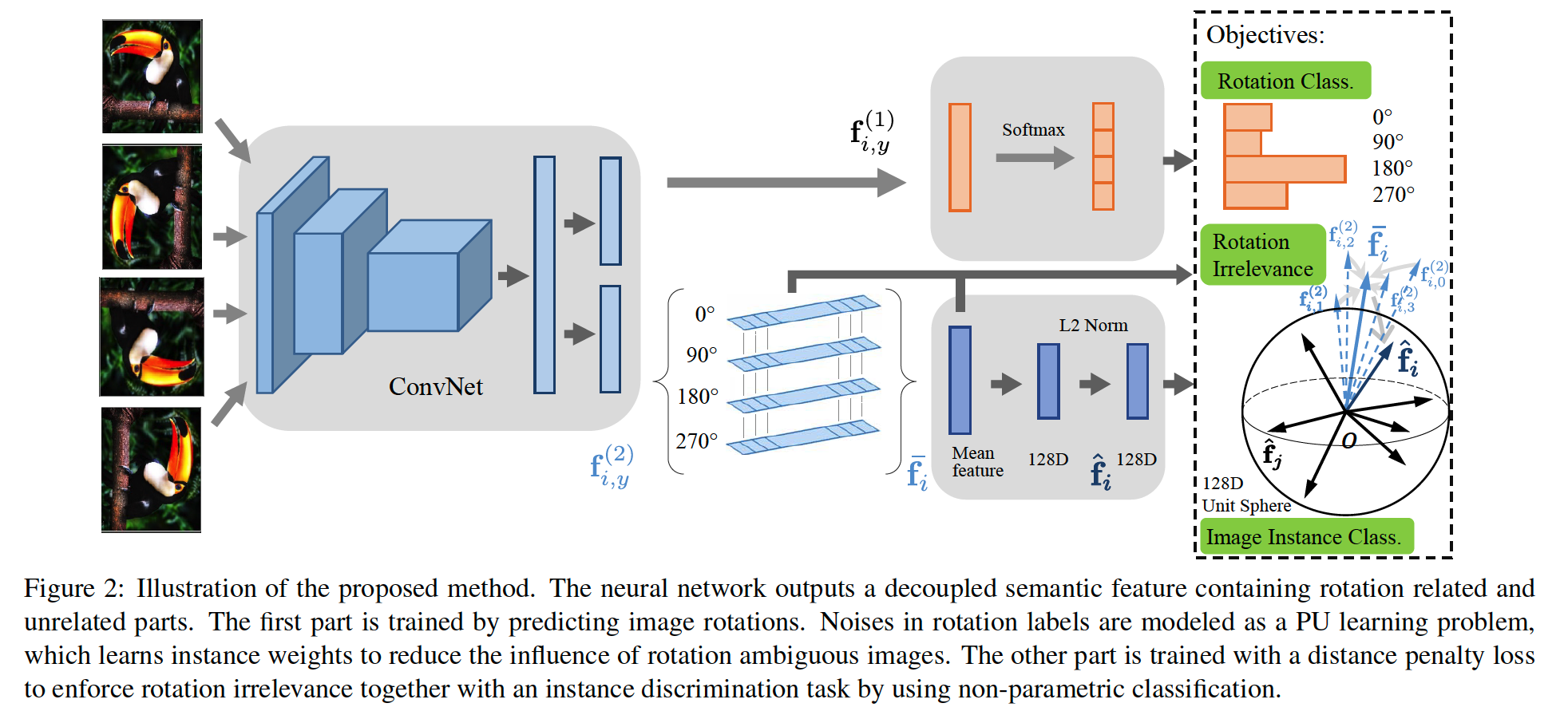
(1) Image rotation prediction
Notation
- \(S=\left\{X_{i}\right\}_{i=1}^{N}\) : training dataset
- \(\{g(X ; y)\}_{y=1}^{K}\) : set of rotational transformation
- \(X_{i, y}\) : \(i\)-th image with the \(y\)-th rotation
- where \(X_{i, y}=g\left(X_{i} ; y\right)\)
- \(F(\cdot ; \boldsymbol{\theta})\) : ConvNet model
- trained to classify each rotated image to one of the transformations
Objective : \(\min _{\boldsymbol{\theta}} \frac{1}{N K} \sum_{i=1}^{N} \sum_{y=1}^{K} l\left(F\left(X_{i, y} ; \boldsymbol{\theta}\right), y\right)\)
- \(l\) : cross-entropy
- ex) \(K=4\) : multiplies of 90 degrees
(2) Noisy rotated images
( basic premise of RotNet : rotating an image will change the orientation of objects in the images )
2 types of images
- orientation non-agnostic
- orientation agnostic
- not favored by ConvNets \(\rightarrow\) use weight!

apply PU learning framework
- positive = original images ( in default orientation )
- negative = rotated copies
solution : propose to weight each rotated image, using estimated probability
& reduce the relative loss of rotation ambiguous images
-
\(\tilde{F}\left(X_{i, y}\right)\) : probability of an image being positive estimated
-
\(w_{i, y}= \begin{cases}1 & y=1 \\ 1-\tilde{F}\left(X_{i, y}\right)^{\gamma} & \text { otherwise }\end{cases}\).
\(\rightarrow\) \(\min _{\boldsymbol{\theta}} \frac{1}{N K} \sum_{i=1}^{N} \sum_{y=1}^{K} w_{i, y} l\left(F\left(X_{i, y} ; \boldsymbol{\theta}\right), y\right)\)
Summary : predicts the image rotations, while mitigating the influence of noisy images
(3) Feature decoupling
rotation info…. Useful?
\(\rightarrow\) depends on the dataset!
[ Task 1 ] Rotation classification
\(\mathbf{f}=\left[\mathbf{f}^{(1)^{\top}}, \mathbf{f}^{(2)^{\top}}\right]^{\top}\).
- \(\mathbf{f}^{(1)}\) : related to image rotation
- \(\mathbf{f}^{(2)}\) : unrelated ~
( for image representation, concatenate \(\mathbf{f}^{(1)}\) and \(\mathbf{f}^{(2)}\) )
Rotation classification loss :
- fixed size vector : \(\mathbf{f}_{i, y}=F_{f}\left(X_{i, y} ; \boldsymbol{\theta}_{f}\right) .\)
- loss : \(\mathcal{L}_{c}=\frac{1}{N K} \sum_{i=1}^{N} \sum_{y=1}^{K} w_{i, y} l\left(F_{c}\left(\mathbf{f}_{i, y}^{(1)} ; \boldsymbol{\theta}_{c}\right), y\right)\)
[ Task 2 ] Rotation irrelevance
Given rotated copies of images \(\left\{X_{y}\right\}_{y=1}^{K}\),
their features \(\left\{\mathbf{f}_{y}^{(2)}\right\}_{y=1}^{K}\) are expected to be similar
\(\rightarrow\) Minimize between \(\left\{\mathbf{f}_{y}^{(2)}\right\}_{y=1}^{K}\) and \(\overline{\mathbf{f}}=\frac{1}{K} \sum_{y=1}^{K} \mathbf{f}_{y}^{(2)}\)
Rotation irrelevance loss :
- \(\mathcal{L}_{r}=\frac{1}{N K} \sum_{i=1}^{N} \sum_{y=1}^{K} d\left(\mathbf{f}_{i, y}^{(2)}, \overline{\mathbf{f}}_{i}\right)\).
- \(d\) : Euclidean distance
Problem : but…. can simply output same vector (e.g. zero vector)
\(\rightarrow\) solution : “Image instance classification”
[ Task 3 ] Image instance classification
probability of predicting \(X\) as the \(i\)-th instance : \(P(i \mid \hat{\mathbf{f}})=\frac{\exp \left(\hat{\mathbf{f}}_{i}^{\top} \hat{\mathbf{f}} / \tau\right)}{\sum_{j=1}^{N} \exp \left(\hat{\mathbf{f}}_{j}^{\top} \hat{\mathbf{f}} / \tau\right)}\).
Negative log-likelihood :
- \(\mathcal{L}_{n}=-\sum_{i=1}^{N} \log P\left(i \mid \hat{\mathbf{f}}_{i}\right)\).
[ Total Loss ]
\(\min _{\boldsymbol{\theta}_{f}, \boldsymbol{\theta}_{c}} \lambda_{c} \mathcal{L}_{c}+\lambda_{r} \mathcal{L}_{r}+\lambda_{n} \mathcal{L}_{n}\).
