Self-Supervised GANs via Auxiliary Rotation Loss
Contents
- Abstract
- A Key Issue : Discriminator Forgetting
- The Self-Supervised GAN
0. Abstract
Conditional GAN : necessity for labeled data
This paper : exploit 2 techniques
- (1) adversarial training (GAN)
- (2) self-supervision
\(\rightarrow\) bridge the gap between conditional & unconditional GANs
collaborate on task of representation learning,
being adversarial w.r.t classical GAN
1. A Key Issue : Discriminator Forgetting
Original GAN loss :
\(\begin{aligned} V(G, D)=& \mathbb{E}_{\boldsymbol{x} \sim P_{\mathrm{data}}(\boldsymbol{x})}\left[\log P_{D}(S=1 \mid \boldsymbol{x})\right] \\ &+\mathbb{E}_{\boldsymbol{x} \sim P_{G}(\boldsymbol{x})}\left[\log \left(1-P_{D}(S=0 \mid \boldsymbol{x})\right)\right] \end{aligned}\).
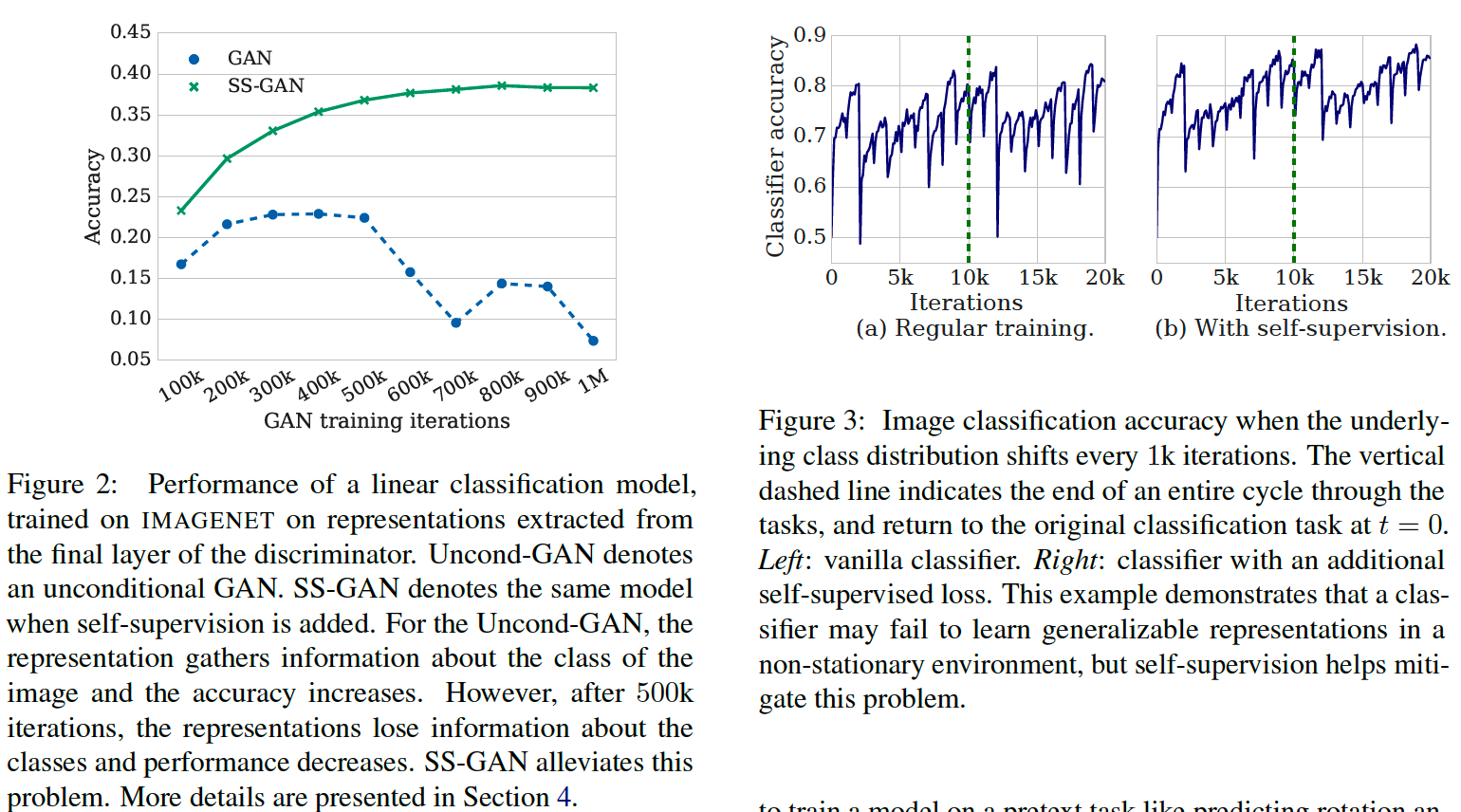
- in online learning of non-convex functions, NN have been shown to forget previous tasks!
Impact of discriminator forgetting in 2 settings
-
(1) Figure 3 (a)
-
( 1 vs all classifier ) x 10 times
-
no useful information is carreid across tasks
\(\rightarrow\) the model does not retain generalizable representations in this non-stationary environment
-
-
(2) Figure 2
2. The Self-Supervised GAN
aim to imbue the discriminator with mechanism, which allows learning useful representations
\(\rightarrow\) use self-supervised approach
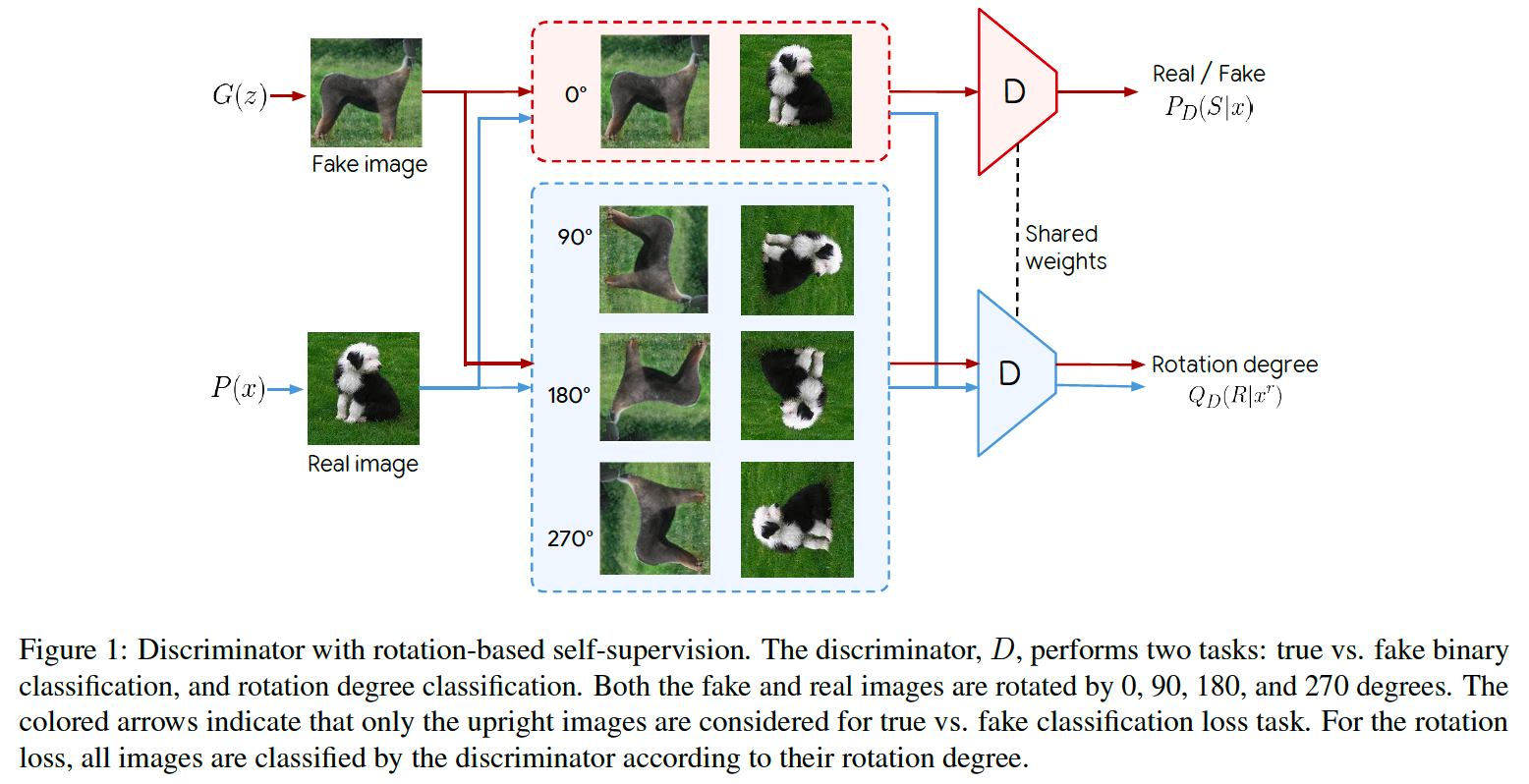
Image Rotation task
- propose to add a self-supervised task to discriminator
- improvement : shown in Figure 3 (b)
- \(D\) & \(G\) “collaborate” w.r.t rotation task
Loss Function ( with rotation-based loss )
\(\begin{aligned} &L_{G}=-V(G, D)-\alpha \mathbb{E}_{\boldsymbol{x} \sim P_{G}} \mathbb{E}_{r \sim \mathcal{R}}\left[\log Q_{D}\left(R=r \mid \boldsymbol{x}^{r}\right)\right] \\ &L_{D}=V(G, D)-\beta \mathbb{E}_{\boldsymbol{x} \sim P_{\text {data }}} \mathbb{E}_{r \sim \mathcal{R}}\left[\log Q_{D}\left(R=r \mid \boldsymbol{x}^{r}\right)\right] \end{aligned}\).
- \(\mathcal{R}=\left\{0^{\circ}, 90^{\circ}, 180^{\circ}, 270^{\circ}\right\}\).
Details : use a single \(D\) with 2 heads to compute \(P_D\) & \(Q_D\)
