(paper 47) DINO

Emerging Properties in Self-Supervised Vision Transformers

Contents

1. Abstract
2. Introduction
3. Approach
   1. SSL with Knowledge Distillation
   2. Implementation & Evaluation Protocols

0. Abstract

Make the following observations

• (1) self-supervised ViT features contain explicit information about the semantic segmentation of an image
• (2) these features are also excellent k-NN classifiers

Underlines the importance of …

• (1) momentum encoder
• (2) multi-crop training
• (3) use of small patches with ViTs

Implement these findings into a simple self-supervised method, DINO

• form of self-distillation with no labels

1. Introduction

DINO :

• simplifies self-supervised training, by directly predicting the output of a teacher network, using CE loss

• teacher network = built with a momentum encoder

• work with only a centering and sharpening of the teacher output to avoid collapse

• flexible and works on both convnets and ViTs

  ( without the need to modify the architecture )

2. Approach

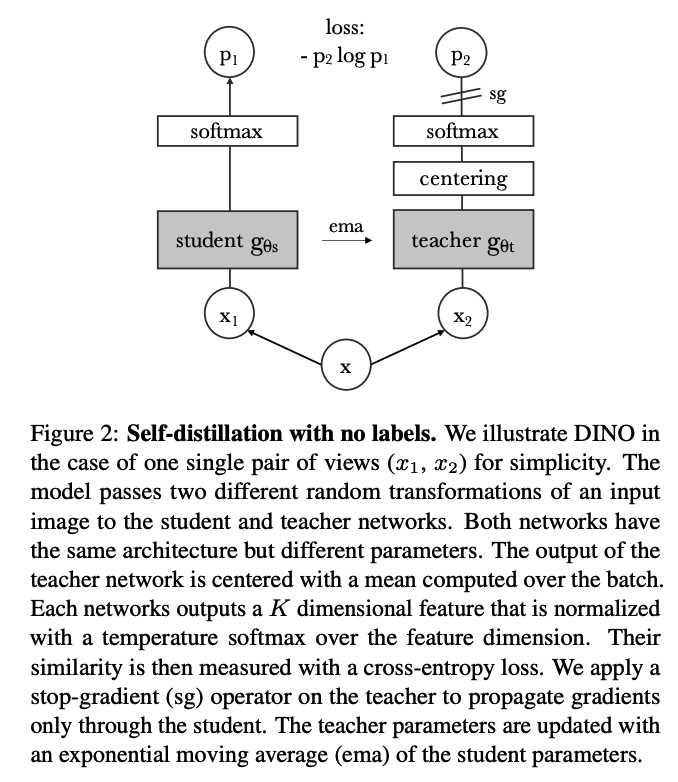
(1) SSL with Knowledge Distillation

shares the overall structure of…

• (1) SSL
• (2) Knowledge distillation

a) Knowledge distillation

• train a student network \(g_{\theta_s}\), to match the output of a given teacher network \(g_{\theta_t}\)
  • student & teacher : same network structure / different parameter
• given input \(x\), both networks output probability distributions
  • over K dimensions denoted by \(P_s\) & \(P_t\)
  • \(P_s(x)^{(i)}=\frac{\exp \left(g_{\theta_s}(x)^{(i)} / \tau_s\right)}{\sum_{k=1}^K \exp \left(g_{\theta_s}(x)^{(k)} / \tau_s\right)}\).

Given a fixed teacher network \(g_{\theta_t}\) …

\(\rightarrow\) learn to match these distributions by minimizing the CE w.r.t \(\theta_s\)

( = \(\min _{\theta_s} H\left(P_t(x), P_s(x)\right)\) .)

Details : How to construct different distorted views?

\(\rightarrow\) with multicrop strategy

b) Multicrop strategy

• generate a set \(V\) of different views.
  • 2 global views ( \(x_1^g\) and \(x_2^g\) )
  • \(V-2\) local views ( of smaller resolution )

Input of…

• student NN : All crops
• teacher NN : global views

\(\rightarrow\) encouraging “local-to-global” correspondences

Loss function : \(\min _{\theta_s} \sum_{x \in\left\{x_1^g, x_2^g\right\}} \sum_{\substack{x^{\prime} \in V \\ x^{\prime} \neq x}} H\left(P_t(x), P_s\left(x^{\prime}\right)\right)\).

\(\rightarrow\) learn \(\theta_s\) by minimizing the above!

c) Teacher Network

build it from past iterations of the student network (EMA)

• \(\theta_t \leftarrow \lambda \theta_t+(1-\lambda) \theta_s\).

d) Network architecture \(g\)

\(g=h \circ f\) … composed of

• (1) backbone \(f\) ( = ViT, ResNet… )
• (2) projection head \(h\)
  • 2-1) 3-layer MLP with dim=2048
  • 2-2) followed by \(\ell_2\) norm
  • 2-3) weight normalized FC layer with \(K\) dim

e) Avoiding Collapse

SSL methods : differ by the operation ….

• used to avoid collapse
• contrastive loss
• clustering constraints
• predictor
• batch normalizations…

Proposed Methods :

work with only a centering and sharpening of the momentum teacher outputs to avoid model collapse

(1) centering :

• prevents one dimension to dominate, but encourages collapse to the uniform distribution,

(2) sharpening :

• opposite effect

\(\rightarrow\) Applying both : balances their effects … thus avoid collapse

Center \(c\) : updated with EMA

• \(c \leftarrow m c+(1-m) \frac{1}{B} \sum_{i=1}^B g_{\theta_t}\left(x_i\right)\).

(2) Implementation & Evaluation Protocols