SVM & KKT
Contents
- Introduction of SVM
- Notation
- Geometry
- SVM Margin maximization
- Dual of SVM Margin maximization
- Complementary Slackness Condition (CSC)
- KKT condition
- KKT for quadratic minimization
- Water filling algorithm
1. Introduction of SVM
(1) Notation
Feature vectors :
- \(\mathbf{x}_{\mathbf{i}} \in \mathbf{R}^{\mathbf{p}}, \mathbf{i}=\mathbf{1}, \ldots, \mathbf{n}\).
Labels :
- \(\mathbf{y}_{\mathbf{i}} \in\{-\mathbf{1}, \mathbf{1}\}, \mathbf{i}=\mathbf{1}, \ldots, \mathbf{n}\).
(2) Geometry
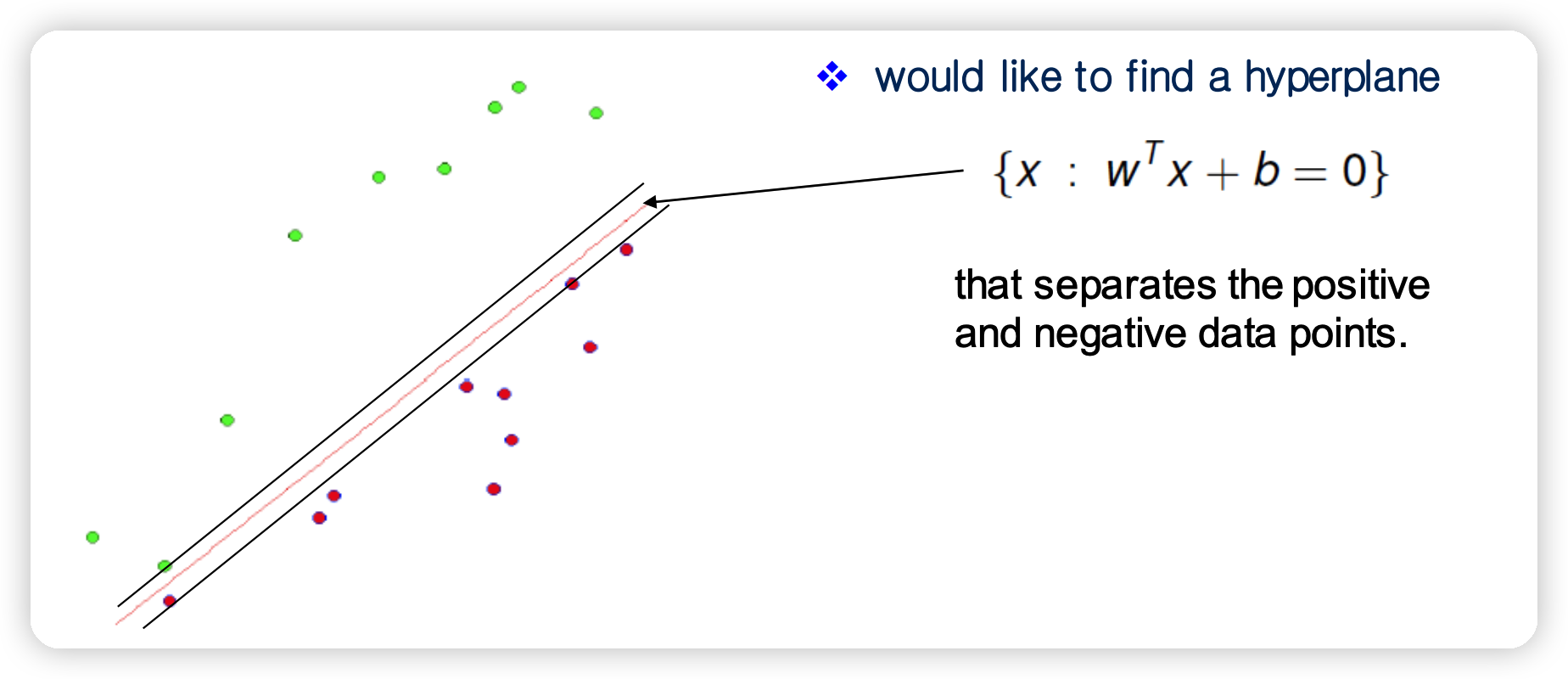
Strictly 구분 가능 (separable)하다고 가정 했을 때, 아래의 조건이 충족하도록 \(w\)와 \(b\)를 scale할 수 있다.
- \(y_i(w^T x_i + b) \geq 1\) , where \(i = 1, \cdots n\)
Margin = 2 hyperplane 사이의 거리
- \(2 / \mid \mid w \mid \mid_2\).
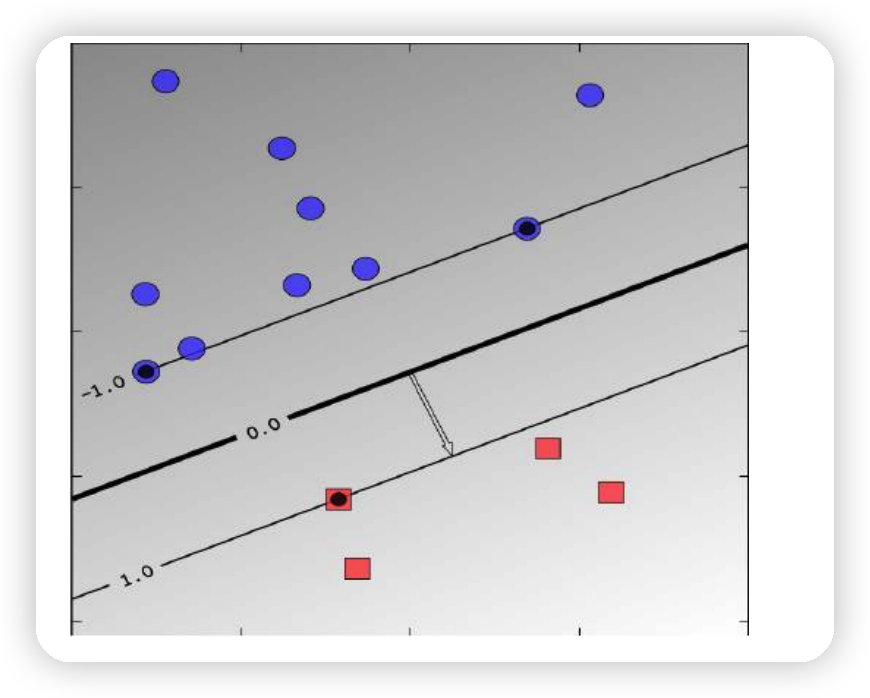
2. SVM Margin maximization
Original Goal :
\(\begin{aligned} &\text { maximize } \frac{2}{ \mid \mid \mathrm{w} \mid \mid _{2}} \\ &\text { s.t. } \quad \mathrm{y}_{\mathrm{i}}\left(\mathrm{w}^{\mathrm{T}} \mathrm{x}_{\mathrm{i}}+\mathrm{b}\right) \geq 1, \forall \mathrm{i} \end{aligned}\).
이는 곧 아래와 동일하다.
\(\begin{array}{ll} \operatorname{minimize} \frac{1}{2} \mid \mid \mathrm{w} \mid \mid_{2}^{2} \\ \text { s.t. } \mathrm{y}_{\mathrm{i}}\left(\mathrm{w}^{\mathrm{T}} \mathrm{x}_{\mathrm{i}}+\mathrm{b}\right) \geq 1, \forall \mathrm{i} \end{array}\).
# 3. Dual of SVM Margin maximization
\(\underset{\alpha}{\operatorname{maximize}} \sum_{i=1}^{n} \alpha_{i}-\frac{1}{2} \sum_{i=1}^{n} \sum_{j=1}^{n} \alpha_{i} \alpha_{j} y_{i} y_{j}\left(X_{i}^{T} \cdot X_{j}\right)\).
such that
- \(\sum_{i=1}^{n} \alpha_{i} y_{i}=0\).
- \(\alpha_{i} \geq 0 \quad \forall \mathrm{i}\).
4. Complementary Slackness Condition (CSC)
Strong duality가 충족된다고 가정해보자.
( 즉, \(f_{0}\left(x^{\star}\right)=g\left(\lambda^{\star}, \nu^{\star}\right)\) )
Notation
- \(p^{*}\) : primal optimal
- \((\lambda^{*},v^*)\) : dual optimal
\(\begin{aligned} f_{0}\left(x^{\star}\right)=g\left(\lambda^{\star}, \nu^{\star}\right) &=\inf _{x}\left(f_{0}(x)+\sum_{i=1}^{m} \lambda_{i}^{\star} f_{i}(x)+\sum_{i=1}^{p} \nu_{i}^{\star} h_{i}(x)\right) \\ & \leq f_{0}\left(x^{\star}\right)+\sum_{i=1}^{m} \lambda_{i}^{\star} f_{i}\left(x^{\star}\right)+\sum_{i=1}^{p} \nu_{i}^{\star} h_{i}\left(x^{\star}\right) \\ & \leq f_{0}\left(x^{\star}\right) \end{aligned}\).
- \(x^{\star}\) 는 \(L(x, \lambda^{\star}, v^{\star})\) 를 minmize한다
Complementary Slackness :
- \(\lambda_i^{\star} f_i(x^{\star})=0\) for \(i = 1 \cdots m\)
5. KKT condition
(1) 4가지 조건
- Primal Feasibility : primal problem의 제약조건들을 만족함
- \(f_{i}(x) \leq 0, i=1, \ldots, m\).
- \(h_{i}(x)=0, i=1, \ldots, p\).
- Dual Feasibility : dual problem의 제약조건들을 만족함
- \(\lambda \succeq 0\).
- Complementary Slackness :
- \(\lambda_{i} f_{i}(x)=0, i=1, \ldots, m\) ( 둘 중 하나는 0 )
- Gradient of Lagrangian w.r.t \(x\) vanishes ( stationarity )
- \(\nabla f_{0}(x)+\sum_{i=1}^{m} \lambda_{i} \nabla f_{i}(x)+\sum_{i=1}^{p} \nu_{i} \nabla h_{i}(x)=0\).
만약 STRONG duality가 hold + \(x, \lambda, v\) 아 optimal이면
\(\rightarrow\) 이들은 KKT condition을 충족한다.
( KKT condition은 optimality를 만족하기 위한 필요 조건 이다 )
만약, \(x, \lambda, v\)가 convex problem에 대해 KKT를 만족하면,
\(\rightarrow\) optimal이다!
( KKT condition은 optimality를 만족하기 위한 충분 조건 이기도 하다! )
6. KKT for quadratic minimization
\(\begin{array}{ll}\text { minimize } & (1 / 2) x^{T} P x+q^{T} x+r \\ \text { subject to } & A x=b,\end{array}\).
KKT condition
- (1) Primal Feasibility: \(A x^{*}=b\)
- (2) Dual Feasibility \& C.S.C: N/A
- (3) Gradient: \(P x^{\star}+q+A^{T} \nu^{\star}=0\)
이를 정리하면…
\(\left[\begin{array}{cc} P & A^{T} \\ A & 0 \end{array}\right]\left[\begin{array}{l} x^{\star} \\ \nu^{\star} \end{array}\right]=\left[\begin{array}{c} -q \\ b \end{array}\right]\).
- \(m+n\) 개의 variable
- \(m+n\) 개의 constraints
Example
Minimize \(f(x, y)=x^{2}+y^{2}+x y\)
subject to \(x+3 y=5\)
\(P=\left[\begin{array}{ll} 2 & 1 \\ 1 & 2 \end{array}\right] \quad A=\left[\begin{array}{ll} 1 & 3 \end{array}\right]\).
\(\left[\begin{array}{cc} P & A^{T} \\ A & 0 \end{array}\right]\left[\begin{array}{l} x^{\star} \\ \nu^{\star} \end{array}\right]=\left[\begin{array}{c} -q \\ b \end{array}\right]\) \(\rightarrow\) \(\left[\begin{array}{lll} 2 & 1 & 1 \\ 1 & 2 & 3 \\ 1 & 3 & 0 \end{array}\right]\left[\begin{array}{c} x \\ y \\ v \end{array}\right]=\left[\begin{array}{l} 0 \\ 0 \\ 5 \end{array}\right]\).
\(\rightarrow\) \(F\left(x^{*}, y^{*}\right)=3.1065\).
7. Water filling algorithm
\(\begin{array}{ll} \operatorname{minimize} & -\sum_{i=1}^{n} \log \left(\alpha_{i}+x_{i}\right) \\ \text { subject to } & x \succeq 0, \quad 1^{T} x=1 \end{array}\).
