[Implicit DGM] 13. Wasserstein GAN

[Implicit DGM] 13. Wasserstein GAN

( 참고 : KAIST 문일철 교수님 : 한국어 기계학습 강좌 심화 3)

Contents

1. Difference of Two Probability Distributions
2. Integral Probability Metric (IPM)
   1. Total Variation Distance
   2. Wasserstein metric
   3. Maximum Mean Discrepancy (MMD)
3. GAN + MMD

1. Why Wasserstein GAN?

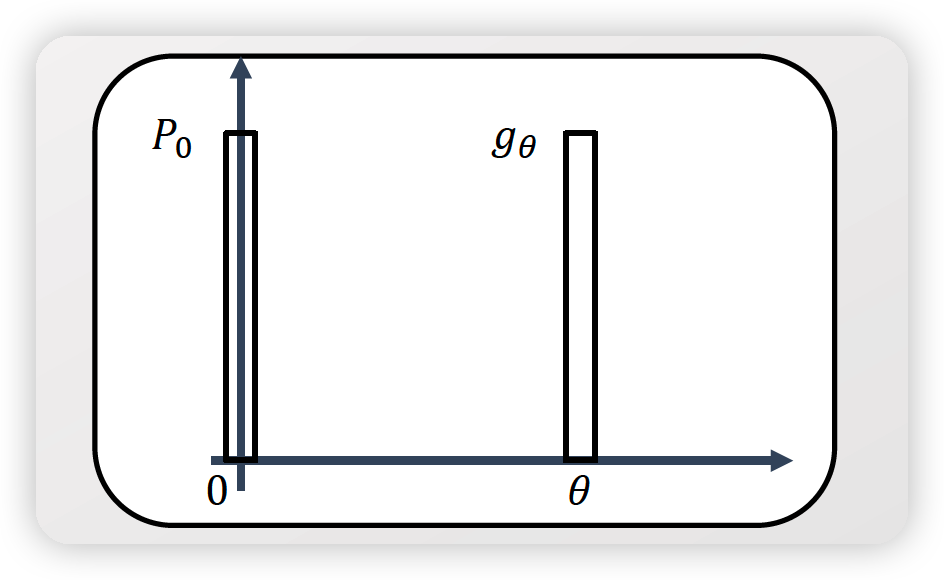
Example) Parallel Line Density

• \(Z \sim U[0,1]\).
• 2 distributions
  • \(P_{0}:\) distn of \((0, Z) \in R^{2}\)
  • \(g_{\theta}(z)=(\theta, z), \theta \in R\),
    • \(\theta\) : parameter of Generator function

\(\rightarrow\) (Conclusion) Wasserstein metric is the only metric as a continuous function

(1) Total Variation distance

\(\mathcal{G}\) : class of all measurable functions, with value in \([0,1]\)

• \(\delta\left(P_{r}, P_{g}\right)=\sup _{A \in \Sigma} \mid P_{r}(\mathrm{~A})-\mathrm{P}_{\mathrm{g}}(\mathrm{A}) \mid\).
• \(\delta\left(P_{0}, P_{g}\right)=\left\{\begin{array}{l} 1, \text { if } \theta \neq 0 \\ 0, \text { if } \theta=0 \end{array}\right.\).

(2) Wasserstein metric

\(\mathcal{G}\) : class of 1-Lipschitz functions

• \(W\left(P_{r}, P_{g}\right)=\inf _{\gamma \in \Pi\left(P_{r}, P_{\mathrm{g}}\right)} \mathrm{E}_{(\mathrm{x}, \mathrm{y}) \sim \gamma}[ \mid \mid \mathrm{x}-\mathrm{y} \ \mid ]\).
• \(W\left(P_{0}, P_{g}\right)= \mid \theta \mid\).

(3) KL divergence

• \(D_{K L}\left(P_{r} \ \mid P_{g}\right)=\int P_{r}(x) \log \frac{P_{r}(x)}{P_{g}(x)} d x\).
• \(D_{K L}\left(P_{0} \ \mid P_{g}\right)=D_{K L}\left(P_{g} \ \mid P_{0}\right)=\left\{\begin{array}{c}\infty, \text { if } \theta \neq 0 \\ 0, \text { if } \theta=0\end{array}\right.\).

(4) JS divergence

• \(D_{J S}\left(P_{r} \mid \mid P_{g}\right)=\frac{1}{2} D_{K L}\left(P_{r} \mid \mid \frac{P_{r}+P_{g}}{2}\right)+\frac{1}{2} D_{K L}\left(P_{g} \mid \mid \frac{P_{r}+P_{g}}{2}\right)\).
• \(D_{J S}\left(P_{r} \ \mid P_{g}\right)= \begin{cases}\log 2 & \text {, if } \theta \neq 0 \\ 0 & , \text { if } \theta=0\end{cases}\).

\(\rightarrow\) (2) 빼고는 전부 \(\theta\) 에 대해 gradient가 smooth하지 않다!

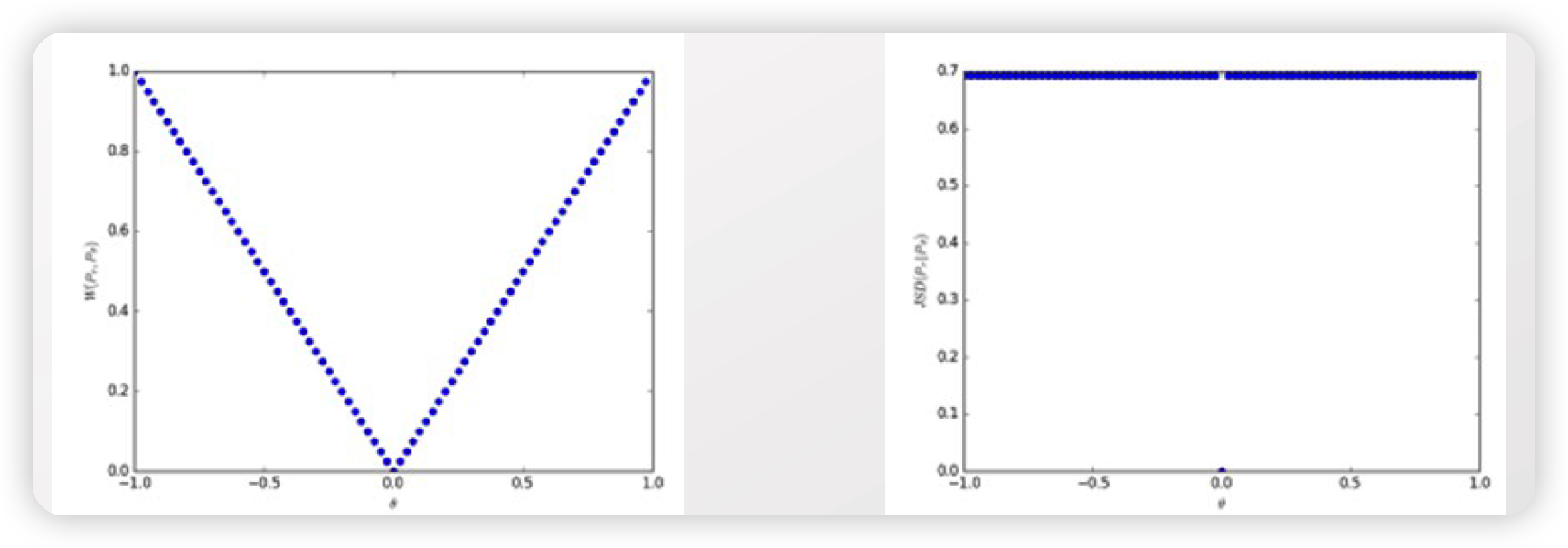
• (left) Wassersetin metric
• (right) JS divergence

2. Wasserstein Distance with GAN

(1) WGAN

Original Wasserstein distance

• \(W\left(P_{r}, P_{g}\right)=\inf _{\gamma \in \Pi\left(P_{r}, \mathrm{P}_{\mathrm{g}}\right)} \mathrm{E}_{(\mathrm{x}, \mathrm{y}) \sim \gamma}[ \mid \mid \mathrm{x}-\mathrm{y} \mid \mid ]\).

GAN objective

• \(\min _{G} \max _{D} E_{x \sim p_{\text {data }(x)}}[\log D(x)]+E_{z \sim p_{z}(z)}[\log (1-D(G(z))]\).

How to put \(W\left(P_{r}, P_{g}\right)\) inside the objective function?

• (GAN) in marginal distn ( \(P_{r}\) and \(P_{\mathrm{g}}\) )
  • acceptable complexity, since \(P_r\) & \(P_g\) can be calculated by sampling multiple times
• (WGAN) in joint distn ( \(\Pi\left(P_{r}, P_{\mathrm{g}}\right)\) )
  • complexity : \(O(X \times X)\).

(2) Kantorovich-Rubin Duality

LP problem

• (Primal) Minimize \(\mathrm{c}^{T} \mathrm{x}\), subject to \(Ax=b, x\geq 0\)
• (Dual) Maximize \(b^{T} \mathrm{y}\), subject to \(A^{T} \mathrm{y} \leq \mathrm{c}\)

Optimization

• choosing an instance of \(\gamma\) from \(\Pi\left(P_{r}, P_{\mathrm{g}}\right)\), to minimize \(W\left(P_{r}, P_{g}\right)\)

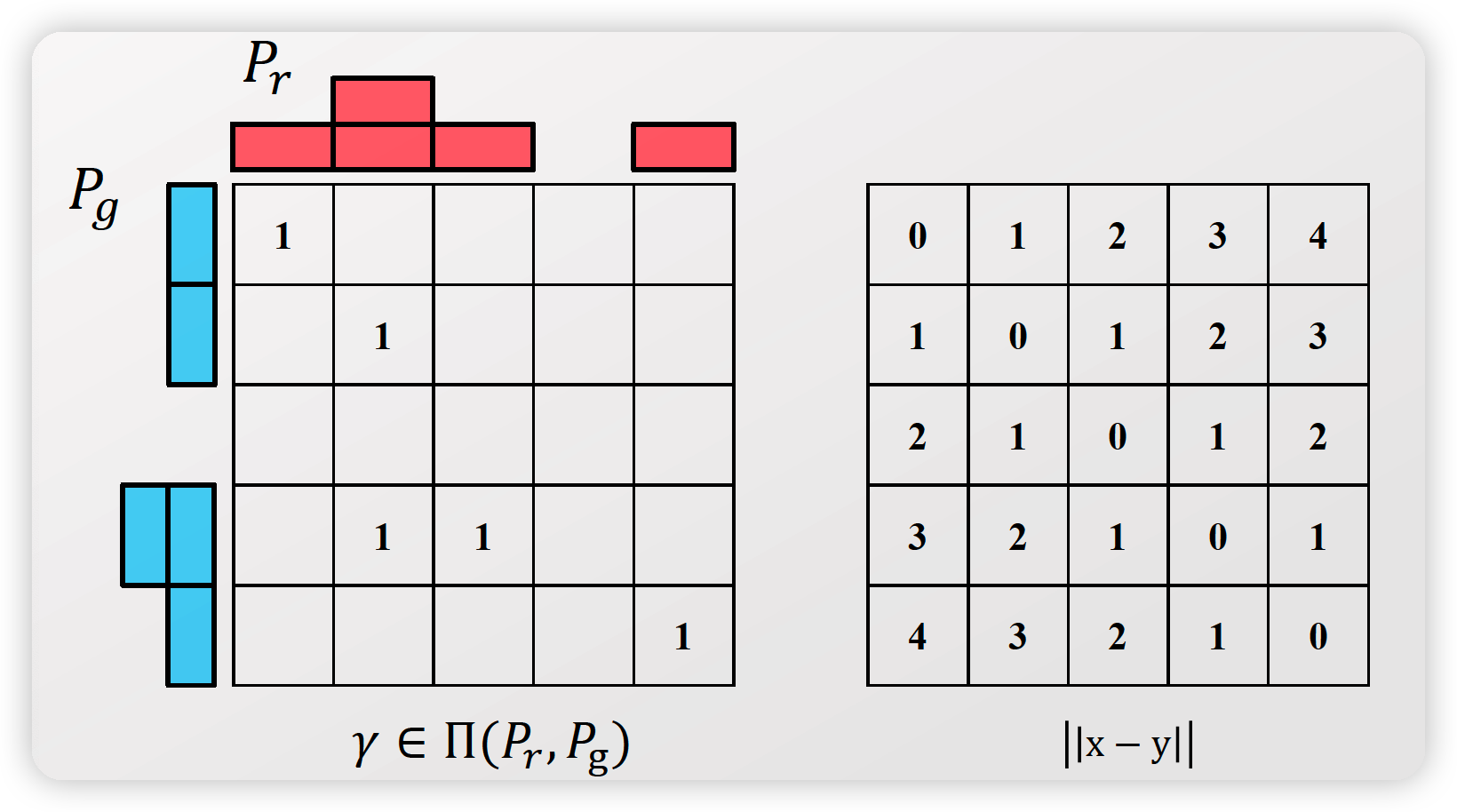
Should be close to DIAGONAL !!

( far from diagonal = more movement = more cost )

(3) Wasserstein as Primal / Dual LP

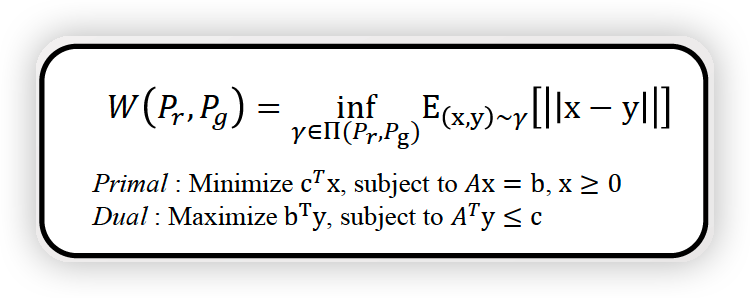
(Primal) Minimize \(\mathrm{c}^{T} \mathrm{x}\), subject to \(Ax=b, x\geq 0\)

• \(Ax=b\) : hard constraint
  • marginal distribution 합 유지하기
• \(x\) : decision variable ( = optimization variable )
  • \(\gamma\)의 각 cell 값
• \(c^T\) : objective function
  • earth movement의 distance

Primal

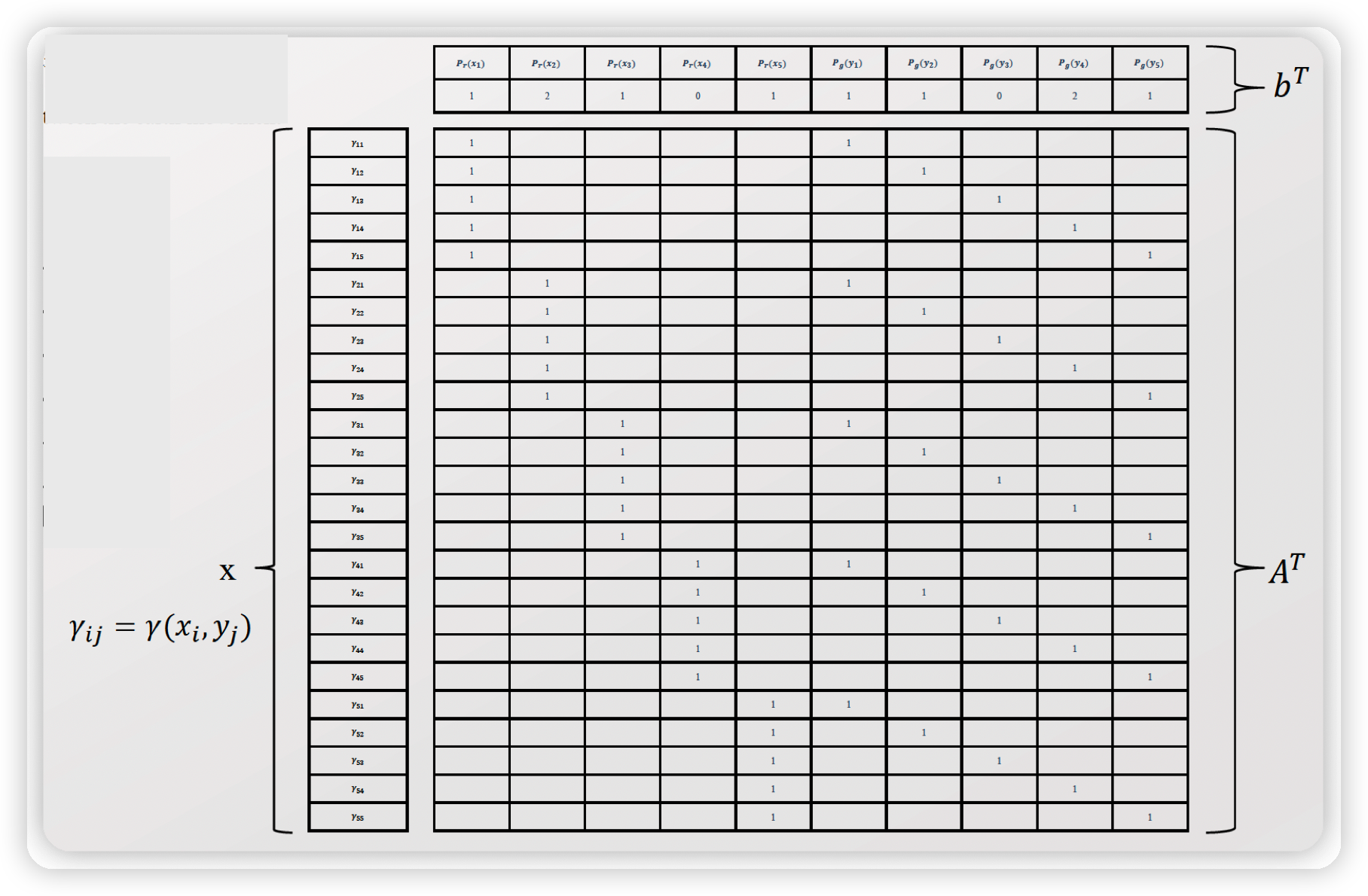
해석

• \(x\) : \(\gamma_{ij}(x_i,y_j)\) 로써, 5x5 = 25개
• \(b^T\) : \(P_r(x_i)\) , \(P_g(x_i)\) 로써, 5x2 = 10개
• \(A^T\) : 25x10 matrix

\(\rightarrow\) deicision variable은 \(x\) 다

Dual

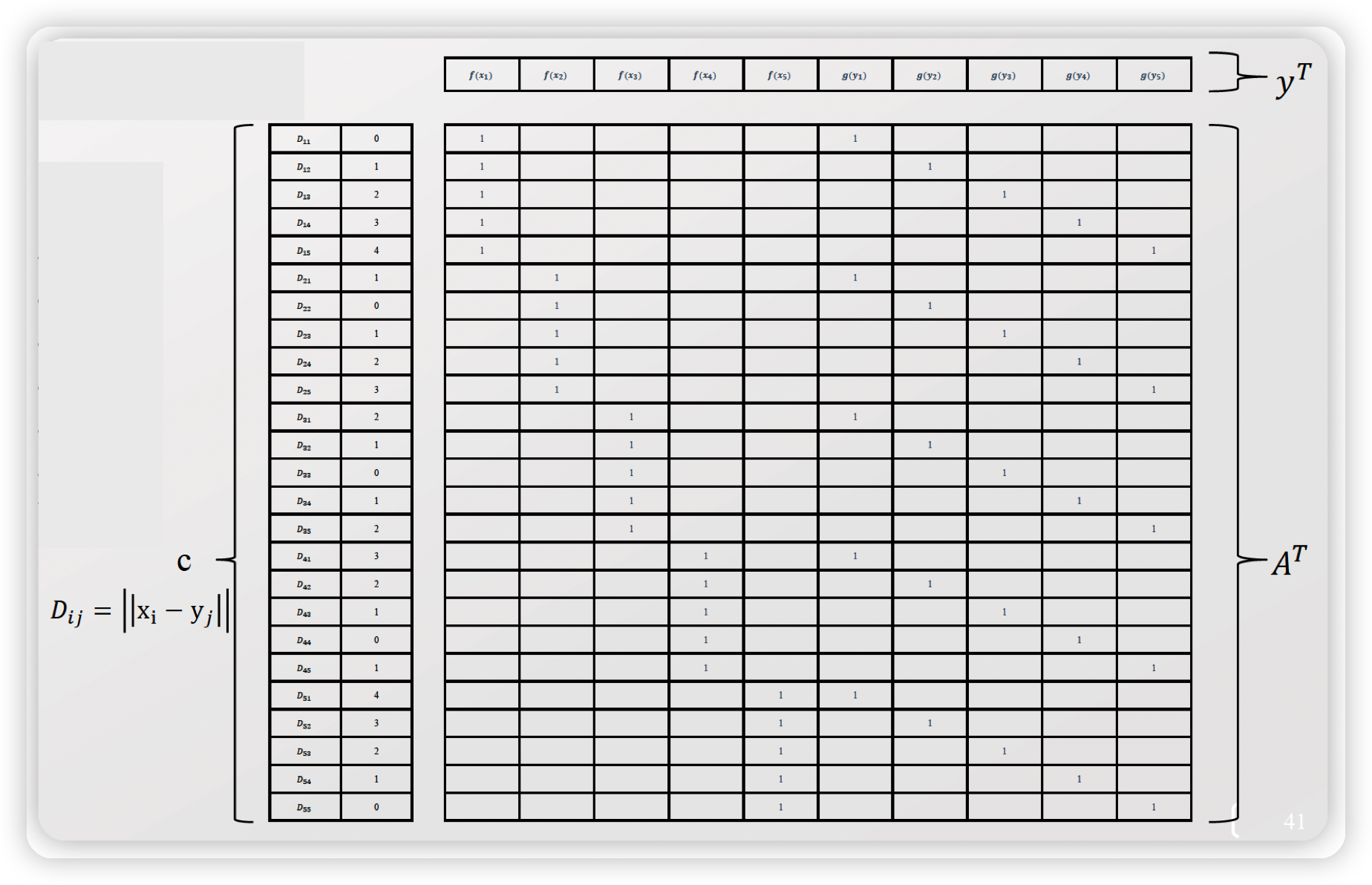
해석

• \(c\) : \(D_{ij} = \mid \mid x_i - y_j \mid \mid\) 로써, 5x5 = 25개
• \(y^T\) : \(f(x_i)\) , \(g(y_i)\) 로써, 5x2 = 10개
• \(A^T\) : 25x10 matrix

\(\rightarrow\) deicision variable은 \(y\) 다

(4) Property of Dual LP on Wasserstein Distance

Primal of Wasserstein Distance :

• \(W\left(P_{r}, P_{g}\right)=\inf _{\gamma \in \Pi\left(P_{r}, P_{\mathrm{g}}\right)} \mathrm{E}_{(\mathrm{x}, \mathrm{y}) \sim \gamma}[ \mid \mid \mathrm{x}-\mathrm{y} \mid \mid ]\).

Dual constraints :

( 제약조건 : \(A^{T} \mathrm{y} \leq \mathrm{c}\) )

• 모든 \(i,j\) 에 대해, \(f\left(x_{i}\right)+g\left(y_{j}\right) \leq D_{i, j}\).

  • If \(i=j, f\left(x_{i}\right)+g\left(y_{i}\right) \leq D_{i, i}=0\)

• diagonal일 때 optimal

  • \(f\left(x_{i}\right)+g\left(y_{i}\right)=0 \rightarrow f\left(x_{i}\right)=-g\left(y_{i}\right)\).

  • \(f\left(x_{i}\right)+g\left(y_{j}\right) \leq D_{i, j} \rightarrow f\left(x_{i}\right)-f\left(x_{j}\right) \leq D_{i, j}\).

• 이러한 제약조건은, \(f\)의 variation을 제약함

  ( = Lipschitz constraint of \(f\) )

즉, 만약 \(f\)가 Lipschitz constraint하다는 제약조건만 걸면, constraint \(A^{T} \mathrm{y} \leq \mathrm{c}\) 에 대해서는 더 이상 고려하지 않아도 된다.

3. Lipschitz Continuity

\(f\left(x_{i}\right)+g\left(y_{j}\right) \leq D_{i, j} \rightarrow f\left(x_{i}\right)-f\left(x_{j}\right) \leq D_{i, j}\),

Lipschitz Continuity :

• 2개의 metric space \((X,d_x)\) & \((Y,d_y)\)가 주어졌을 때,
• function \(f: X \rightarrow Y\) 는 다음의 경우 Lipschitz continuous하다
  • \(d_{Y}\left(f\left(x_{1}\right), f\left(x_{2}\right)\right) \leq K d_{X}\left(x_{1}, x_{2}\right)\) 를 만족하는 \(K\) ( = Lipschitz constant )가 존재한다.
• Ex) absolute difference :
  • \(\mid f\left(x_{1}\right)-f\left(x_{2}\right) \mid \leq K \mid x_{1}-x_{2} \mid\).

그렇다면, NN은 Lipschitz continuous한가?

\(\rightarrow\) NP-hard…

4. Dual Problem of Wasserstein Distance

Notation

• \(f, \gamma\) : decision variable
• \(A\) : matrix between
  • \(\gamma_{i,j}\) & \(b\) ( primal )
  • \(D_{i,j}\) & \(y\) ( dual )
• \(D_{i,j}\) : earth movement 거리
• \(b\) : marginal distn ( \(P_r\) & \(P_g\) 를 concantenate )

(1) Primal

Minimize \(\mathrm{c}^{T} \mathrm{x}\), subject to \(A \mathrm{x}=\mathrm{b}, \mathrm{x} \geq 0\)

Primal of Wasserstein Distance :

• \(W\left(P_{r}, P_{g}\right)=\inf _{\gamma \in \Pi\left(P_{r}, P_{g}\right)} \mathrm{E}_{(\mathrm{x}, \mathrm{y}) \sim \gamma}[ \mid \mid \mathrm{x}-\mathrm{y} \mid \mid ]\).

(2) Dual

Maximize \(\mathrm{b}^{\mathrm{T}} \mathrm{y}\), subject to \(A^{T} \mathrm{y} \leq \mathrm{c}\)

Dual of Wasserstein Distance :

• \(W\left(P_{r}, P_{g}\right)=\max _{f} E_{P_{r}}[f(x)]+E_{y \sim P_{g}}[g(y)]\).

  • constraint : \(f\left(x_{i}\right)+g\left(y_{j}\right) \leq D_{i, j}\)

  • constraint : \(f\left(x_{i}\right)+g\left(y_{i}\right)=0 \rightarrow f\left(x_{i}\right)=-g\left(y_{i}\right), f\left(x_{i}\right)-f\left(y_{j}\right) \leq D_{i, j}\)

    ( = \(f\) to be Lipschitz continuous )

5. Kantorovich-Rubinstein Duality & Wasserstein GAN

Kantorovich-Rubinstein Theorem

• \(W\left(p_{r}, p_{g}\right)=\inf _{\gamma \in \Pi(p, q)} E_{(x, y) \sim \gamma}[ \mid x-y \mid ]=\sup _{ \mid \mid f \ \mid _{L} \leq 1}\left[E_{x \sim p_{r}}[f(x)]-E_{y \sim p_{g}}[f(x)]\right]\).

기존 GAN

• \(\min _{G} \max _{D} E_{x \sim p_{\text {data }(x)}}[\log D(x)]+E_{z \sim p_{z}(z)}[\log (1-D(G(z))]\).

WGAN

• (max) 두 분포 사이의 Wasserstein metric 계산 위해
  • \(W\left(P_{r}, P_{g}\right)=\max _{f} E_{P_{r}}[f(x)]-E_{y \sim P_{g}}[f(y)]\).
• (min) 두 분포 사이의 거리가 가깝도록 하기 위해
  • \(\min _{P_{g}} W\left(P_{r}, P_{g}\right)=\min _{P_{g}} \max _{f} E_{P_{r}}[f(x)]-E_{y \sim P_{g}}[f(y)]\).

• Wasserstein metric 만들기 위한 constraint :

  \(\rightarrow\) Lipshitz constraint of \(f\)