(paper 85) M2m; Imbalanced Classification via Major-to-Minor Translation

M2m: Imbalanced Classification via Major-to-Minor Translation

Contents

1. Abstract
2. Introduction
3. M2m: Major-to-minor translation
   1. Overview of M2m
   2. Underlying intuition on M2m
   3. Detailed components of M2m
4. Experiments
   1. Experimental Setup
   2. Long-tailed CIFAR datasets
   3. Real-world Imbalanced datasets
   4. Ablation Study
5. Conclusion

0. Abstract

Labeled training datasets : highly class-imbalanced

Explore a NOVEL yet SIMPLE way to alleviate this issue :

\(\rightarrow\) Augmenting less-frequent classes* via TRANSLATING samples from more-frequent classes*

\(\rightarrow\) enables a classifier to learn more generalizable features of minority classes,

• by transferring and leveraging the diversity of the majority information.

Improves the generalization on minority classes significantly

• compared to other existing (1) re-sampling or (2) re-weighting methods

1. Introduction

Datasets in research : CI- FAR [25] and ILSVRC [39]

\(\leftrightarrow\) Real-world datasets : suffer from its expensive data acquisition process and the labeling cost.

\(\rightarrow\) leads a dataset to have a “LONG TAILED” label distribution

Solution: Two categories

Rebalance the training objective w.r.t class-wise sample size!!

• (a) Re-weighting
  • re-weight the the loss function
  • by a factor inversely proportional to the sample frequency in a class-wise manner
• (b) Re-sampling
  • re-sample the given dataset
    • “over-sampling” the minority classes
    • “under- sampling” the majority classes

However, re-balancing the objective usually results in harsh “overfitting to minority classes”, since they cannot handle the lack of minority information in essence.

To solve this issue…

• Cui et al. [7] : proposed “effective number”
  • number of samples as alternative weights in the re-weighting method.
• Cao et al. [4] : both re-weighting and re-sampling can be much more effective when applied at the later stage of training in NN
• SMOTE [5] : widely-used variant of the over-sampling method
  • that mitigates the overfitting via data augmentation
  • several variants of SMOTE have been suggested accordingly
  • major drawback : perform poorly when there exist only a few samples in the minority classes, ( = “extreme” imbalance )
    • because they synthesize a new minority sample only using the existing samples of the same class.

Other works:

(1) Regularization scheme

• minority classes are more penalized
• margin-based approaches generally suit well as a form of data-dependent regularizer

(2) Vew the class-imbalance problem in the framework of Active learning or Meta-learning

Contribution

• revisit the over-sampling framework
• propose Major-to-minor Translation (M2m).
  • a new way of generating minority samples

M2m

1. M2m vs. SMOTE

• SMOTE :
  • applies **data augmentation to minority samples **to mitigate the over-fitting issue
• M2m :
  • does not use the existing minority samples for the oversampling.
  • use the majority samples and translate them to the target minority class
    • using another classifier independently trained ( under the imbalanced dataset )

1. Effective on learning more generalizable features in imbalanced learning:

• does not overly use the minority samples
• leverages the richer information of the majority samples

1. Architecture : consists of 3 components
   1. Optimization objective for generating synthetic samples:
      • a majority sample can be translated into a synthetic minority sample via optimizing it, while not affecting the performance of the majority class
   2. Sample rejection criterion
      • generation from “more” majority class is more preferable.
   3. Optimal distribution
      • which majority seed to translate??

Evaluation

Evaluate our method on various imbalanced classification problems

• (1) Synthetically imbalanced datasets
  • from CIFAR-10/100 and ImageNet
• (2) Real-world imbalanced datasets
  • CelebA, SUN397, Twitter and Reuters

Summary

• Significantly improves the balanced test accuracy compared to previous re-sampling or re-weighting methods across all the tested datasets.

• Surpass LDAM ( current SOTA margin-based method. )

• Particularly effective under “extreme” imbalance

2. M2m: Major-to-minor translation

Settings

• cls with \(K\) classes
• dataset : \(\mathcal{D}=\left\{\left(x_i, y_i\right)\right\}_{i=1}^N\),
  • where \(x \in \mathbb{R}^d\) and \(y \in \{1, \cdots, K\}\)
• \(f: \mathbb{R}^d \rightarrow \mathbb{R}^K\) : a classifier designed to output \(K\) logits,
• \(N:=\sum_k N_k\) : the total sample size of \(\mathcal{D}\),
  • \(N_k\) : sample size of class \(k\).
  • assume \(N_1 \geq N_2 \geq \cdots \geq N_K\).

Class-conditional data distn \(\mathcal{P}_k:=p(x \mid y=k)\)

• are assumed to be invariant across training and test time
• have different prior distributions, say \(p_{\text {train }}(y)\) and \(p_{\text {test }}(y)\),
  • \(p_{\text {train }}(y)\) : highly imbalanced
  • \(p_{\text {test }}(y)\) : assumed to be the uniform distn

Primary goal of the class-imbalanced learning :

• train \(f\) from \(\mathcal{D} \sim \mathcal{P}_{\text {train }}\) that generalizes well under \(\mathcal{P}_{\text {test }}\)
• loss function \(\mathcal{L}(f)\) : \(\min _f \mathbb{E}_{(x, y) \sim \mathcal{D}}[\mathcal{L}(f ; x, y)]\)

M2m : over-sampling technique

• assume a “virtually balanced” training dataset \(\mathcal{D}_{\text {bal }}\) made from \(\mathcal{D}\) such that the class \(k\) has \(N_1-N_k\) more samples,
• \(f\) is trained on \(\mathcal{D}_{\text {bal }}\) ( instead of \(\mathcal{D}\) )

Key challenge in over-sampling : prevent overfitting on minority classes

• In contrast to most prior works that focus on performing data augmentation directly on minority samples….

  \(\rightarrow\) M2m augment minority samples in a completely different way!

  • does not use the minority samples for the augmentation, but the majority samples.

(1) Overview of M2m

Train \(f\) on a class-imbalanced \(\mathcal{D}\).

Major-to-minor Translation (M2m)

• construct a new balanced dataset \(\mathcal{D}_{\text {bal }}\) for training \(f\),

  • by adding synthetic minority samples that are translated from other samples of (relatively) majority classes.

• Multiple ways to perform this “Major-to-minor” translation.

  • Cross-domain generation via GAN

    • much computational cost for additional training

  • M2m

    • much simpler and efficient approach:

      \(\rightarrow\) translate a majority sample by optimizing it to maximize the target minority confidence of another baseline classifier \(g\).

Classifier \(g\) & \(f\)

• \(g\) : classifier pre-trained NN on \(\mathcal{D}\)

  ( so that performs well on the training IMBALANCED dataset )

  • thus \(g\) may be over-fitted to minority classes

• \(f\) : the target network aim to train to perform well on the BALANCED testing criterion.

  • while training \(f\) , M2m utilizes the \(g\) to generate new minority samples
  • generated samples are added to \(\mathcal{D}\) to construct \(\mathcal{D}_{\text {bal }}\) on the fly.

Translates a majority seed \(x_0\) into \(x^*\)

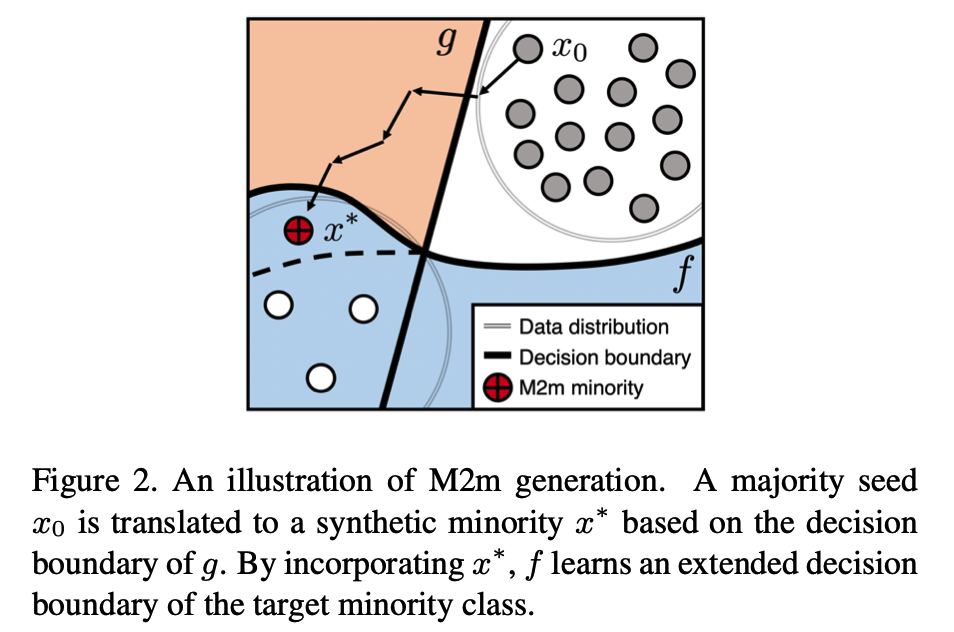
( from class \(k_0\) to \(k\) )

To obtain a single synthetic minority \(x^*\) of class \(k\), solve an optimization problem as below!

Starting from another training sample \(x_0\) of a (relatively) major class \(k_0<k\) :

\(x^*=\underset{x:=x_0+\delta}{\arg \min } \mathcal{L}(g ; x, k)+\lambda \cdot f_{k_0}(x)\)….. (2)

• \(\mathcal{L}\) : CE loss

Generated sample \(x^*\) :

• labeled to class \(k\)
• fed into \(f\) for training to perform better on \(\mathcal{D}_{\text {bal }}\)

Do not force \(f\) in (2) to classify \(x^*\) to class \(k\) as well,

but restrict \(f\) to have lower confidence on the original class \(k_0\)

• by imposing a regularization term \(\lambda \cdot f_{k_0}(x)\).

Regularization term \(\lambda \cdot f_{k_0}(x)\)

• reduces the risk when \(x^*\) is labeled to \(k\), whereas it may contain significant features of \(x_0\) in the viewpoint of \(f\).

\(\rightarrow\) Teach \(f\) to learn novel minority features which \(g\) considers it significant,

( via extension of the decision boundary from the knowledge \(g\). )

(2) Underlying intuition on M2m

\(g\) : “oracle” classifier

Solving \(x^*=\underset{x:=x_0+\delta}{\arg \min } \mathcal{L}(g ; x, k)+\lambda \cdot f_{k_0}(x)\)

= essentially requires a transition of \(x_0\) of class \(k_0\) with \(100 \%\) confidence to another class \(k\) with respect to \(g\)

Problem?

• this would let \(g\) “erase and add” the features related to the class \(k_0\) and \(k\), respectively.

\(\rightarrow\) M2m : collect more in-distribution minority data!

However, NNs are very far from this ideal behavior!

• often finds \(x^*\) that is very close to \(x_0\),

\(\rightarrow\) But M2m still effectively improves the generalization of minority classes even in such cases.

Hypothesize this counter-intuitive effectiveness of our method comes from mainly in two aspects:

• (a) Sample diversity in the majority dataset is utilized to prevent overfitting on the minority classes
• (b) Another classifier \(g\) is enough to capture the information in the small minority dataset.

\(\rightarrow\) Adversarial examples from a majority to a minority can be regarded as one of natural ways to leverage the diverse features in majority examples useful to improve the generalization of the minority classes.

Etc ) not replacing the existing dataset, but augmenting it!

(3) Detailed components of M2m

a) Sample Rejection Criterion

Impotant factor : Quality of \(g\) ( especially for \(g_{k_0}\))

• Good \(g_{k_0}\) = effectively “erase” important features of \(x_0\) during the translation

  \(\rightarrow\) making the resulting minority samples more reliable.

However, \(g\) is not that perfect in reality!

• Synthetic samples still contain some discriminative features of the original class \(k_0\) ( may harm the performance of \(f\) )
• This risk of “unreliable” generation becomes more harsh when \(N_{k_0}\) is small, as we assume that \(g\) is also trained on the given imbalanced dataset \(\mathcal{D}\).

Solution : a simple criterion for rejecting each of the synthetic samples randomly with probability depending on \(k_0\) and \(k\)

• \(\mathbb{P}\left(\text { Reject } x^* \mid k_0, k\right):=\beta^{\left(N_{k_0}-N_k\right)^{+}},\).
  • where \((\cdot)^{+}:=\max (\cdot, 0)\), and \(\beta \in[0,1)\) is a hyperparameter which controls the reliability of \(g\)

Hyperparameter \(\beta\)

• the smaller \(\beta\), the more reliable \(g\)

• ex) if \(\beta=0.999 (0.9999)\),
  • the synthetic samples are accepted with probability more than \(99 \%\) if \(N_{k_0}-N_k>4602 (46049)\).
• Motivated by the effective number of samples
  • impact of adding a single data point exponentially decreases at larger datasets.

When a synthetic sample is rejected….

• replace it by an existing minority sample from the original dataset \(\mathcal{D}\)

b) Optimal Seed Sampling

How to choose a (majority) seed sample \(x_0\) with class \(k_0\) ??

Based on the proposed rejection criterion proposed…

Design a sampling distribution \(Q\left(k_0 \mid k\right)\) for selecting the class \(k_0\) of initial point \(x_0\) given target class \(k\)

Consider 2 aspects

• (a) \(Q\) maximizes the acceptance probability \(P_{\text {accept }}\left(k_0 \mid k\right)\) under our rejection criterion

• (b) \(Q\) chooses diverse classes as much as possible

  ( = entropy \(H(Q)\) is maximized. )

Optimization : \(\max _Q[\underbrace{\mathbb{E}_Q\left[\log P_{\text {accept }}\right]}_{\text {(a) }}+\underbrace{H(Q)}_{\text {(b) }}] .\)

• \(Q=P_{\text {accept }}\) is the solution

Thus, we choose \(Q\left(k_0 \mid k\right) \propto 1-\beta^{\left(N_{k_0}-N_k\right)^{+}}\)

• once \(k_0\) is selected, a sample \(x_0\) is sampled uniformly!

c) Practical implementation via re-sampling.

M2m is implemented using a batch-wise re-sampling.

To simulate the generation of \(N_1-N_k\) samples for any \(k=2, \cdots, K\),

• generation with probability \(\frac{N_1-N_{y_i}}{N_1}=1-N_{y_i} / N_1\), for all \(i\) in a given class-balanced mini-batch \(\mathcal{B}=\left\{\left(x_i, y_i\right)\right\}_{i=1}^m\)

Step 1) For a single generation at index \(i\),

• sample \(k_0 \sim Q\left(k_0 \mid y_i\right)\) following \(Q\left(k_0 \mid k\right) \propto 1-\beta^{\left(N_{k_0}-N_k\right)^{+}}\) until \(k_0 \in\left\{y_i\right\}_{i=1}^m\)
• select a seed \(x_0\) of class \(k_0\) randomly inside \(\mathcal{B}\).

Step 2) Solve the \(x^*=\underset{x:=x_0+\delta}{\arg \min } \mathcal{L}(g ; x, k)+\lambda \cdot f_{k_0}(x)\)

• for a fixed number of iterations \(T\) with a step size \(\eta\).
• accept \(x^*\) only if \(\mathcal{L}\left(g ; x^*, y_i\right)\) is less than \(\gamma>0\) for stability.

Step 3) If accepted, we replace \(\left(x_i, y_i\right)\) in \(\mathcal{B}\) by \(\left(x^*, y_i\right)\).

3. Experiments

Various class-imbalanced classification tasks:

• synthetically-imbalanced variants of
  • CIFAR-10/100
  • ImageNet-LT
  • CelebA
  • SUN397
  • Twitter
  • Reuters

Metrics:

• (1) balanced accuracy (bACC)
  • essentially equivalent to the standard accuracy metric for balanced datasets.
• (2) geometric mean scores (GM)
  • defined by the arithmetic and geometric mean over class-wise sensitivity

Results: minority synthesis via translating from majority consistently improves the efficiency of over-sampling!

(1) Experimental Setup

a) Baseline methods.

• (a) empirical risk minimization (ERM)
  • training on the CE loss without any re-balancing
• (b) re-sampling (RS)
  • balancing the objective from different sampling probability for each sample
• (c) SMOTE
  • variant of re-sampling with data augmentation
• (d) re-weighting (RW)
  • balancing the objective from different weights on the sample-wise loss
• (e) class-balanced re-weighting (CB-RW)
  • variant of re-weighting that uses the inverse of effective number for each class, defined as \(\left(1-\beta^{N_k}\right) /(1-\beta)\).
    • Here, we use \(\beta=0.9999\)
• (f) deferred re-sampling (DRS)
• (g) deferred re-weighting (DRW)
  • re-sampling and reweighting is deferred until the later stage of the training, repsectively
• (h) focal loss
  • objective is upweighted for relatively hard examples to focus more on the minority
• (i) label-distribution-aware margin (LDAM)
  • trained to impose larger margin to minority classes.

\(\rightarrow\) These can be classified into three categories

• a) “re-sampling” based methods : (b), (c), (f)
• b) “re-weighting” based methods : (d), (e), (g)
• c) different loss functions : (a), (h), (i)

b) Training Details

Optimizer : SGD with momentum of weight 0.9.

• initial learning rate = 0.1

• and “step decay” is performed during training

• adopt the “linear warm-up” learning rate strategy in the first 5 epochs

(1) CIFAR-10/100 and CelebA

• we train ResNet-32 for 200 epochs
• batch size 128
• weight decay of \(2 \times 10^{-4}\).

(2) SUN397

• pre-activation ResNet-18

• All the input images are normalized over the training dataset,

  & and have the size of \(32 \times 32\) either by cropping or re-sizing

(3) Twitter and Reuter

• train 2-layer FC for 15 epochs
• batch size 64
• weight decay of \(5 \times 10^{-5}\).

c) Details on M2m.

Classifier \(g\)

• same architecture to \(f\)
• pretrained on the given (imbalanced) dataset ( via standard ERM training )

Deferred scheduling

• start to apply our method after the standard ERM training for a fixed number of epochs.

Hyperparameters

• fixed set of candidates
• \(\beta \in\{0.9,0.99,0.999\}, \lambda \in\{0.01,0.1,0.5\}\) and \(\gamma \in\{0.9,0.99\}\) based on the validation set.
• Unless otherwise stated, we fix \(T=10\) and \(\eta=0.1\) when performing a single generation step.

(2) Long-tailed CIFAR datasets

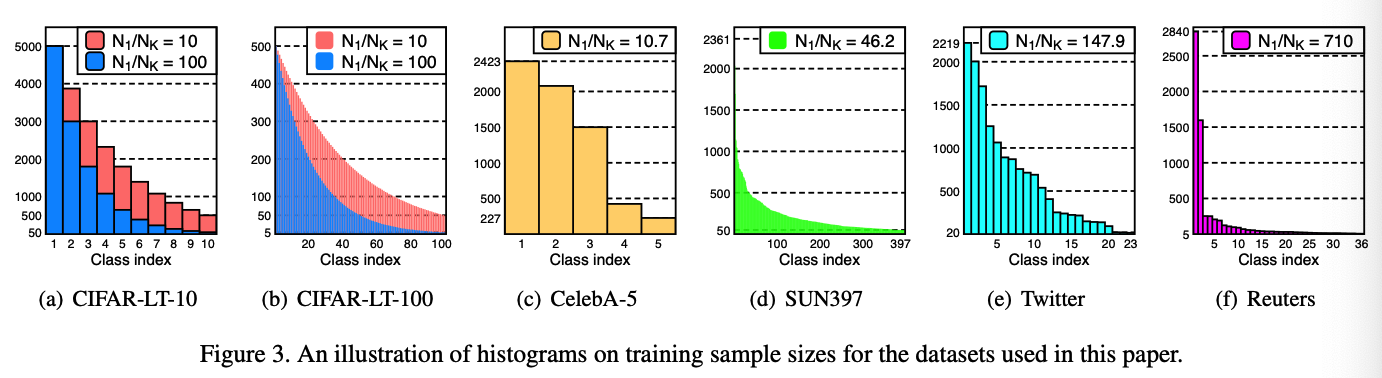
CIFAR-LT-10/100

• to evaluate our method on various levels of imbalance,

Control the imbalance ratio \(\rho>1\)

• artificially reduce the training sample sizes of each class except the first class, so that:
  • (a) \(N_1 / N_K\) equals to \(\rho\)
  • (b) \(N_k\) in between \(N_1\) and \(N_K\) follows an exponential decay across \(k\).

Keep the test dataset unchanged during this process ( = perfectly balanced ) - measuring accuracy on this test dataset = measuring the balanced accuracy
Two imbalance ratios $$\rho \in\{100,10\}$$ - each for CIFAR-LT-10 and 100.
### Results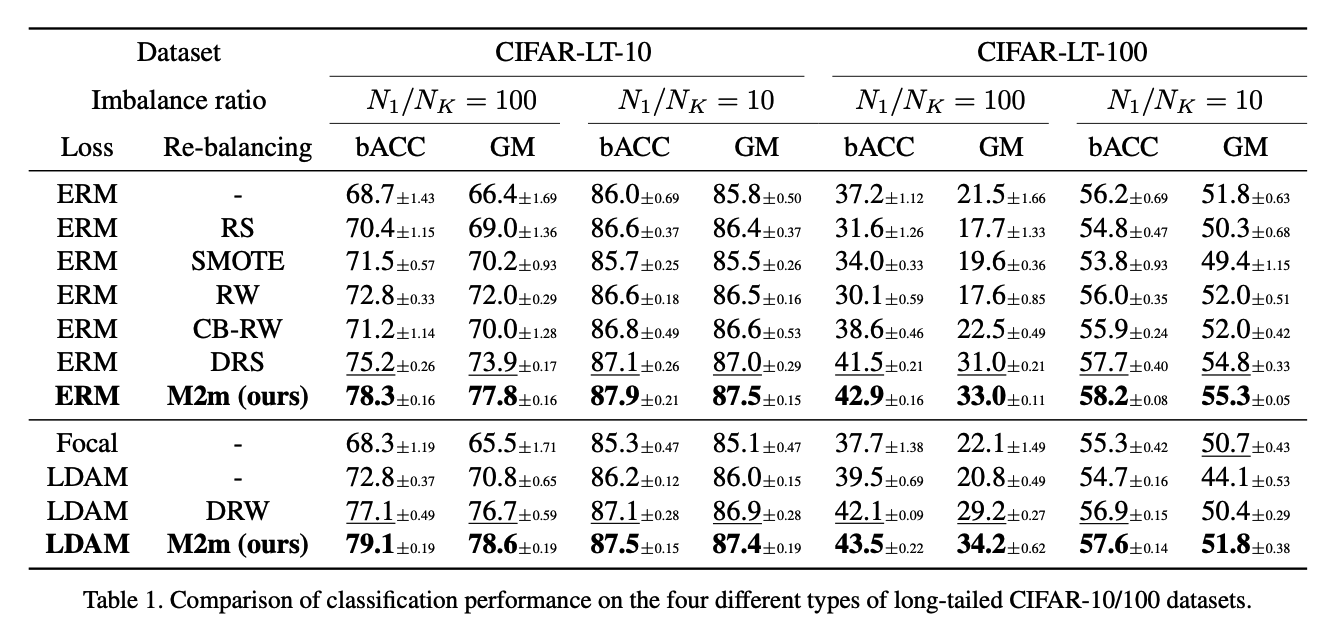 
## (3) Real-world Imbalanced datasets Datasets : CelebA, SUN397, Twitter and Reuters
CelebA : - originally a multi-labeled dataset - port this to a 5-way classification task ( by filtering only the samples with five non-overlapping labels about hair colors ) - subsampled the full dataset by $$1 / 20$$ ( while maintaining the imbalance ratio $$\rho \approx 10.7$$ ) - denote the resulting dataset by CelebA-5.
Twitter & Reuters : - from NLP - also evaluate our method on them to test the effectiveness under much extreme imbalance. - Imbalance ratio $$N_1 / N_k$$ of these two datasets are about 150 and 710 , ( much higher than the other image datasets ) - Reuters : exclude the classes having less than 5 samples in the test set for more reliable evaluation, resulting a dataset of 36 classes.
### Results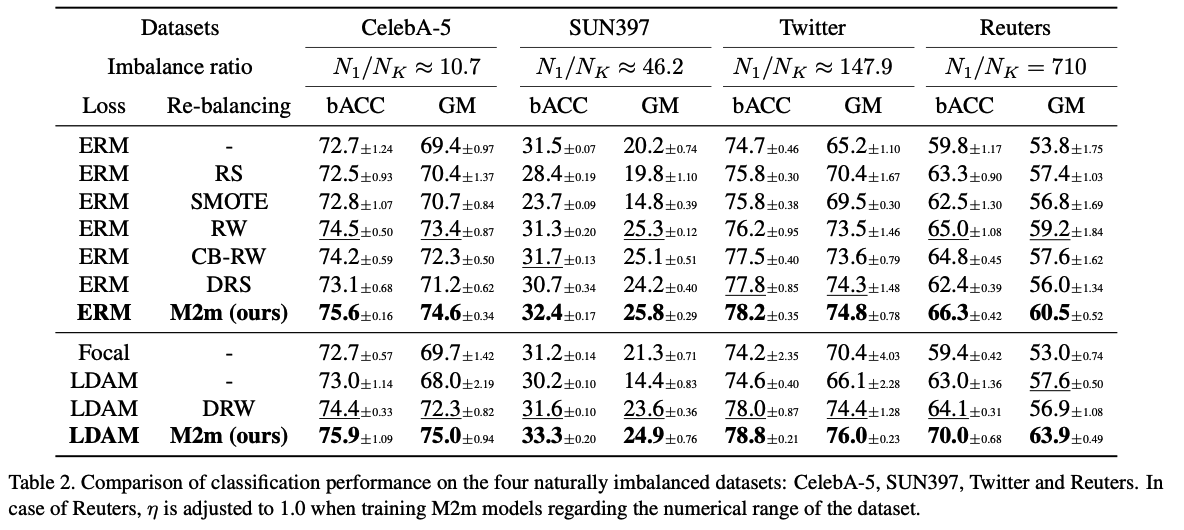 
## (4) Ablation Study Settings - ResNet-32 models, - trained on CIFAR-LT-10 with the imbalance ratio $$\rho=$$ 100. - additionally report the balanced test accuracy over majority & minority classes, - majority classes = top- $$k$$ frequent classes ( in training dataset ) - where $$k$$ is the minimum number that $$\sum_k N_k$$ exceeds $$50 \%$$ of the total. - minority classes = remaining classes.
### a) Diversity on seed samples. Effectiveness of our method mainly comes from **utilizing a much diversity in the majority samples** to prevent the over-fitting to the minority classes. $$\rightarrow$$ Verify with ablation study!!
Setting : Candidates of "seed samples" are limited - control the size of seed sample pools per each class to a fixed subset of the training set, made before training $$f$$.
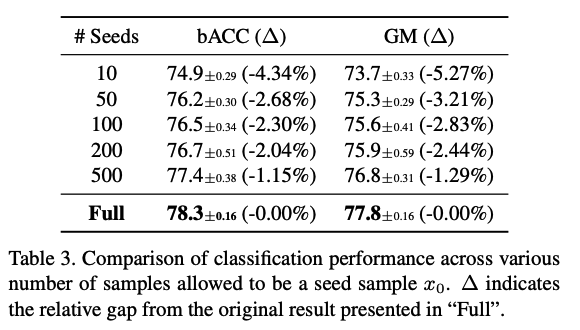 - accuracy of minority samples is increrased as **seed sample pools become diverse**
### b) Effect of $$\lambda$$ Regularization term $$\lambda \cdot f_{k_0}(x)$$ - to improve the quality of synthetic samples - they might confuse $$f$$ if themselves still contain important features of the original class in a viewpoint of $$f$$.
To verify the effect of this term.... - ablation that $$\lambda$$ is set to 0 , - certain level of degradation in the balanced test accuracy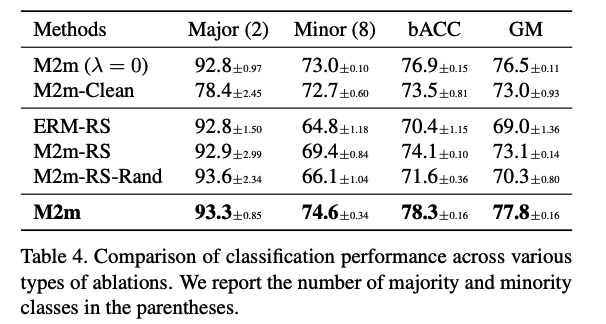 
### c) Over-sampling from the scratch "Deferred" scheduling to our method by default - start to apply our method after the standard ERM training for a fixed number of epochs.
Ablation where this strategy is not used = "M2m-RS" ( shown in Table 4 )
### d) Labeling as a targeted class Primary assumption on the pre-trained classifier $$g$$ : - does not require that $$g$$ itself to generalize well on the minority classes $$\rightarrow$$ may not end up with a synthetic sample that contains generalizable features of the target minority class.
Examine how much the generated samples would be correlated to the target classes - instead of labeling the generated sample as the target class, the ablated method "M2m-RS-Rand" labels it to a "random" class ( except for target & original classes ) ( shown in Table 4 ) $$\rightarrow$$ correctly-labeled synthetic samples could improve the generalization of the minority classes.
### e) Comparison of t-SNE embeddings 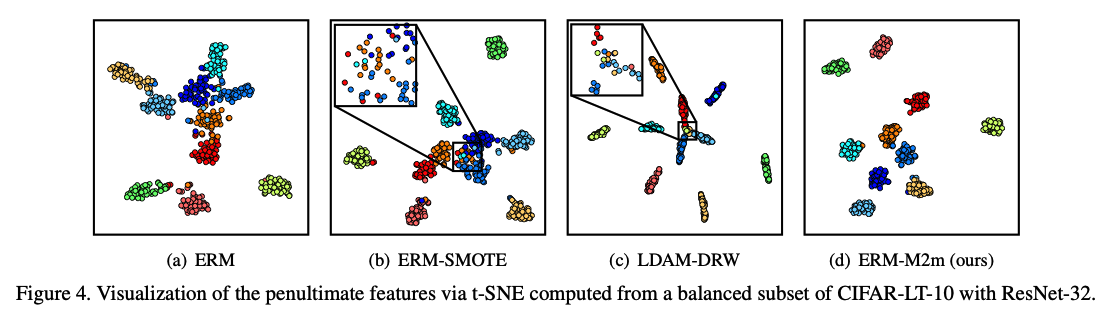 Randomly-chosen subset of training samples in the CIFAR-LT-10 $$(\rho=100)$$, - 50 samples per each class.
### f) Comparison of cumulative FP Number of false positive (FP) samples increases as summed over classes, namely $$\sum_k \mathrm{FP}_k$$, from the most frequent class to the least one - $$\mathrm{FP}_k$$ : the number of misclassified samples by predicting them to class $$k$$ in the test set.
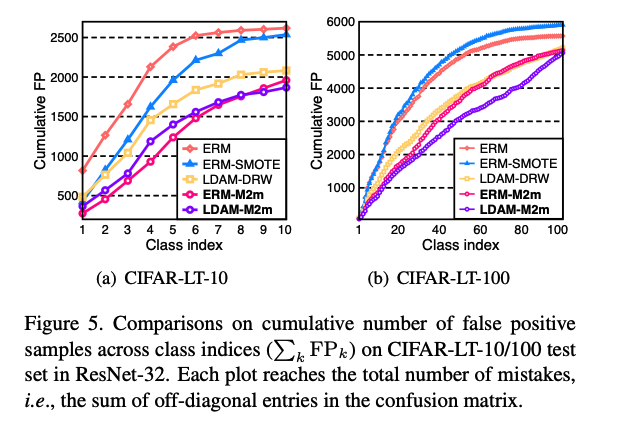 M2m makes less false positives, and even better, they are more uniformly distributed over the classes.
### g) The use of adversarial examples. Generation under M2m : $$\rightarrow$$ often ends up with a synthetic minority sample that is **very close to the original** ( = like adversarial example ) - This happens when $$f$$ and $$g$$ are NNs
To see **adversarial perturbations effect ** ... perform ablation study - (original) synthesizes a minority sample $$x^*$$ from a seed majority sample $$x_0$$. - (M2m-Clean) uses the "clean" $$x_0$$ instead of $$x^*$$ for over-sampling
( shown in Table 4 ) - adversarial perturbations ablated are extremely crucial !!
# 4. Conclusion Major-to-minor Translation (M2m) : - new over-sampling method for imbalanced classification Diversity in majority samples could much help the class-imbalanced training, even with a simple translation method using a pre-trained classifier. Lead us to an essential question that whether an adversarial perturbation could be a good feature. $$\rightarrow$$ YES !