(paper) Domain-Adversarial Training of Neural Networks

Domain-Adversarial Training of Neural Networks ( 2015, 4320 )

Contents

1. Abstract
2. Introduction
3. Domain Adaptation
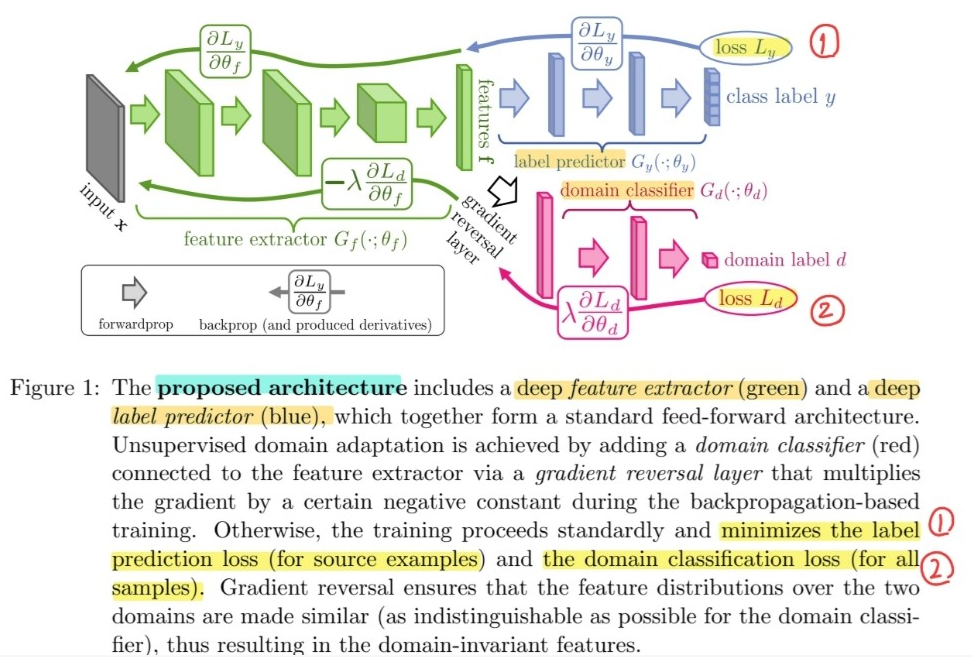
4. DANN (Domain Adaptation NN)

0. Abstract

data at train & test time : “different distn”

• train = SOURCE domain
  • labeled data
• test = TARGET domain
  • unlabeled ( or few-labeled ) data

Features :

• 1) “discriminative” for main learning task ( on source domain )
• 2) “indiscriminative” w.r.t shift between domains

Example ) used in…

• 1) document sentiment analysis
• 2) image classification

1. Introduction

Costly to generate labeled data!

Domain Adaptation (DA)

• learning a discriminative predictor, in the presence of “shift between train/test distributions”
• mapping between domains, where target domain data are..
  • 1) fully unlabeled : UNSUPERVISED DA
  • 2) few-labeled : SEMI-SUPERVISED DA

This paper focus on learning features, that combine

• (1) discriminativeness
• (2) domain invariance

by using..

• 1) label predictor

  • MINIMIZE loss of label classifier

• 2) domain classifier

  • MAXIMIZE loss of domain classifier

  ( works adversarially )

\(\rightarrow\) encourages “domain invariant” features

2. Domain Adaptation

Notation

• \(X\) : input space
• \(Y=\{0,1, \ldots, L-1\}\) : set of \(L\) possible labels
• 2 different distributions over \(X \times Y\)
  • 1) Source domain : \(\mathcal{D}_{\mathrm{S}}\)
  • 2) Target domain : \(\mathcal{D}_{\mathrm{T}}\)

Unsupervised DA

• given…

  • 1) \(n\) labeled source samples … \(S \sim \mathcal{D}_{\mathrm{S}}\)

  • 2) \(n^{'}\) unlabeled target samples … \(T \sim \mathcal{D}_{\mathrm{T}}^{X}\)

    ( \(\mathcal{D}_{\mathrm{T}}^{X}\) = marginal distn of \(\mathcal{D}_{\mathrm{T}}\) over \(X\) )

• notation

  • \(S=\left\{\left(\mathbf{x}_{i}, y_{i}\right)\right\}_{i=1}^{n} \sim\left(\mathcal{D}_{\mathrm{S}}\right)^{n}\).
  • \(T=\left\{\mathbf{x}_{i}\right\}_{i=n+1}^{N} \sim\left(\mathcal{D}_{\mathrm{T}}^{X}\right)^{n^{\prime}}\).
  • total # of data : \(N = n+n^{'}\).

• Goal

  • build a classifier \(\eta: X \rightarrow Y\),

    with a low target risk : \(R_{\mathcal{D}_{\mathrm{T}}}(\eta)=\operatorname{Pr}_{(\mathrm{x}, y) \sim \mathcal{D}_{\mathrm{T}}}(\eta(\mathrm{x}) \neq y)\)

(1) Domain Divergence

( several notions of distance have been proposed for DA )

Goal :

• minimize “target domain error”

• upper bound of target domain error

  = “source domain error” + “domain divergence”

\(\rightarrow\) (1) classify well in source domain & (2) minimize domain divergence

a) \(\mathcal{H}\) - divergence

• \(d_{\mathcal{H}}\left(\mathcal{D}_{\mathrm{S}}^{X}, \mathcal{D}_{\mathrm{T}}^{X}\right)=2 \sup _{\eta \in \mathcal{H}} \mid \underset{\mathbf{x} \sim \mathcal{D}_{\mathrm{S}}^{X}}{\operatorname{Pr}}[\eta(\mathbf{x})=1]-\underset{\mathbf{x} \sim \mathcal{D}_{\mathrm{T}}^{X}}{\operatorname{Pr}}[\eta(\mathbf{x})=1] \mid\).

b) empirical \(\mathcal{H}\) - divergence

• \(\hat{d}_{\mathcal{H}}(S, T)=2\left(1-\min _{\eta \in \mathcal{H}}\left[\frac{1}{n} \sum_{i=1}^{n} I\left[\eta\left(\mathbf{x}_{i}\right)=0\right]+\frac{1}{n^{\prime}} \sum_{i=n+1}^{N} I\left[\eta\left(\mathbf{x}_{i}\right)=1\right]\right]\right)\).

3. DANN (Domain Adaptation NN)