[Explicit DGM] 05. CVAE & VaDE

[Explicit DGM] 05. Conditional VAE

( 참고 : KAIST 문일철 교수님 : 한국어 기계학습 강좌 심화 2)

Contents

1. Conditional VAE (CVAE)
2. Variational Deep Embedding (VaDE)

1. Conditional VAE (CVAE)

VAE vs Conditional VAE (CVAE)

• VAE : label 정보를 활용하지 않는다.

• Conditional VAE : label 정보를 활용 한다

  ( 조건으로써 활용하여, 원하는 조건의 데이터를 생성한다 )

ELBO

• (VAE의 ELBO)

  • \(\mathcal{L}=-D_{K L}\left(q_{\phi}(h \mid e) \mid \mid p_{\theta}(h )\right)+\mathbb{E}_{q_{\phi}}(h \mid e)\left[\log p_{\theta}(e \mid h)\right]\).

• (Cond VAE의 ELBO)

  • \(\mathcal{L}=-D_{K L}\left(q_{\phi}(h \mid e, y) \mid \mid p_{\theta}(h \mid y)\right)+\mathbb{E}_{q_{\phi}}(h \mid e, y)\left[\log p_{\theta}(e \mid y, h)\right]\).

    • \(p_{\theta}(e \mid y, h):\) Decoder

    • \(q_{\phi}(h \mid e, y):\) Encoder

      \(\rightarrow\) 이 둘 다, \(y\) 라는 label 정보 ( conditional variable) 를 활용하는 것을 알 수 있다!

2. Variational Deep Embedding (VaDE)

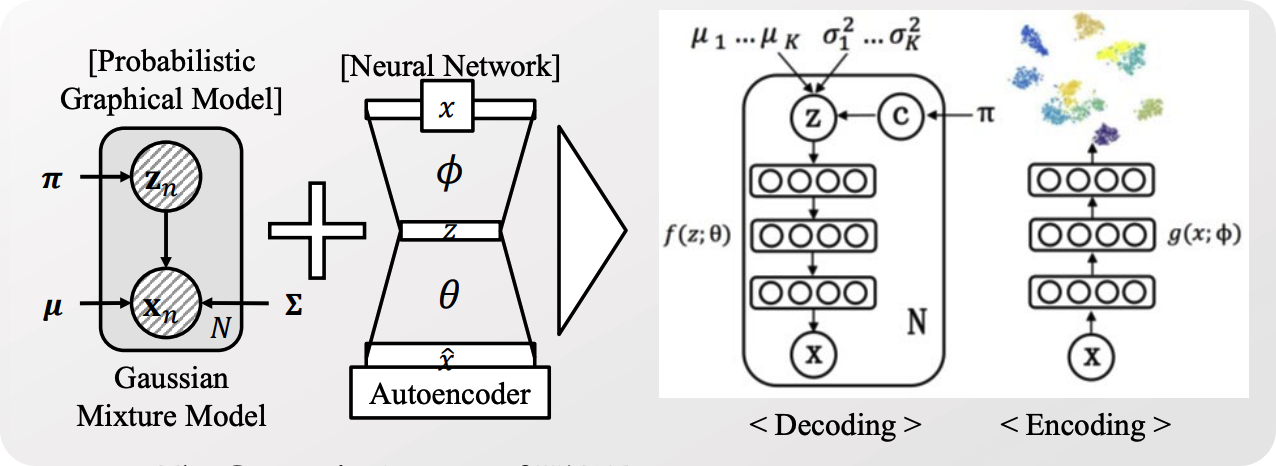
위 그림을 간단히 소개하자면…

1. Encoder

   • x가 들어가서, \(K\) 개의 군집에 해당하는 latent variable들을 전부 생성한다

     ( \(\mu_1 \cdots \mu_k\) & \(\sigma_1^2 \cdots \sigma_k^2\) )

2. Decoder

   • ( 파라미터 \(\pi\) 를 가지는 ) categorical distn \(c\)에서, cluster assignment를 샘플한다.
   • 해당 cluster에 해당하는 \(\mu\) 와 \(\sigma^2\) 를 가지고서 \(z\) 를 샘플한다.
   • 해당 \(z\) 를 사용하여, deterministic하게 reconstruction을 한다.

(1) VaDE의 generative process

1. cluster를 샘플한다.
   • \(c \sim \operatorname{Cat}(\pi)\).
2. 샘플한 cluster에 해당하는 latent variable를 샘플한다.
   • \(\boldsymbol{h} \sim \mathcal{N}\left(\boldsymbol{\mu}_{c}, \boldsymbol{\sigma}_{c}^{2} \boldsymbol{I}\right)\),
3. 샘플한 latent variable을 사용하여, 데이터(\(e\)) 를 샘플한다.
   • (binary의 경우) \(\mathbf{e} \sim \operatorname{Ber}\left(\boldsymbol{\mu}_{e}\right)\)
   • (real-value의 경우) \(\mathbf{e} \sim \mathcal{N}\left(\boldsymbol{\mu}_{e}, \boldsymbol{\sigma}_{e}^{2} \boldsymbol{I}\right)\)

(2) Probabilistic Modeling of VaDE

VAE & CVAE & VaDE 의 ELBO & posterior 비교

(1) ELBO

• (VAE) \(\mathcal{L}=-D_{K L}\left(q_{\phi}(h \mid e) \mid \mid p_{\theta}(h)\right)+\mathbb{E}_{q_{\phi}(h \mid e)}\left[\log p_{\theta}(e \mid h)\right]\)
• (CVAE) \(\mathcal{L}=-D_{K L}\left(q_{\phi}(h \mid e, y) \mid \mid p_{\theta}(h \mid y)\right)+\mathbb{E}_{q_{\phi}(h \mid e, y)}\left[\log p_{\theta}(e \mid y, h)\right]\)
• (VaDE) 아래 참고

(2) Posterior

• (VAE) \(q_{\phi}(\boldsymbol{h} \mid \boldsymbol{e})=\mathcal{N}\left(\boldsymbol{h} ; \boldsymbol{\mu} , \boldsymbol{\sigma}^{2} \boldsymbol{I}\right)\).
  • \(\mu=N N_{\mu}(e)\).
  • \(\log \sigma=N N_{\sigma}(e)\).
• (CVAE) \(q_{\phi}(h \mid e, y)=\mathcal{N}\left(\boldsymbol{h} ; \boldsymbol{\mu}, \boldsymbol{\sigma}^{2} \boldsymbol{I}\right)\).
  • \(\mu=N N_{\mu}(e, y)\),
  • \(\log \sigma=N N_{\sigma}(e, y)\),
• (VaDE) 아래 참고

[VaDE] ELBO

\(\begin{aligned} \log p(\boldsymbol{e})&=\log \int_{h} \sum_{c} p(\mathbf{e}, \mathrm{h}, c) d \mathrm{~h} \\ &\geq \mathbb{E}_{q(\mathrm{~h}, c \mid \mathrm{e})}\left[\log \frac{p(\mathrm{e}, \mathrm{h}, c)}{q(\mathrm{h}, c \mid \mathrm{e})}\right]=\mathcal{L}_{E L B O} \end{aligned}\).

\(\begin{aligned} \mathcal{L}_{E L B O}(\boldsymbol{e})&=\mathbb{E}_{q(\mathrm{h}, c \mid \mathrm{e})}\left[\log \frac{p(\mathrm{e}, \mathrm{h}, c)}{q(\mathrm{h}, c \mid \mathrm{e})}\right] \\&=\mathbb{E}_{q(\mathrm{~h}, c \mid e)}[\log p(\mathrm{e}, \mathrm{h}, c)-\log q(\mathrm{h}, c \mid e)] \\ &=\mathbb{E}_{q(\mathrm{h}, c \mid \mathrm{e})}[\log p(\mathrm{e} \mid h)+\log p(\mathrm{h} \mid c)+\log p(c)-\log q(\mathrm{h} \mid \mathrm{e})-\log q(c \mid e)] \end{aligned}\).

[VaDE] Posterior

\(q_{\phi}(\boldsymbol{h}, c \mid \mathbf{e}) \approx q_{\phi}(\boldsymbol{h} \mid \mathbf{e}) q_{\phi}(c \mid \mathbf{e})\).

• \(q_{\phi}(\boldsymbol{h} \mid \boldsymbol{e})=\mathcal{N}\left(\boldsymbol{h} ; \tilde{\mu}, \tilde{\sigma}^{2} \boldsymbol{I}\right)\).
  • \(\tilde{\mu}=N N_{\widetilde{\mu}}(e)\).
  • \(\log \tilde{\sigma}=N N_{\widetilde{\sigma}}(e)\).
• \(q_{\phi}(c \mid \mathbf{e})\) : GMM에서 cluster assignment probability

( 구체적인 ELBO의 전개과정은 생략한다 )