[Paper Review] 12.(conditioning) Generative Adversarial Text to Image Synthesis

[Paper Review] 12. Generative Adversarial Text to Image Synthesis

Contents

1. Abstract
2. Introduction
3. Background
   1. GAN
   2. Deep symmetric structured joint embedding
4. Method
   1. Network Architecture
   2. GAN-CLS ( Matching-aware discriminator )
   3. GAN-INT ( Learning with manifold interpolation )

0. Abstract

“Image synthesis from TEXT”

• a) use of RNN to extract text feature representation
• b) use of GAN to generate images

1. Introduction

interested in translating text in the form of “single sentence” into “image pixels”

challenging problems

• 1) learn text feature representation that captures the important visual details
• 2) use these features to synthesize a compelling image

\(\rightarrow\) use DL to solve these problems!

DIFFICULT ISSUE : distn of images, conditioned on text description is HIGHLY MULTIMODAL

( there are many plausible configurations of pixels that corresponds to that description )

\(\rightarrow\) conditioning both G & D on side information!

Contribution

develop a simple & effective GAN architecture & training strategy,

that enables compelling text to image synthesis of bird/flower… images

2. Background

2-1. GAN

\(\min _{G} \max _{D} V(D, G)= \mathbb{E}_{x \sim p_{\text {data }}(x)}[\log D(x)]+ \mathbb{E}_{x \sim p_{z}(z)}[\log (1-D(G(z)))]\).

2-2. Deep symmetric structured joint embedding

to obtain visually-discriminative vector representation of text….

\(\rightarrow\) use Deep Convolutional &Recurrent Text Encoders

Text Classifier \(f_{t}\)

• loss function : \(\frac{1}{N} \sum_{n=1}^{N} \Delta\left(y_{n}, f_{v}\left(v_{n}\right)\right)+\Delta\left(y_{n}, f_{t}\left(t_{n}\right)\right)\).
  • \(\left\{\left(v_{n}, t_{n}, y_{n}\right): n=1, \ldots, N\right\}\) : training data
  • \(\Delta\) : 0-1 loss
  • \(v_{n}\) : images
  • \(t_{n}\) : texts
  • \(y_{n}\) : class labels

Classifiers are parameterized as…

• \(f_{v}(v) =\underset{y \in \mathcal{Y}}{\arg \max } \mathbb{E}_{t \sim \mathcal{T}(y)}\left[\phi(v)^{T} \varphi(t)\right]\).
• \(f_{t}(t) =\underset{y \in \mathcal{Y}}{\arg \max } \mathbb{E}_{v \sim \mathcal{V}(y)}\left[\phi(v)^{T} \varphi(t)\right]\).
  • \(\phi\) : image encoder
  • \(\varphi\) : text encoder
  • \(\mathcal{T}(y)\) : set of text descriptions of \(y\)
  • \(\mathcal{V}(y)\) : set of image descriptions of \(y\)

3. Method

approach : train DCGAN conditioned on text features

( encoded by hybrid character-level Convolutional Reccurent NN )

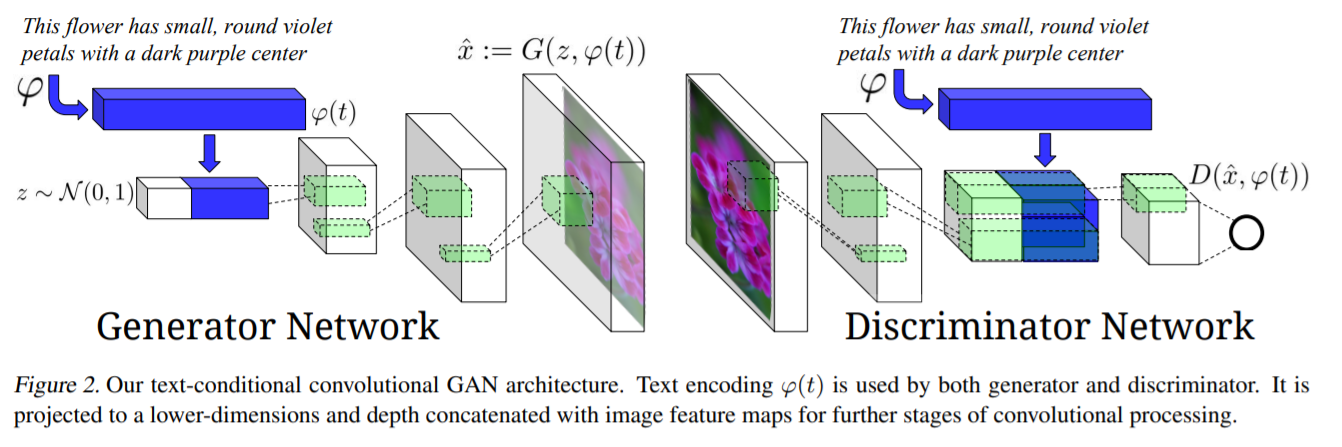
3-1. Network Architecture

Generator ( \(G: \mathbb{R}^{Z} \times \mathbb{R}^{T} \rightarrow \mathbb{R}^{D}\) )

• sample \(z \in \mathbb{R}^{Z} \sim \mathcal{N}(0,1)\)
• encode text \(t\) using \(\varphi\)
  • compressed using FC layer & leaky-ReLU
  • then, concatenated to \(z\)
• synthetic image : \(\hat{x} \leftarrow G(z, \varphi(t))\).

Discriminator ( \(\mathbb{R}^{D} \times \mathbb{R}^{T} \rightarrow\{0,1\}\) )

• perform several layers of stride 2 convolution with spatial batch normalization
• reduce the dimensionality of \(\varphi(t)\)

3-2. GAN-CLS ( Matching-aware discriminator )

view (text, image) pairs as joint observation

& train discriminator to judge pair as real/fake

[1] Beginning of training ….

• \(D\) ignores conditioning info
• easily rejects samples from \(G\)

[2] After \(G\) has learned to generate plausible images…

• \(G\) must also learn to align them with conditioning info
• \(D\) must learn to evaluate whether samples from \(G\) meet this condition

Naive GAN

• two inputs of \(D\) :

  • 1) real images ( with matching texts )
  • 2) synthetic images ( with arbitrary texts )

• two sources of error

  • 1) unrealistic images ( for ANY text )
  • 2) realistic images ( of the WRONG class )

  \(\rightarrow\) modify the GAN training to separate these error sources

Modified GAN

• add third type of input to \(D\)!

  • consisting of “real images with mismatched text”

    ( \(D\) should learn to score as “fake” )

Algorithm

3-3. GAN-INT ( Learning with manifold interpolation )

we can generate large amount of additional text embeddings…

by simply interpolating between embeddings

( = need not correspond to any actual human-written text )

can be viewed as adding an additional term to \(G\) to minimize…

• \(\mathbb{E}_{t_{1}, t_{2} \sim p_{\text {data }}}\left[\log \left(1-D\left(G\left(z, \beta t_{1}+(1-\beta) t_{2}\right)\right)\right)\right]\).

since interpolated embeddings are synthetic…

\(\rightarrow\) \(D\) does not have “real” corresponding images

“However, \(D\) learns to predict whether image and text pairs match or not. Thus, if \(D\) does a good job at this, then by satisfying \(D\) on interpolated text embeddings \(G\) can learn to fill in gaps on the data manifold in between training points”