[Paper Review] 15.(G arch) Image Generators with Conditionally-Independent Pixel Synthesis

[Paper Review] 15. Image Generators with Conditionally-Independent Pixel Synthesis

Contents

1. Abstract
2. Introduction
3. Method
   1. Positional Encoding (PE)

0. Abstract

Most of existing GAN …. rely on spatial convolutions ( + self-attention blocks )

Present a new architecture for image generator!

• color value AT EACH PIXEL is computed INDEPENDENTLY,

  given the value of (1) random latent vector & (2) coordinate of that pixel

• NO spatial convolutions

1. Introduction

Recently, some architectures WITHOUT spatial convolutions have been suggested

\(\rightarrow\) HOWEVER,, restricted to individual scenses

This paper designed & trained deep generative architectures for diverse classes of images that achieve similar quality of StyleGANv2 … called CIPS ( = Conditionally-Independent Pixel Synthesis )

2. Method

CIPS synthesize images of fixed resolution \(H \times W\)!

Input

• 1) random vector \(\mathbf{z} \in \mathcal{Z}\)
• 2) pixel coordinates \((x, y) \in \{0 \ldots W-1\} \times\{0 \ldots H-1\}\)

Mapping

• \(G:(x, y, \mathbf{z}) \mapsto \mathbf{c}\).

  where RGB value \(\mathbf{c} \in[0,1]^{3}\)

To compute whole input image \(I\),….

• \(G\) is evaluated at each pair \((x,y)\) of grid, while keeping \(\mathbf{z}\) fixed!
• \(I=\{G(x, y ; \mathbf{z}) \mid(x, y) \in \operatorname{mgrid}(H, W)\}\).
  • where \(\operatorname{mgrid}(H, W)=\{(x, y) \mid 0 \leq x<W, 0 \leq y<H\}\).

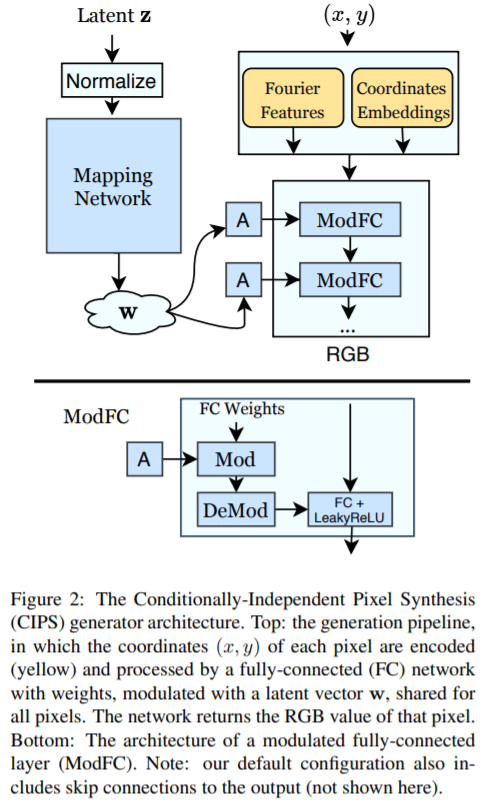
[ Similar to StyleGAN ]

mapping network \(M\)

• style vector \(\mathbf{w} \in \mathcal{W}, M: \mathbf{z} \mapsto \mathbf{w}\).

StyleGANv2

• use weight modulation
• ModFC (= Modulated Fully-Connected) : \(\psi \in \mathbb{R}^{m}=\hat{B} \phi+\mathbf{b}\)
  • \(\psi \in \mathbb{R}^{m}\) : output
  • \(\phi \in \mathbb{R}^{n}\) : input
  • \(\hat{B}\) : learnable weight
    • \(\hat{B}_{i j}=\frac{s_{j} B_{i j}}{\sqrt{\epsilon+\sum_{k=1}^{n}\left(s_{k} B_{i k}\right)^{2}}}\).
      • \(B \in \mathbb{R}^{m \times n}\) : modulated with the style \(\mathbf{w}\)
      • scale vector \(\mathbf{s} \in \mathbb{R}^{n}\)
  • \(\mathbf{w}, \mathbf{b} \in \mathbb{R}^{m}\) : learnable bias

• After linear mapping, apply Leaky ReLU

• add skip connections for every 2 layers of intermediate feature maps

• PARALLELIZABLE at inference time

  ( \(\because\) independence of pixel generation process )

2-1. Positional Encoding (PE)

2 slightly different versions of PE

• 1) SIREN
  • perceptron with a principled weight initialization
  • activation function : sine
• 2) Fourier features

Proposed : use somewhat between 1) & 2)

• use sine function to obtain Fourier embedding \(e_{f o}\)

  • \(e_{f o}(x, y)=\sin \left[B_{f o}\left(x^{\prime}, y^{\prime}\right)^{T}\right]\).
    • where \(x^{\prime}=\frac{2 x}{W-1}-1\) and \(y^{\prime}=\frac{2 y}{H-1}-1\) are pixel coordinates

• [coordinate embeddings]

  • also train separate vector \(e_{c o}^{(x, y)}\) for each spatial position

• concatenate those two!

  • \(e(x, y)=\operatorname{concat}\left[e_{f o}(x, y), e_{c o}^{(x, y)}\right]\).

  • can be viewed as … \(G(x, y ; \mathbf{z})=G^{\prime}(e(x, y) ; M(\mathbf{z}))\)