[Paper Review] 16. InterFaceGAN : Interpreting the Disentangled Face Representation Learned by GANs
Contents
- Abstract
- Semantics in Latent Space
- Single Semantic
- Multiple Semantics
- Manipulation in Latent Space
- Single Attribute Manipulation
- Conditional Manipulation
0. Abstract
GAN lacks enough understanding, of what GANS have learned in latent representation
\(\rightarrow\) propose “InterFaceGAN”,
- to interpret the disentangled face representation, learned by SOTA models
(1) find that GANS learn various semantics in some linear subspaces of latent space
(2) after identifying these subspaces, realistically manipulate the corresponding facial attributes
1. Semantics in Latent Space
analysis of properties of the semantics, emerging in the latent representations
Notation
-
generator : \(g: \mathcal{Z} \rightarrow \mathcal{X}\)
-
semantic scoring function : \(f_{S}: \mathcal{X} \rightarrow \mathcal{S}\)
where \(\mathcal{S} \subseteq \mathbb{R}^{m}\) = semantic space with \(m\) semantics
Bridge the latent space \(\mathcal{Z}\) & semantic space \(\mathcal{S}\) with \(\mathrm{s}=f_{S}(g(\mathbf{z}))\),
- s = semantic scores
- \(\mathrm{z}\) = sampled latent coded
(1) Single Semantic
Interpolation
-
widely observed that when linearly interpolating two latent codes, \(\mathrm{z}_{1}\) and \(\mathrm{z}_{2}\)…
\(\rightarrow\) appearance of the synthesis changes continuously ( change gradually )
Assumption
-
for any binary semantic ( ex) male/female ),
there exists a HYPERPLANE in the latent space, serving as BOUNDARY
-
given a hyperplane with unit normal vector \(\mathbf{n} \in \mathbb{R}^{d}\),
define DISTANCE ( from \(\mathbf{z}\) ~ hyperplane ) as : \(\mathrm{d}(\mathbf{n}, \mathbf{z})=\mathbf{n}^{T} \mathbf{z}\)
-
it is just when the “distance” changes its numerical sign that the semantic attribute reverses
\(\rightarrow\) \(f(g(\mathbf{z}))=\lambda \mathrm{d}(\mathbf{n}, \mathbf{z})\)
- \(f(\cdot)\) : scoring function
- \(\lambda >0\) : measure “how fast semantic varies” along with the “change of distance”
(2) Multiple Semantics
case : \(m\) different semantics
Just Multivariate Version of (1) !
-
\[\mathbf{s} \equiv f_{S}(g(\mathbf{z}))=\Lambda \mathbf{N}^{T} \mathbf{z}.\]
- where \(\mathrm{s}=\left[s_{1}, \ldots, s_{m}\right]^{T}\)denotes semantic scores
- \(\operatorname{diag}\left(\lambda_{1}, \ldots, \lambda_{m}\right)\) : diagonal matrix with linear coefficients
- \(\mathbf{N}=\left[\mathbf{n}_{1}, \ldots, \mathbf{n}_{m}\right]\) : separation boundaries
\(\mathrm{s} \sim \mathcal{N}\left(\mathbf{0}, \boldsymbol{\Sigma}_{\mathrm{s}}\right)\).
-
mean of \(s\) :
- \(\mu_{\mathrm{s}} =\mathbb{E}\left(\Lambda \mathbf{N}^{T} \mathbf{z}\right)=\Lambda \mathbf{N}^{T} \mathbb{E}(\mathbf{z})=\mathbf{0}\).
-
covariance of \(s\) :
-
\(\boldsymbol{\Sigma}_{\mathbf{s}} =\mathbb{E}\left(\Lambda \mathbf{N}^{T} \mathbf{z} \mathbf{Z}^{T} \mathbf{N} \Lambda^{T}\right)=\Lambda \mathbf{N}^{T} \mathbb{E}\left(\mathbf{z} \mathbf{z}^{T}\right) \mathbf{N} \Lambda^{T} =\Lambda \mathbf{N}^{T} \mathbf{N} \Lambda\).
-
Different entries of s are disentangled if and only if \(\Sigma_{\mathrm{s}}\) is a diagonal matrix
\(\rightarrow\) requires \(\left\{\mathbf{n}_{1}, \ldots, \mathbf{n}_{m}\right\}\) to be orthogonal with each other
-
2. Manipulation in Latent Space
introduce how to use the semantics found in the latent space for image editing
(1) Single Attribute Manipulation
edit original latent code \(\mathbf{z}\) with….
- \(\mathrm{z}_{\text {edit }}=\mathrm{z}+\alpha \mathbf{n}\).
Ex) will make synthesis look more positive with that semantic, if \(\alpha >0\),
since \(f\left(g\left(\mathbf{z}_{\text {edit }}\right)\right)= f(g(\mathbf{z}))+\lambda \alpha\)
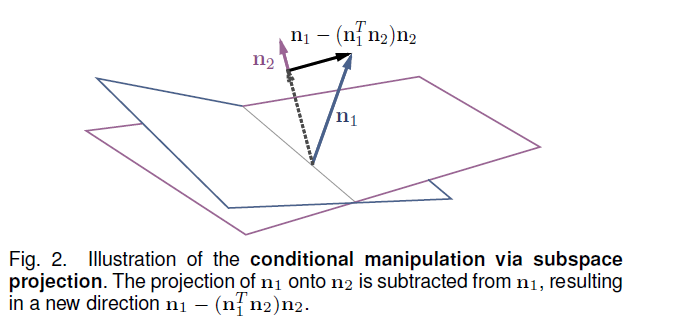
(2) Conditional Manipulation
when more than 1 attribute….
\(\rightarrow\) editing one may affect another! ( \(\because\) some semantics may be entagled )
for more precise control…propose CONDITIONAL manipulation
- by manually forcing \(\mathbf{N}^{T} \mathbf{N}\) to be diagonal
- use projection to make different vectors orthogonal!
Implementation Details
5 key facial attributes :
- pose / smile(expression) / age / gender / eyeglasses
