[ GAT, GraphSAGE Implementation ]
( 참고 : https://github.com/luciusssss/CS224W-Colab/blob/main/CS224W-Colab%203.ipynb )
Import packages
import torch
import torch_scatter
import torch.nn as nn
import torch.nn.functional as F
import torch_geometric.nn as pyg_nn
import torch_geometric.utils as pyg_utils
from torch import Tensor
from typing import Union, Tuple, Optional
from torch_geometric.typing import (OptPairTensor, Adj, Size, NoneType,
OptTensor)
from torch.nn import Parameter, Linear
from torch_sparse import SparseTensor, set_diag
from torch_geometric.nn.conv import MessagePassing
from torch_geometric.utils import remove_self_loops, add_self_loops, softmax
1. (package) GAT & GraphSAGE
class GNNStack(torch.nn.Module):
def __init__(self, input_dim, hidden_dim, output_dim, args, emb=False):
super(GNNStack, self).__init__()
conv_model = self.build_conv_model(args.model_type)
# 1) convolutional layers
## option : GraphSAGE / GAT
self.convs = nn.ModuleList()
self.convs.append(conv_model(input_dim, hidden_dim))
assert (args.num_layers >= 1), 'Number of layers is not >=1'
for l in range(args.num_layers-1):
self.convs.append(conv_model(args.heads * hidden_dim, hidden_dim))
# 2) post Message Passing
self.post_mp = nn.Sequential(
nn.Linear(args.heads * hidden_dim, hidden_dim),
nn.Dropout(args.dropout),
nn.Linear(hidden_dim, output_dim))
self.dropout = args.dropout
self.num_layers = args.num_layers
self.emb = emb
def build_conv_model(self, model_type):
if model_type == 'GraphSage':
return GraphSage
elif model_type == 'GAT':
return GAT
def forward(self, data):
x, edge_index, batch = data.x, data.edge_index, data.batch
for i in range(self.num_layers):
x = self.convs[i](x, edge_index)
x = F.relu(x)
x = F.dropout(x, p=self.dropout)
x = self.post_mp(x)
if self.emb == True:
return x
return F.log_softmax(x, dim=1)
def loss(self, pred, label):
return F.nll_loss(pred, label)
2. Implementation
(1) GraphSAGE
\[\begin{equation} h_v^{(l)} = W_l\cdot h_v^{(l-1)} + W_r \cdot AGG(\{h_u^{(l-1)}, \forall u \in N(v) \}) \end{equation}\]- 2 parts = central & neighbors
- aggregation : \(\begin{equation} AGG(\{h*_u^{(l-1)}, \forall u \in N(v) \}) = \frac{1}{ \mid N(v) \mid } \sum_*{u\in N(v)} h_u^{(l-1)} \end{equation}\)
propagate() = 1) + 2)
- 1)
message() - 2)
aggregate()
torch_scatter.scatter :
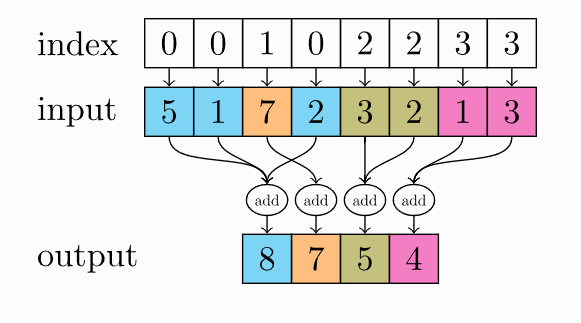
class GraphSage(MessagePassing):
def __init__(self, in_channels, out_channels, normalize = True,
bias = False, **kwargs):
super(GraphSage, self).__init__(**kwargs)
self.in_channels = in_channels
self.out_channels = out_channels
self.normalize = normalize
self.lin_l = nn.Linear(self.in_channels, self.out_channels) # 1) central node
self.lin_r = nn.Linear(self.in_channels, self.out_channels) # 2) neighbor node
self.reset_parameters()
def reset_parameters(self):
self.lin_l.reset_parameters()
self.lin_r.reset_parameters()
def forward(self, x, edge_index, size = None):
# 1) message passing [ PROPAGATE ]
## meaning of (x,x) = (central=neighbor)
prop = self.propagate(edge_index, x=(x, x), size=size)
# 2) message aggregation [ AGGREGATE ]
out = self.lin_l(x) + self.lin_r(prop)
# (normalization)
if self.normalize:
out = F.normalize(out, p=2) # L2-norm
return out
def message(self, x_j):
out = x_j
return out
def aggregate(self, inputs, index, dim_size = None):
node_dim = self.node_dim
out = torch_scatter.scatter(inputs, index, node_dim,
dim_size=dim_size, reduce='mean')
return out
(2) GAT
(Notation) GAT layer
- input : \(\mathbf{h} = \{\overrightarrow{h_1}, \overrightarrow{h_2}, \dots, \overrightarrow{h_N}\)} …….. \(\overrightarrow{h_i} \in R^F\)
- output : \(\mathbf{h'} = \{\overrightarrow{h_1'}, \overrightarrow{h_2'}, \dots, \overrightarrow{h_N'}\}\) ……. \(\overrightarrow{h_i'} \in \mathbb{R}^{F'}\)
- weight :
- \(\mathbf{W} \in \mathbb{R}^{F' \times F}\)…..\(\mathbf{W_l}\) & \(\mathbf{W_r}\)
Attention in GAT Layer
-
(general) attention :
- \(e_{ij} = a(\mathbf{W_l}\overrightarrow{h_i}, \mathbf{W_r} \overrightarrow{h_j})\) …… \(a : \mathbb{R}^{F'} \times \mathbb{R}^{F'} \rightarrow \mathbb{R}\)
- (advanced) attention :
- \(e_{ij} =\text{LeakyReLU}\Big(\overrightarrow{a_l}^T \mathbf{W_l} \overrightarrow{h_i} + \overrightarrow{a_r}^T\mathbf{W_r}\overrightarrow{h_j}\Big)\) ….. \(\overrightarrow{a} \in \mathbb{R}^{F'}\)
- denote \(\alpha_l = [...,\overrightarrow{a_l}^T \mathbf{W_l} \overrightarrow{h_i},...]\) and \(\alpha_r = [..., \overrightarrow{a_r}^T \mathbf{W_r} \overrightarrow{h_j}, ...]\).
- code
- \(\mathbf{W_l}\overrightarrow{h_i}\) :
x_l = self.lin_l(x).reshape(-1, H, C) - \(\mathbf{W_r} \overrightarrow{h_j}\) :
x_r = self.lin_r(x).reshape(-1, H, C) - \(\overrightarrow{a_l}^T \mathbf{W_l} \overrightarrow{h_i}\) :
alpha_l = self.att_l * x_l - \(\overrightarrow{a_r}^T\mathbf{W_r}\overrightarrow{h_j}\) :
alpha_r = self.att_r * x_r
- \(\mathbf{W_l}\overrightarrow{h_i}\) :
-
\(\alpha_{ij} = \text{softmax}_j(e_{ij}) = \frac{\exp(e_{ij})}{\sum_{k \in \mathcal{N}_i} \exp(e_{ik})}\).
( \(\alpha_{ij} = \frac{\exp\Big(\text{LeakyReLU}\Big(\overrightarrow{a_l}^T \mathbf{W_l} \overrightarrow{h_i} + \overrightarrow{a_r}^T\mathbf{W_r}\overrightarrow{h_j}\Big)\Big)}{\sum_{k\in \mathcal{N}_i} \exp\Big(\text{LeakyReLU}\Big(\overrightarrow{a_l}^T \mathbf{W_l} \overrightarrow{h_i} + \overrightarrow{a_r}^T\mathbf{W_r}\overrightarrow{h_k}\Big)\Big)}\) )
- code
- FORWARD
out = self.propagate(edge_index, x=(x_l, x_r), alpha=(alpha_l, alpha_r), size=size)- out : \(\overrightarrow{h_i}' = \mid \mid _{k=1}^K \Big(\sum_{j \in \mathcal{N}_i} \alpha_{ij}^{(k)} \mathbf{W_r}^{(k)} \overrightarrow{h_j}\Big)\).
- VALUE :
x=(x_l, x_r): \(\mathbf{W_l}\overrightarrow{h_i}\) & \(\mathbf{W_r} \overrightarrow{h_j}\) - WEIGHT :
alpha=(alpha_l, alpha_r): \(\overrightarrow{a_l}^T \mathbf{W_l} \overrightarrow{h_i}\) & \(\overrightarrow{a_r}^T\mathbf{W_r}\overrightarrow{h_j}\)
- MESSAGE
alpha = F.leaky_relu(alpha_i + alpha_j, negative_slope=self.negative_slope)- alpha = \(\text{LeakyReLU}\Big(\overrightarrow{a_l}^T \mathbf{W_l} \overrightarrow{h_i} + \overrightarrow{a_r}^T\mathbf{W_r}\overrightarrow{h_j}\Big)\)
- \(\overrightarrow{a_l}^T \mathbf{W_l} \overrightarrow{h_i}\) :
alpha_i - \(\overrightarrow{a_r}^T\mathbf{W_r}\overrightarrow{h_j}\) :
alpha_j
- FORWARD
- code
class GAT(MessagePassing):
def __init__(self, in_channels, out_channels, heads = 2,
negative_slope = 0.2, dropout = 0., **kwargs):
super(GAT, self).__init__(node_dim=0, **kwargs)
self.in_channels = in_channels
self.out_channels = out_channels
self.heads = heads
self.negative_slope = negative_slope
self.dropout = dropout
# 1) embedding layer
self.lin_l = nn.Linear(self.in_channels, self.out_channels * self.heads) # 1) central node
self.lin_r = self.lin_l # 2) neighbor node
# 2) (multi-head) attention layer
self.att_l = nn.Parameter(torch.zeros(self.heads, self.out_channels)) # 1) central node
self.att_r = nn.Parameter(torch.zeros(self.heads, self.out_channels)) # 2) neighbor node
self.reset_parameters()
def reset_parameters(self):
nn.init.xavier_uniform_(self.lin_l.weight)
nn.init.xavier_uniform_(self.lin_r.weight)
nn.init.xavier_uniform_(self.att_l)
nn.init.xavier_uniform_(self.att_r)
def forward(self, x, edge_index, size = None):
H, C = self.heads, self.out_channels
# 1) embedding ( + reshaping )
x_l = self.lin_l(x).reshape(-1, H, C)
x_r = self.lin_r(x).reshape(-1, H, C)
# 2) attention
alpha_l = self.att_l * x_l
alpha_r = self.att_r * x_r
# 3) message passing + aggregation
out = self.propagate(edge_index, x=(x_l, x_r),
alpha=(alpha_l, alpha_r), size=size)
out = out.reshape(-1, H*C)
return out
def message(self, x_j, alpha_j, alpha_i, index, ptr, size_i):
# 1) Final attention weights
alpha = F.leaky_relu(alpha_i + alpha_j, negative_slope=self.negative_slope)
# 2) Softmax ( over the neighbors )
if ptr:
att_weight = F.softmax(alpha, ptr)
else:
att_weight = torch_geometric.utils.softmax(alpha, index)
# 3) Dropout
att_weight = F.dropout(att_weight, p=self.dropout)
# 4) Embeddings X Attention weights
out = att_weight * x_j
return out
def aggregate(self, inputs, index, dim_size = None):
out = torch_scatter.scatter(inputs, index, self.node_dim,
dim_size=dim_size, reduce='sum')
return out
