(paper) Transfer GNN for pandemic forecasting

Transfer GNN for pandemic forecasting (2021)

Contents

1. Abstract
2. Methodlogy
   1. Graph Construction
   2. Models
      • MPNN
      • MPNN + LSTM
      • MPNN + TL

0. Abstract

Graph

• Node = country’s regions
• Edge = human mobility

\(\rightarrow\) use GNN to predict # of future cases

to account for limited training data…

• capitalize on the pandemic’s asynchronous outbreaks across countries
• use MAML (Model-Agnostic Meta Learning) based method to transfer knowledge from one country’s model to another

1. Methodlogy

Assumption

1. people who use FB on phones with Location History enabled,

   constitute a uniform random sample of the general population

2. # of cases in a region reported by the authorities is a representative sample of the number of people that have been actually infected by virus

3. the more people move from one region to another / within a region ,

   the higher probability that people in the receiving region are infected

(1) Graph Construction

\(G=(V, E)\).

• series of graph (by time) : \(G^{(1)}, \ldots, G^{(T)}\)
• single date’s mobility data \(\rightarrow\) into weighted & directed graph
  • ex) weight \(w_{v, u}^{(t)}\) of edge \((v, u)\) : # of people that moved from \(v\) to \(u\)
• can also contain self-loop
• node attribute : \(\mathbf{x}_{u}^{(t)}=\left(c_{u}^{(t-d)}, \ldots, c_{u}^{(t)}\right)^{\top} \in \mathbb{R}^{d}\)
  • # of cases for each one of the past \(d\) days in region \(u\)

Message Passing

computes a feature vector for each region, with a combined score from all regions

\(\mathbf{A}^{(t)} \mathbf{X}^{(t)}=\left[\begin{array}{cccc}w_{1,1}^{(t)} & w_{2,1}^{(t)} & \ldots & w_{n, 1}^{(t)} \\ w_{1,2}^{(t)} & w_{2,2}^{(t)} & \ldots & w_{n, 2}^{(t)} \\ \vdots & \vdots & \vdots & \vdots \\ w_{1, n}^{(t)} & w_{2, n}^{(t)} & \ldots & w_{n, n}^{(t)}\end{array}\right]\left[\begin{array}{c}\mathbf{x}_{1}^{(t)} \\ \mathbf{x}_{2}^{(t)} \\ \vdots \\ \mathbf{x}_{3}^{(t)}\end{array}\right]=\left[\begin{array}{c}\mathbf{z}_{1} \\ \mathbf{z}_{2} \\ \vdots \\ \mathbf{z}_{3}\end{array}\right]\).

• \(\mathbf{z}_{u} \in \mathbb{R}^{d}\) : vector that combines the mobility within and towards region \(u\) with the number of reported cases both in \(u\) and in all the other regions

stress the importance of the mobility patterns \(w_{u, u}\)

• good indicators of the evolution of the disease

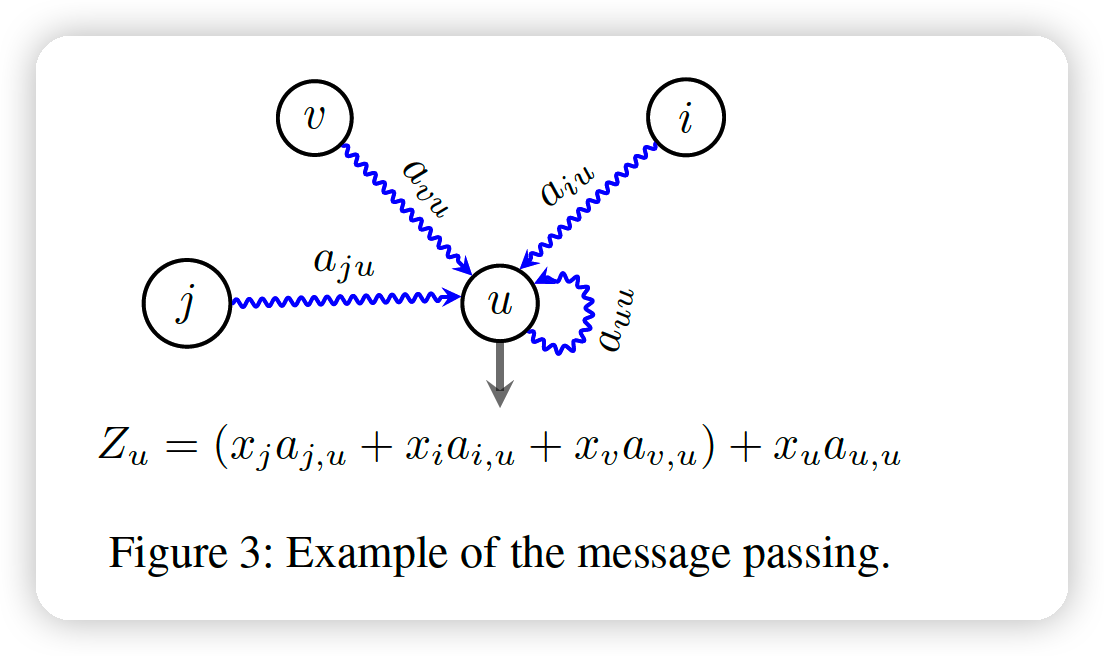
[ FIGURE ]

• toy example with a region \(u\) receiving \(a\) people from different regions,

• \(x\) : contain a vector of past cases in that region
• \(Z_{u} \in \mathbb{R}^{d}\) : an estimate of the number of new latent cases in \(u\)

(2) Models

MPNN ( Message Passing NN )

\(\mathbf{H}^{i+1}=f\left(\tilde{\mathbf{A}} \mathbf{H}^{i} \mathbf{W}^{i+1}\right)\).

• \(\mathbf{H}^{0}=\mathbf{X}, \mathbf{W}^{i}\).
• input graphs : \(G^{(1)}, \ldots, G^{(T)}\).
• \(K\) neighborhood aggregation layers
• matrices \(\tilde{\mathbf{A}}\) and \(\mathbf{H}^{0}, \ldots, \mathbf{H}^{K}\) are specific to a single graph
• \(\mathbf{W}^{1}, \ldots, \mathbf{W}^{K}\) are shared across all graphs

\(\mathbf{H}=\operatorname{CONCAT}\left(\mathbf{H}^{0}, \mathbf{H}^{1}, \mathbf{H}^{2}, \ldots, \mathbf{H}^{K}\right)\).

• concatenate the matrices \(\mathbf{H}^{0}, \mathbf{H}^{1}, \mathbf{H}^{2}, \ldots, \mathbf{H}^{K}\) horizontally

Loss Function : \(\mathcal{L}=\frac{1}{n T} \sum_{t=1}^{T} \sum_{v \in V}\left(y_{v}^{(t+1)}-\hat{y}_{v}^{(t+1)}\right)^{2}\)

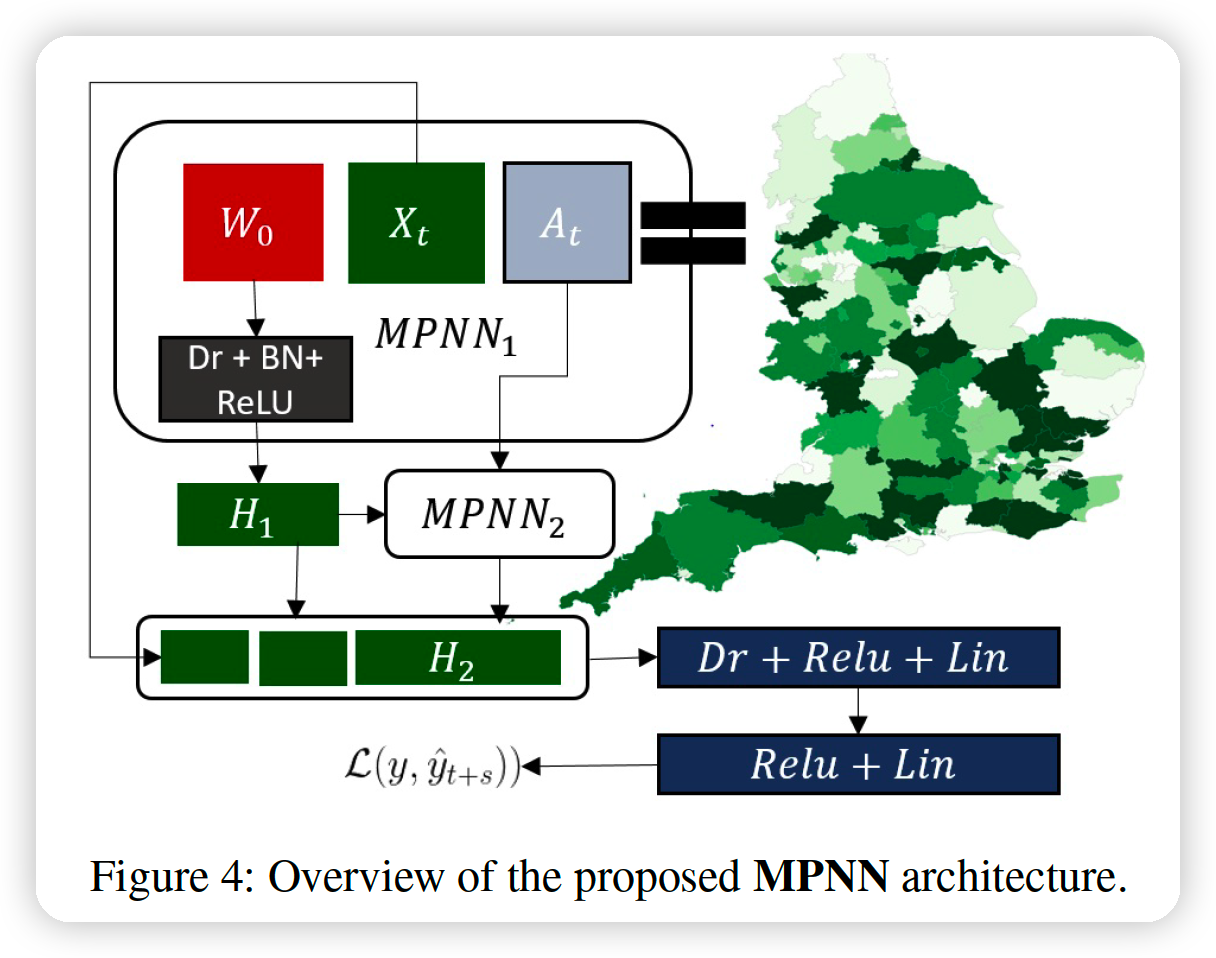
MPNN + LSTM

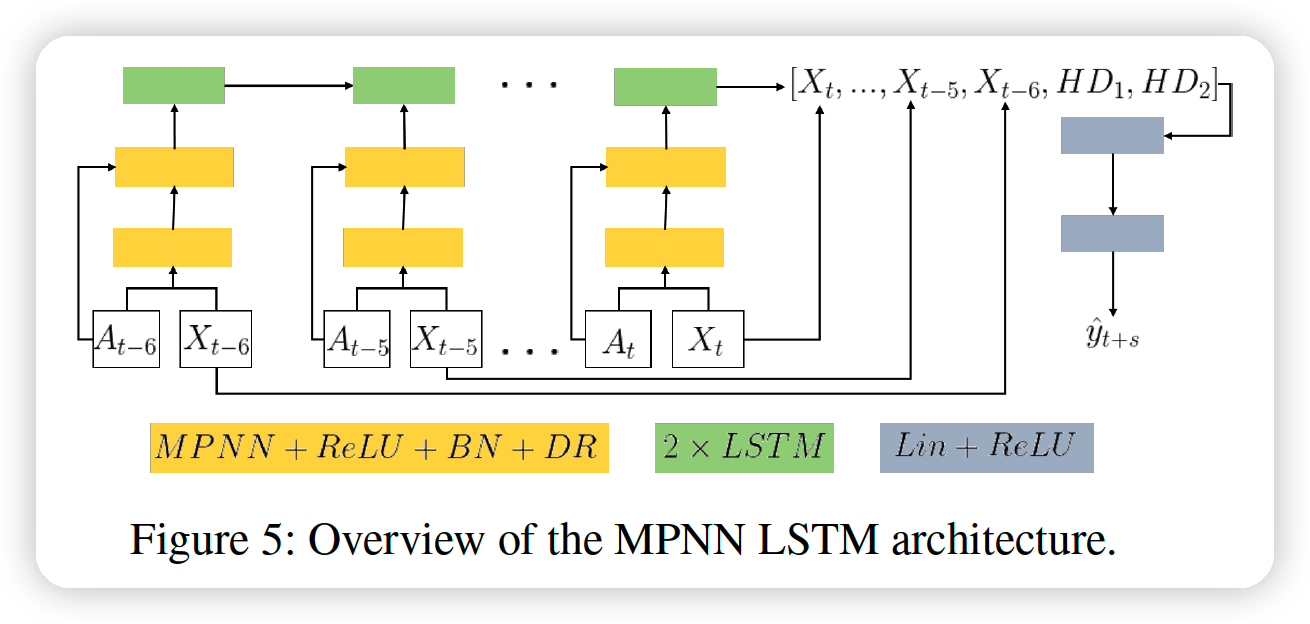
MPNN + TL

different countries = hit by pandameic at different times

\(\rightarrow\) might give additional info!

Model starts predicting as early as the 15th day of the dataset

To incorporate PAST KNOWLEDGE from models from other countires,

separate our data into tasks & propose an adaptation of MAML

Dataset

• meta train set : \(M_{\text {tr }}=\left\{D^{(1)}, \ldots, D^{(p)}\right\}\)
  • \(p\) countries
  • obtain paramterers \(\theta\)
• meta test set : \(M_{\text {te }}\)
  • initialize with learned \(\theta\)
• each dataset \(D^{(k)}, k \in\{1, \ldots, p\}\) is divided into subtasks itself
  • each country has different training sets

Model

• for each combination of 2,

  trian a different model!

• set of tasks for country \(k\) : \(D^{(k)}=\left\{\left(\operatorname{Tr}_{i, j}^{(k)}, T e_{i, j}^{(k)}\right): 14 \geq i \geq T_{\max }, 1 \geq j \geq d t\right\}\)

  • \(\left(T r_{i, j}^{(k)}, T e_{i, j}^{(k)}\right)\) : dataset associated with country \(k\)
    • train : first \(i\) days
    • task : predict the number of cases in the \(j\)-th day ahead.

in MAML……

• \(\theta\) is randomly initialized

• underoges gradient descent steps during the metatrain phase

• In each task…

  • minimize the loss on the task’s train set towards a task specific \(\theta_{t}\)

    ( \(\theta_{t} =\theta-\alpha \nabla_{\theta} \mathcal{L}\left(f_{\theta}\left(T r_{i, j}^{(k)}\right)\right)\) )

  • use \(\theta_{t}\) to compute the gradient with respect to \(\theta\) in the task’s test

    ( \(\theta =\theta-\alpha_{m} \nabla_{\theta} \mathcal{L}\left(f_{\theta_{t}}\left(T e_{i, j}^{(k)}\right)\right)\) )