Virtual Adversarial Training: A Regularization Method for Supervised and Semi-Supervised Learning (2017)
Contents
- Abstract
- Methods
- Adversarial Training
- Virtual Adversarial Training (VAT)
0. Abstract
new regularization method, based on virtual adversarial loss
virtual adversarial loss :
- measure of local smoothness of the conditional label distn, given input
- robustness of conditional label distn around each input against local perturbation
1. Methods
Notation
- input vector : \(x \in R^I\)
- output label : \(y \in Q\)
- output distn ( parameterized by \(\theta\) ) : \(p(y \mid x, \theta)\)
- \(\hat{\theta}\) : parameter at specific iteration step
- labeled/unlabeled dataset :
- (labeled) \(\mathcal{D}_l=\left\{x_l^{(n)}, y_l^{(n)} \mid n=1, \ldots, N_l\right\}\)
- (unlabeled) \(\mathcal{D}_{u l}=\left\{x_{u l}^{(m)} \mid m=1, \ldots, N_{u l}\right\}\)
Goal : train model \(p(y \mid x, \theta)\) using \(\mathcal{D}_l\) and \(\mathcal{D}_{u l}\)
(1) Adversarial Training
Loss function of adversarial training :
\(\begin{array}{r} L_{\mathrm{adv}}\left(x_l, \theta\right):=D\left[q\left(y \mid x_l\right), p\left(y \mid x_l+r_{\mathrm{adv}}, \theta\right)\right] \\ \text { where } r_{\mathrm{adv}}:=\underset{r ; \mid \mid r \mid \mid \leq \epsilon}{\arg \max } D\left[q\left(y \mid x_l\right), p\left(y \mid x_l+r, \theta\right)\right] \end{array}\).
Notation
-
\(D\left[p, p^{\prime}\right]\) : non-neg function, measuring divergence between \(p\) & \(p^{\prime}\)
- ex) CE loss : \(D\left[p, p^{\prime}\right]=-\sum_i p_i \log p_i^{\prime}\)
-
\(q\left(y \mid x_l\right)\) : true distn of output label (unknown)
-
goal : approximate \(q\left(y \mid x_l\right)\) by a parametric model \(p\left(y \mid x_l, \theta\right)\) , which is robust against adversarial attack to \(x\).
-
( previous works, with labeled dataset ) approximate \(q\left(y \mid x_l\right)\) by one-hot vector \(h\left(y ; y_l\right)\)
\(\leftrightarrow\) our work : semi-supervised case
-
Approximation
\(r_{adv}\) : cannot obtain closed form
\(\rightarrow\) approximate with **linear approximation of D\(, w.r.t\)r$$
When norm is \(L_2\) …. \(r_{\mathrm{adv}} \approx \epsilon \frac{g}{ \mid \mid g \mid \mid _2}\),
-
where \(g=\nabla_{x_l} D\left[h\left(y ; y_l\right), p\left(y \mid x_l, \theta\right)\right]\)
( can be calculated during back-prop )
When norm is \(L_{\infty}\) …. \(r_{\mathrm{adv}} \approx \epsilon \operatorname{sign}(g)\)
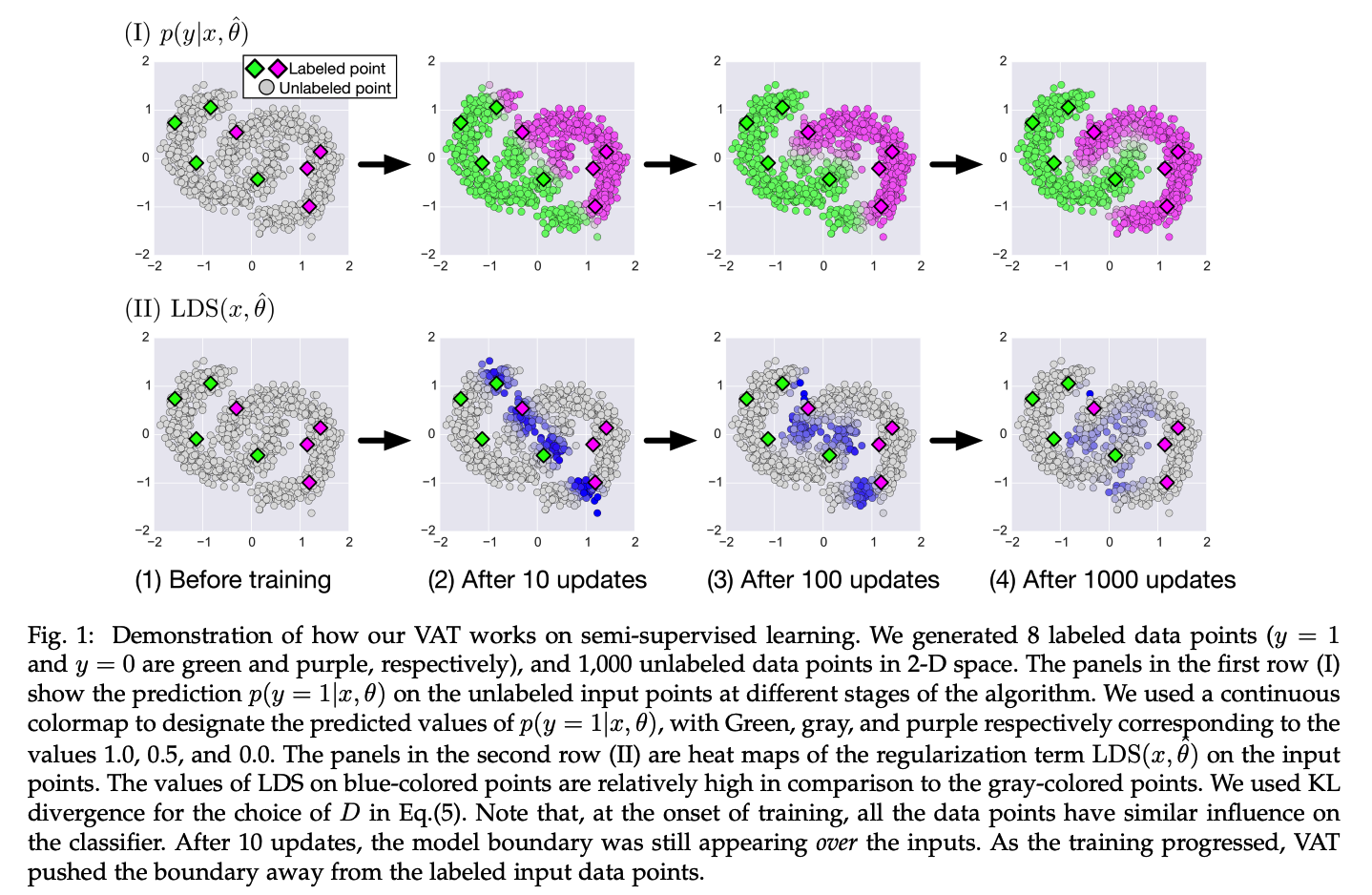
(2) Virtual Adversarial Training (VAT)
( Let \(x_*\) represent either \(x_l\) or \(x_{u l}\). )
\(\rightarrow\) \(\because\) applicable to both labeled & unlabeled data
Objective Function :
\(D\left[q\left(y \mid x_*\right), p\left(y \mid x_*+r_{\mathrm{qadv}}, \theta\right)\right]\),
- where \(r_{\mathrm{qadv}}:=\underset{r ; \mid \mid r \mid \mid \leq \epsilon}{\arg \max } D\left[q\left(y \mid x_*\right), p\left(y \mid x_*+r, \theta\right)\right]\)
But, have no info about \(q\left(y \mid x_{u l}\right)\)
\(\rightarrow\) replace \(q(y \mid x)\) with its current approximation, \(p(y \mid x, \theta)\)
Thus, use the current estimate \(p(y \mid x, \hat{\theta})\) instead of \(q(y \mid x)\).
New loss ( using virtual adversarial perturbation )
\(\begin{array}{r} \operatorname{LDS}\left(x_*, \theta\right):=D\left[p\left(y \mid x_*, \hat{\theta}\right), p\left(y \mid x_*+r_{\mathrm{vadv}}, \theta\right)\right] \\ r_{\mathrm{vadv}}:=\underset{r ; \mid \mid r \mid \mid _2 \leq \epsilon}{\arg \max } D\left[p\left(y \mid x_*, \hat{\theta}\right), p\left(y \mid x_*+r\right)\right] \end{array}\).
The regularization term we propose in this study is the average of \(\operatorname{LDS}\left(x_*, \theta\right)\) over all input data points
\(\rightarrow\) \(\mathcal{R}_{\mathrm{vadv}}\left(\mathcal{D}_l, \mathcal{D}_{u l}, \theta\right):=\frac{1}{N_l+N_{u l}} \sum_{x_* \in \mathcal{D}_l, \mathcal{D}_{u l}} \operatorname{LDS}\left(x_*, \theta\right)\).
Full loss function : \(\ell\left(\mathcal{D}_l, \theta\right)+\alpha \mathcal{R}_{\mathrm{vadv}}\left(\mathcal{D}_l, \mathcal{D}_{u l}, \theta\right)\)
- where \(\ell\left(\mathcal{D}_l, \theta\right)\) : NLL for labeled dataset