Complex Numbers for Audio Signal Processing
참고 : https://www.youtube.com/watch?v=fMqL5vckiU0&list=PL-wATfeyAMNrtbkCNsLcpoAyBBRJZVlnf
1. Why use complex number in audio?
To express both (1) frequency & (2) phase!
- complex numbers : \(c = a+ib\)
- where \(a,b \in \mathbb{R}\).
- \(a\) : REAL part
- \(ib\) : IMAGINARY part
Plotting complex numbers in …
(1) Cartesian coordinates
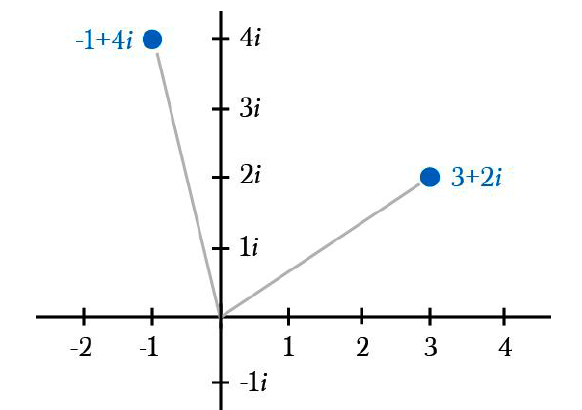
(2) Polar coordinates
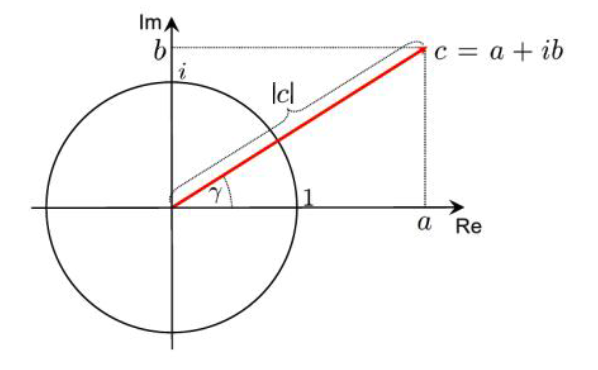
- express using \(c\) and \(\gamma\)
2. Polar Coordinates
\(\cos (\gamma)=\frac{a}{ \mid c \mid }\).
\(\rightarrow\) \(a= \mid c \mid \cdot \cos (\gamma)\)
\(\sin (\gamma)=\frac{b}{ \mid c \mid }\).
\(\rightarrow\) \(b= \mid c \mid \cdot \sin (\gamma)\)
\(\rightarrow\) \(c= \mid c \mid \cdot(\cos (\gamma)+i \sin (\gamma))\).
\(\text{tan}(\gamma) = \frac{\sin (\gamma)}{\cos (\gamma)}=\frac{b}{a}\).
\(\rightarrow\) \(\gamma=\arctan \left(\frac{b}{a}\right)\).
3. Eular Formula
(1) Euler formula
\(e^{i \gamma}=\cos (\gamma)+i \sin (\gamma)\).
(2) Euler identity
\(e^{i\pi} +1=0\).
\(\rightarrow\) \(e^{i\pi}=-1\).
(3) Polar coordinates 2.0
\(c= \mid c \mid \cdot(\cos (\gamma)+i \sin (\gamma))\).
\(e^{i \gamma}=\cos (\gamma)+i \sin (\gamma)\).
\(\rightarrow\) \(c= \mid c \mid e^{i\gamma}\).
- can express complex number \(c\) with
- (1) \(\mid c \mid\) : magnitude
- (2) \(\gamma\) : direction
Interpretation

\(\rightarrow\) why not use MAGNITUDE & PHASE as polar coordinates?
4. Fourier Transform using Complex Number
(1) Magnitude & Phase
Magnitude
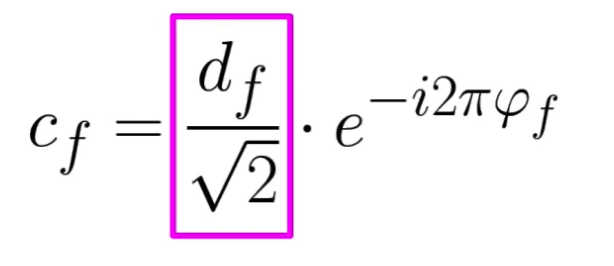
Phase
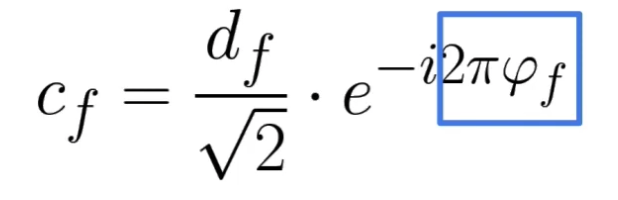
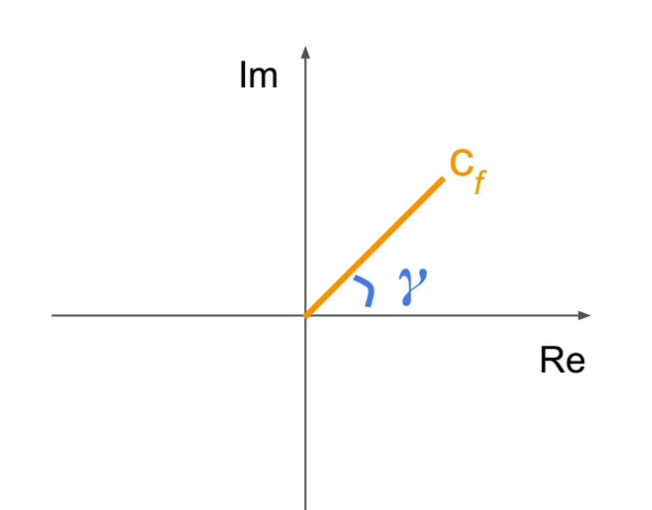
- meaning of \(-\) : rotate “clock-wise”
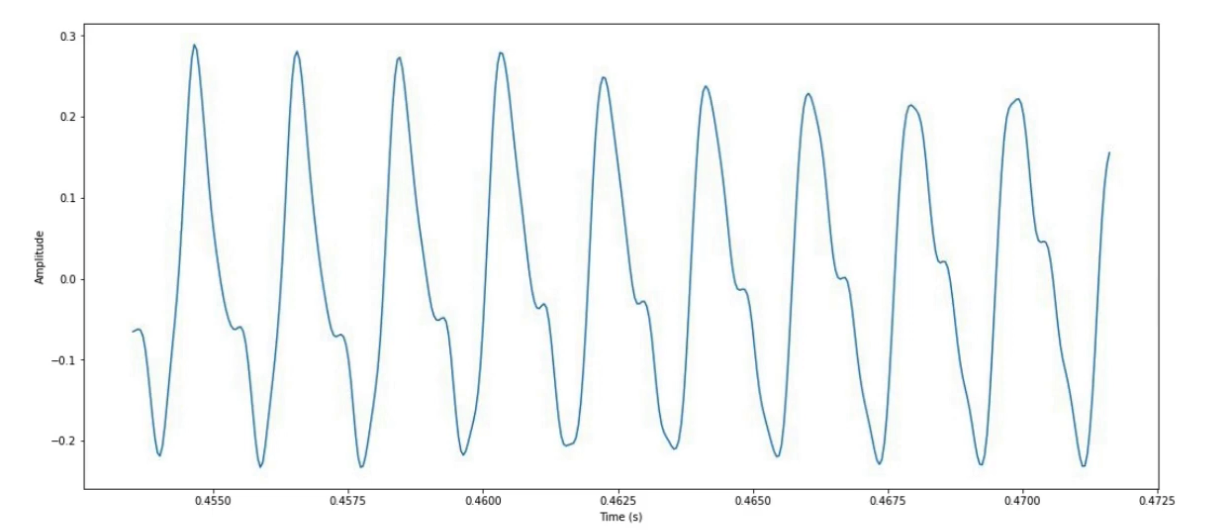
(2) Continuous audio signal
\(g(t) \quad g: \mathbb{R} \rightarrow \mathbb{R}\).
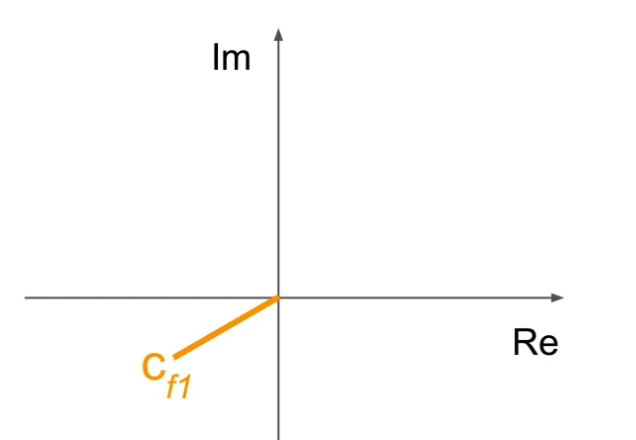
(3) COMPLEX Fourier Transform
\(\hat{g}(f)=c_f\).
- \(\hat{g}: \mathbb{R} \rightarrow \mathbb{C}\).
Mapping into a complex space!
Mathematical Expression
\(\hat{g}(f)=\int g(t) \cdot e^{-i 2 \pi f t} d t\).
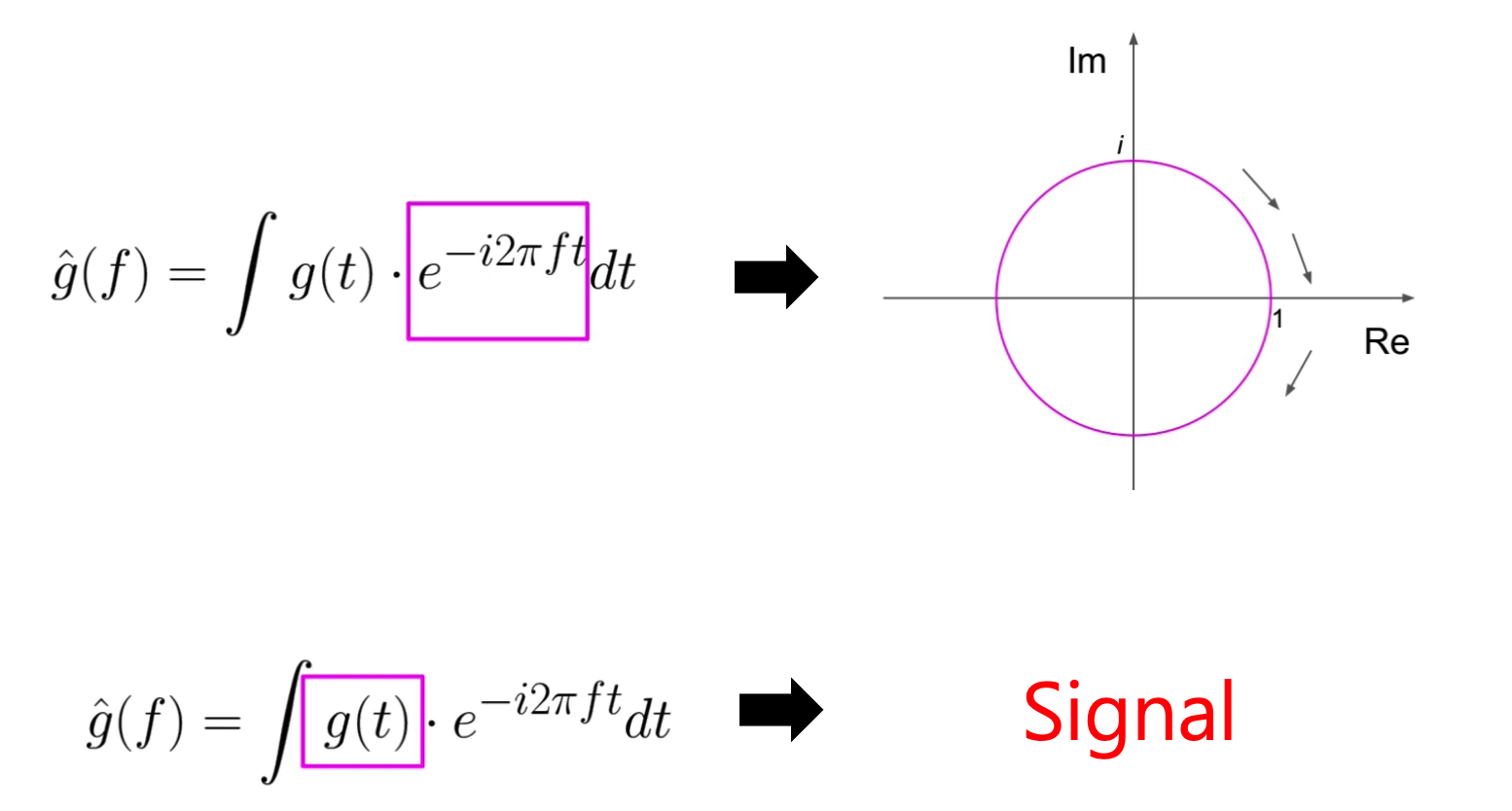
(4) Complex Fourier Transform coefficients
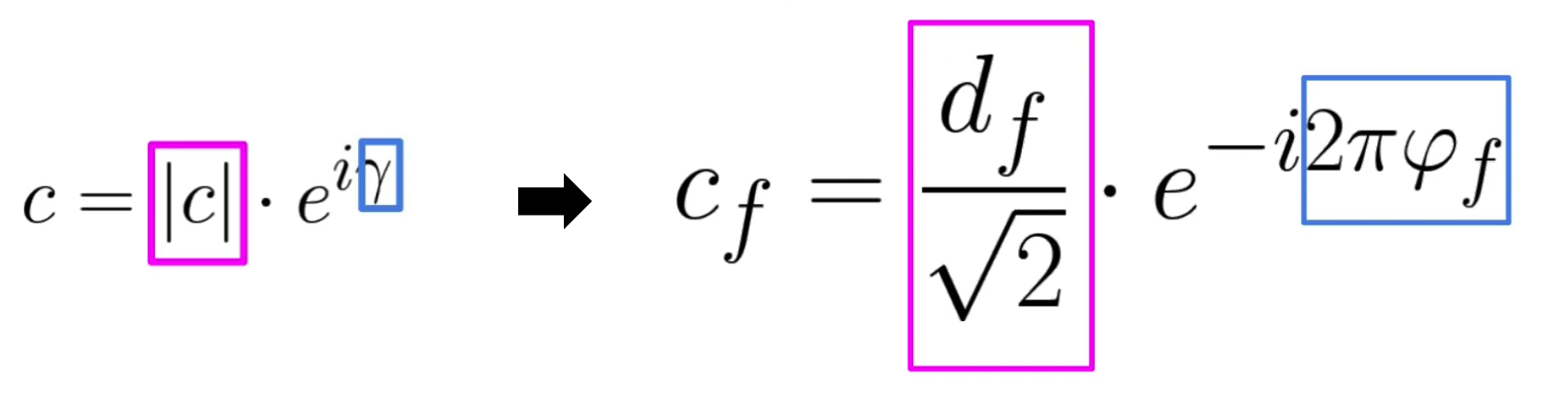
(5) Magnitude & Phase
\(c_f=\frac{d_f}{\sqrt{2}} \cdot e^{-i 2 \pi \varphi_f}\).
a) Magnitude
ABSOLUTE value of \(\hat{g}(f)\)
= REAL part of \(c_f\)
= \(d_f=\sqrt{2} \cdot \mid \hat{g}(f) \mid\).
b) Phase
IMAGINARY value of \(\hat{g}(f)\)
= \(\varphi_f=-\frac{\gamma_f}{2 \pi}\).
5. Fourier & Inverse Fourier Transform
\(\begin{gathered} \hat{g}(f)=\int g(t) \cdot e^{-i 2 \pi f t} d t \\ g(t)=\int c_f \cdot e^{i 2 \pi f t} d f \end{gathered}\).
