The Rise of Diffusion Models in Time-Series Forecasting
Contents
- Abstract
- Introduction
- Diffusion Model
- DDPM
- Score-based generative modeling via SDE
- Conditional Diffusion Models
- Diffusion Models for TS Modeling
0. Abstract
-
Diffusion models for TS forecasting
-
11 specific TS implementations
1. Introduction
Diffusion models in TS forecasting
-
[Section 1.1] TS forecasting & How to evaluate
-
[Section 2] Intrinsic works of diffusion & How to condition
-
[Section 3] Diffusion-based TS forecasting papers
(1) Problem Definition
-
Observations: \(o b s=\{t \in \mathbb{Z} \mid-H<t \leq 0\}\) \(\rightarrow\) \(X_{\text {obs }} \in \mathbb{R}^{d \times H}\)
-
Targets: \(\operatorname{tar}=\{t \in \mathbb{Z} \mid 0<t \leq F\}\). \(\rightarrow\) \(X_{\text {tar }} \in \mathbb{R}^{d \times F}\)
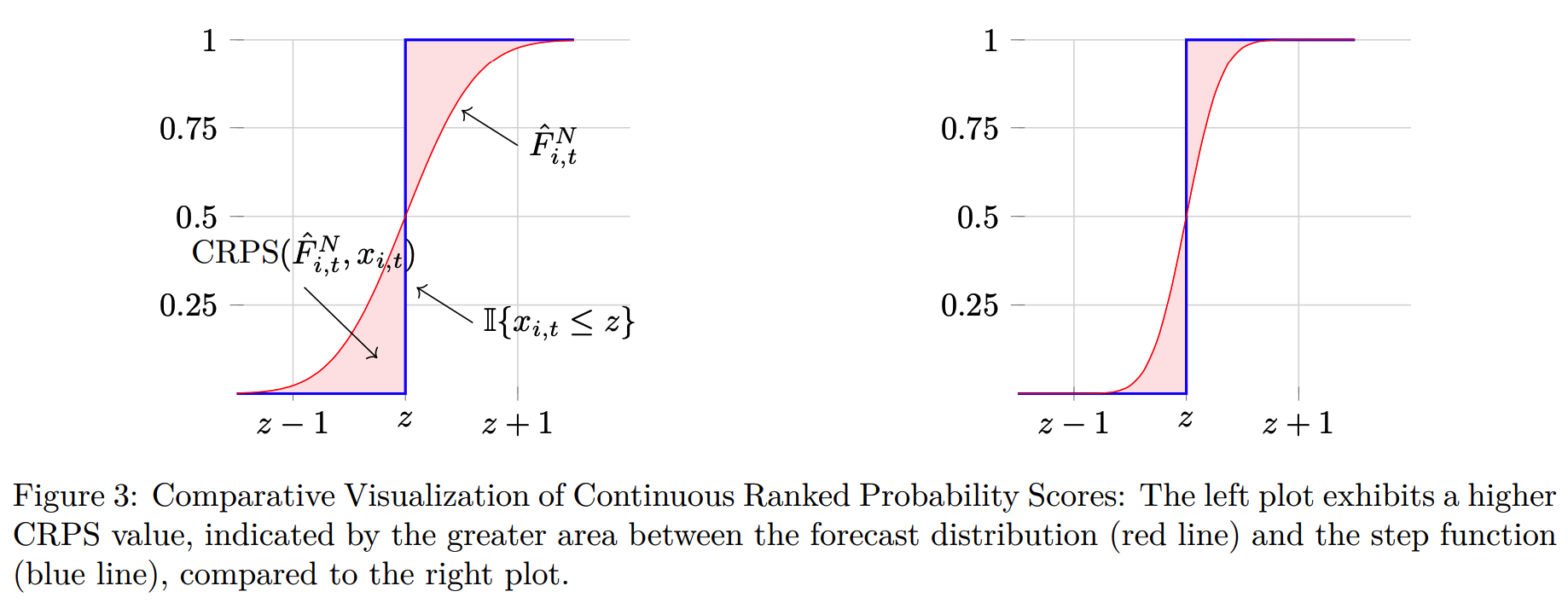
(2) Continuous Ranked Probability Score (CRPS)
-
Takes into account the uncertainty of the prediction
-
For probabilistic forecasting …. measures the compatibility of CDF \(F\) with an observation \(X_{t a r}\).
-
CDF \(F\) is not available analytically
\(\rightarrow\) Estimate it through a set of \(N\) forecast samples \(\hat{X}_{\text {tar }}^N\)
\(\rightarrow\) Gathered by sampling the probabilistic model \(N\) times.
-
Calculated for of a single feature at a single timestamp
Empirical CDF \(\hat{F}_N(z)\)
-
given a point \(z\) from these predictions.
-
\(\hat{F}_{i, t}^N(z)=\frac{1}{N} \sum_{n=1}^N \mathbb{I}\left\{\hat{x}_{i, t}^n \leq z\right\}\).
CRPS for the empirical \(\operatorname{CDF} \hat{F}_N\) & \(X_{t a r}\)
- \(\operatorname{CRPS}\left(\hat{F}_{i, t}^N, x_{i, t}\right)=\int_{\mathbb{R}}\left(\hat{F}_{i, t}^N(z)-\mathbb{I}\left\{x_{i, t} \leq z\right\}\right)^2 d z\).
CRPS focuses on a single feature at a specific timestamp
\(\rightarrow\) Howabout MTS with multiple timestamps ??
\(\rightarrow\) Some normalization and averaging ought to be done!
-
(1) Normalized Average CRPS
-
(2) CRPS-sum
(1) Normalized Average CRPS
- \(\operatorname{NACRPS}\left(\hat{F}^N, X_{\text {tar }}\right)=\frac{\sum_{i, t} \operatorname{CRPS}\left(\hat{F}_{i, t}^N, x_{i, t}\right)}{\sum_{i, t} \mid x_{i, t} \mid }\).
(2) CRPS-sum
-
CRPS for the distribution F for the sum of all \(d\) features
-
\(\operatorname{CRPS}_{\text {sum }}\left(\hat{F}^N, X_{\text {tar }}\right)=\frac{\sum_t \operatorname{CRPS}\left(\hat{F}_{i, t}^N, \sum_i x_i\right)}{\sum_{i, t} \mid x_{i, t} \mid }\).
2. Diffusion Model
(1) DDPM
Noise Prediction
- \(\mathcal{L}_{\epsilon_\theta}=\mathbb{E}_{k, x^0, \epsilon}\left[ \mid \mid \epsilon-\epsilon_\theta\left(x^k, k\right) \mid \mid ^2\right]\).
- where \(\mu_\epsilon\left(\epsilon_\theta\right)=\frac{1}{\sqrt{1-\beta_k}}\left(x^k-\frac{\beta_k}{\sqrt{1-\alpha_k}} \epsilon_\theta\left(x^k, k\right)\right)\)
Data prediction
- \(\mathcal{L}_{x_\theta}=\mathbb{E}_{k, x^0, \epsilon}\left[ \mid \mid x^0-x_\theta\left(x^k, k\right) \mid \mid ^2\right]\).
- where \(\mu_x\left(x_\theta\right)=\frac{\sqrt{1-\beta_k}\left(1-\alpha_{k-1}\right)}{1-\alpha_k} x^k+\frac{\sqrt{\alpha_{k-1}} \beta_k}{1-\alpha_k} x_\theta\left(x^k, k\right)\).

(2) Score-based generative modeling via SDE
Forward difffusion process
- \(\mathrm{d} x=f(x, k) \mathrm{d} k+g(k) \mathrm{d} \mathbf{w}v\).
Reverse denoising process
- \(\mathrm{d} x=\left[f(x, k)-g(k)^2 \nabla_x \log p_k(x)\right] \mathrm{d} k+g(k) d \overline{\mathbf{w}}\).
Score objective function
- \(\mathcal{L}_{s_\theta}=\mathbb{E}_{k, x(0), x(k)}\left[ \mid \mid \nabla_{x(k)} \log p_{0 k}(x(k) \mid x(0))-s_\theta(x(k), k) \mid \mid ^2\right]\).
- with a time dependent score-based model \(s_\theta(x, k)\) using

DDPM = VP SDE
\(\mathrm{d} x=-\frac{1}{2} \beta(k) x \mathrm{~d} k+\sqrt{\beta(k)} \mathrm{d} \mathbf{w}\).
Sub-VP SDE
\(\mathrm{d} x=-\frac{1}{2} \beta(k) x \mathrm{~d} k+\sqrt{\beta(k)\left(1-\mathrm{e}^{-2 \int_0^k \beta(s) d s}\right)} \mathrm{d} \mathbf{w}\).
SDE \(\rightarrow\) ODE
From each SDE, one can derive an ODE with the same marginal distributions = Probability Flow ODE (PF-ODE)
\(\mathrm{d} x=\left[f(x, k)-\frac{1}{2} g(k)^2 \nabla_x \log p_k(x)\right] \mathrm{d} k\).
(3) Conditional Diffusion Models
a) Conditional Denoising Model
With additional input \(c\) … altering the backward denoising step i
- \(p_\theta\left(x^{0: K} \mid \mathbf{c}\right)=p\left(x^K\right) \prod_{k=1}^K p_\theta\left(x^{k-1} \mid x^k, \mathbf{c}\right) \text { with } p_\theta\left(x^{k-1} \mid x^k, \mathbf{c}\right)=\mathcal{N}\left(x^{k-1} ; \mu_\theta\left(x^k, k \mid \mathbf{c}\right), \sigma_k^2 \mathbf{I}\right)\).
Noise & Data prediction models
- \(\mu_\epsilon\left(\epsilon_\theta, \mathbf{c}\right)=\frac{1}{\sqrt{1-\beta_k}}\left(x^k-\frac{\beta_k}{\sqrt{1-\alpha_k}} \epsilon_\theta\left(x^k, k \mid \mathbf{c}\right)\right)\).
- \(\mu_x\left(x_\theta, \mathbf{c}\right)=\frac{\sqrt{1-\beta_k}\left(1-\alpha_{k-1}\right)}{1-\alpha_k} x^k+\frac{\sqrt{\alpha_{k-1}} \beta_k}{1-\alpha_k} x_\theta\left(x_k, k \mid \mathbf{c}\right)\).
Reverse-time SDE
- \(d x=\left[f(x, k)=g(k)^2 \nabla_x \log p_k(x \mid \mathbf{c})\right] d k+g(k) d \bar{w}\).
Objective function
- \(\mathcal{L}_k=\mathbb{E}_{k, x(0), x(k)}\left[ \mid \mid \nabla_{x(k)} \log p_{0 k}(x(k) \mid x(0))-s_\theta(x(k), k \mid \mathbf{c}) \mid \mid ^2\right]\).

b) Diffusion Guidance
With Bayes’ rule..
- \(\nabla_{x^k} \log p\left(x^k \mid \mathbf{c}\right)=\nabla_{x^k} \log p\left(\mathbf{c} \mid x^k\right)+\nabla_{x^k} \log p\left(x^k\right)\).
Reverse diffusion process:
- \(p_\theta\left(x^{k-1} \mid x^k, \mathbf{c}\right)=\mathcal{N}\left(x^{k-1} ; \mu_\theta\left(x^k, k\right), \sigma_k^2 \mathbf{I}\right)+ s \sigma_k^2 \nabla_{x^k} \log p\left(\mathbf{c} \mid x^k\right)\).
\(s \sigma_k^2 \nabla_{x^k} \log p\left(\mathbf{c} \mid x^k\right)\).
- guidance term
- with…
- (1) w/ auxiliary model
- (2) w/o auxiliary model
Can also be applied to the continuous diffusion models
- \(\mathrm{d} x=\left\{f(x, k)-g(k)^2\left[\nabla_x \log p_k(x)+\nabla_x \log p_k(\mathbf{c} \mid x)\right]\right\} \mathrm{d} k+g(k) d \bar{w}\).

3. Diffusion Models for TS Modeling
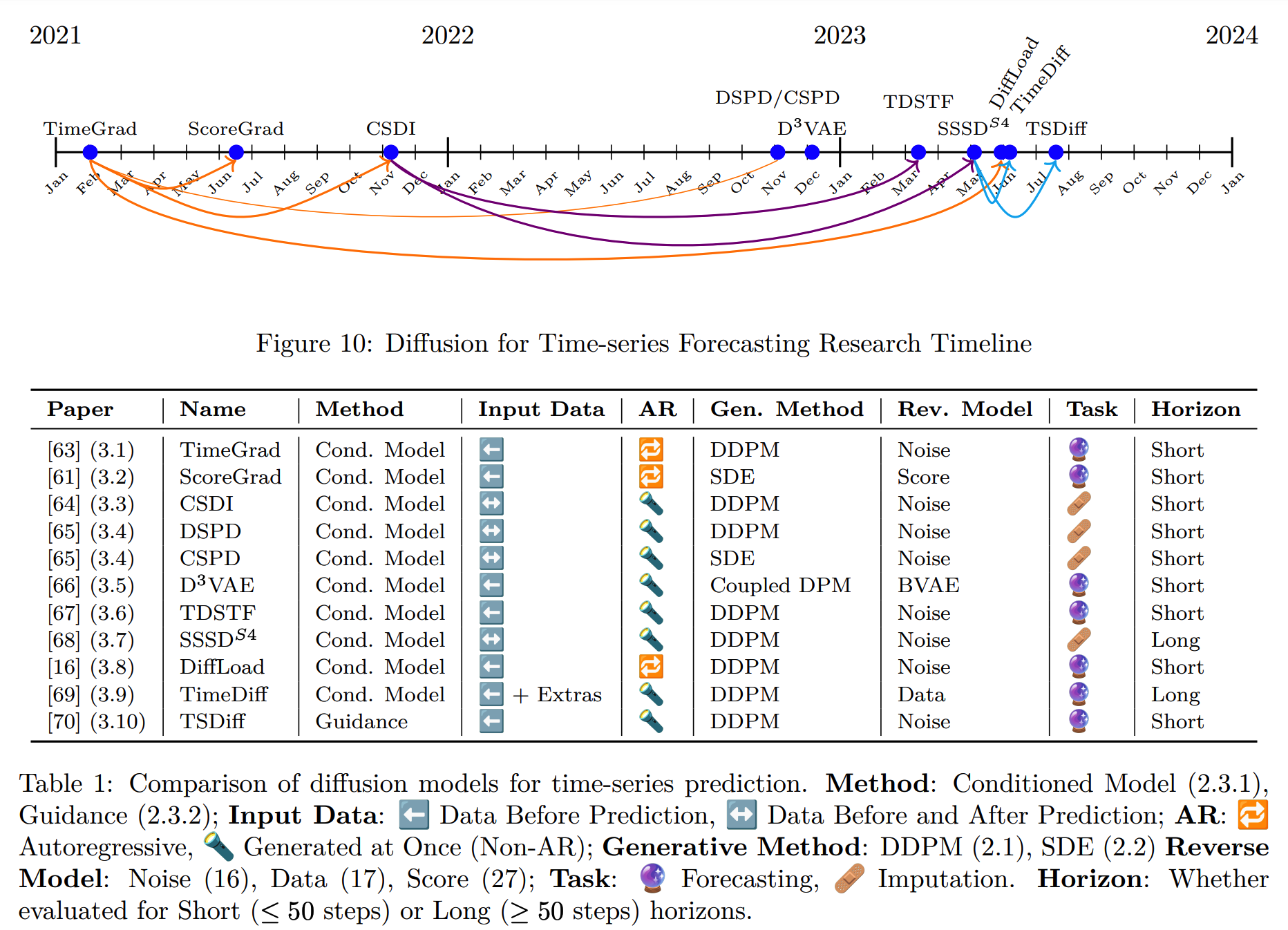
Dataset summary
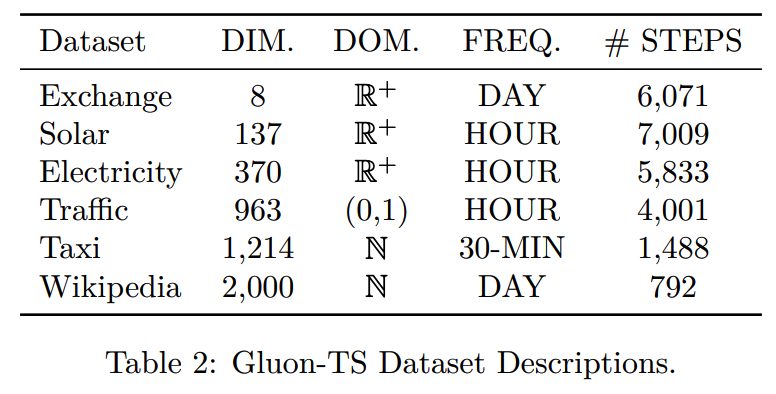
(1) TimeGrad (2021)
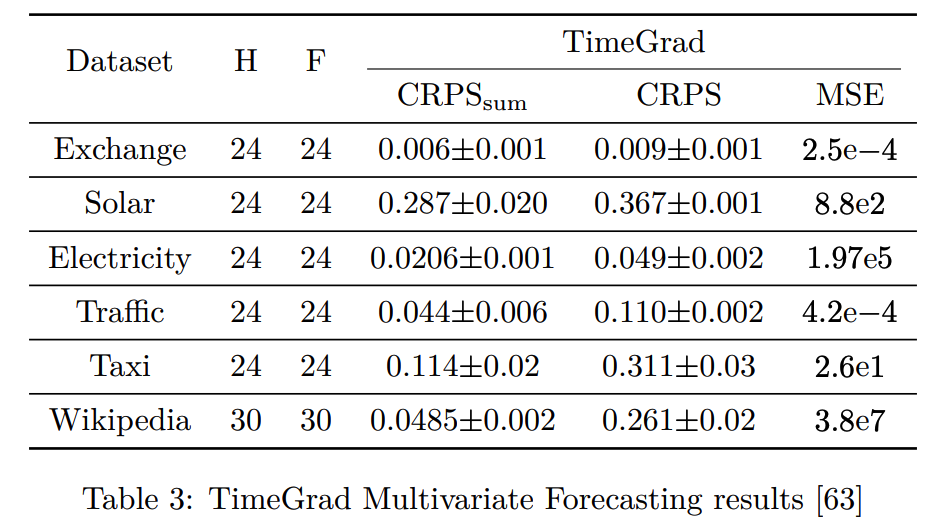
(2) ScoreGrad (2021)
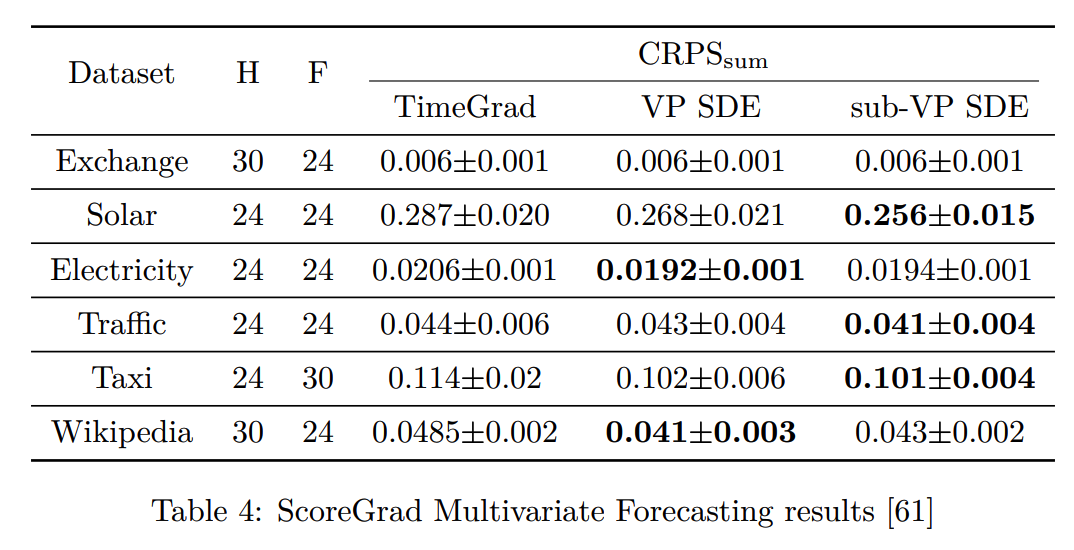
(3) CSDI (2021)
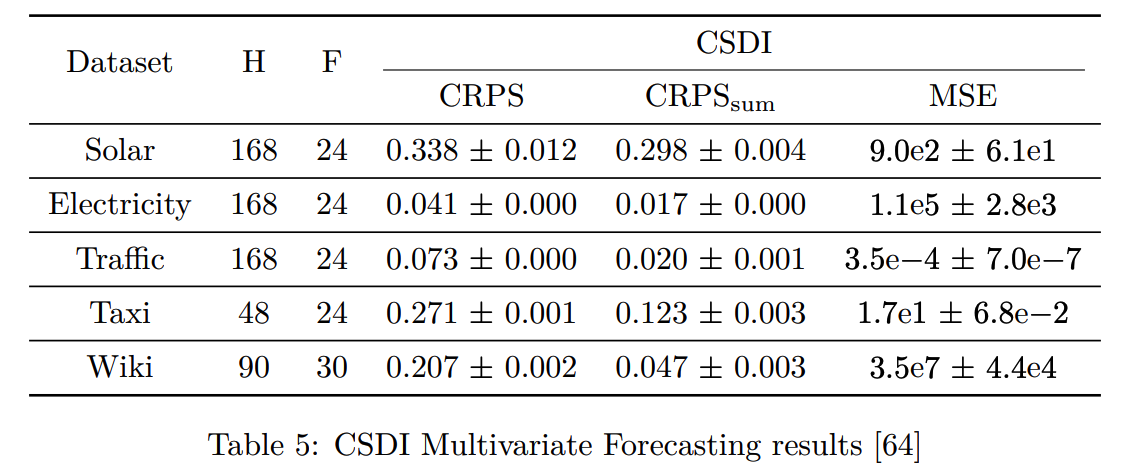
(4) DSPD & CSPD (2022)
DSPD = Discrete Stochastic Process Diffusion
CSPD = Continuous ~
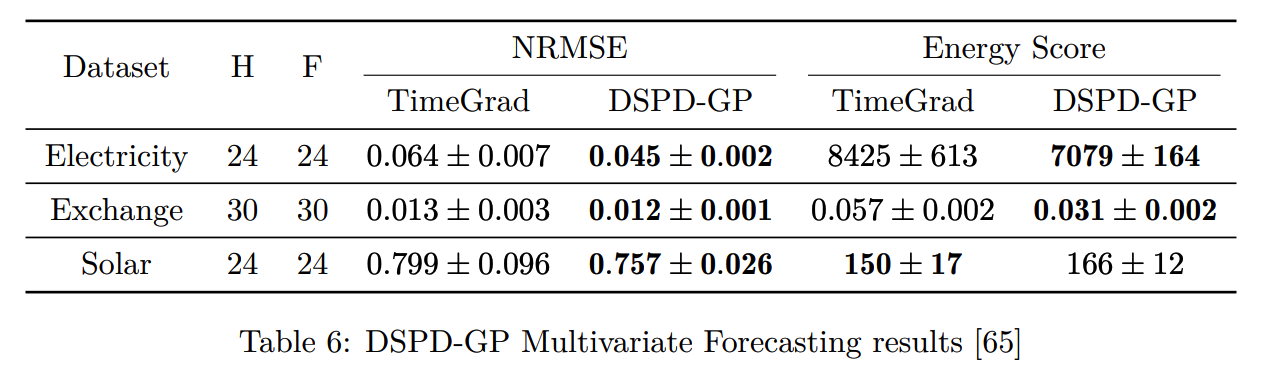
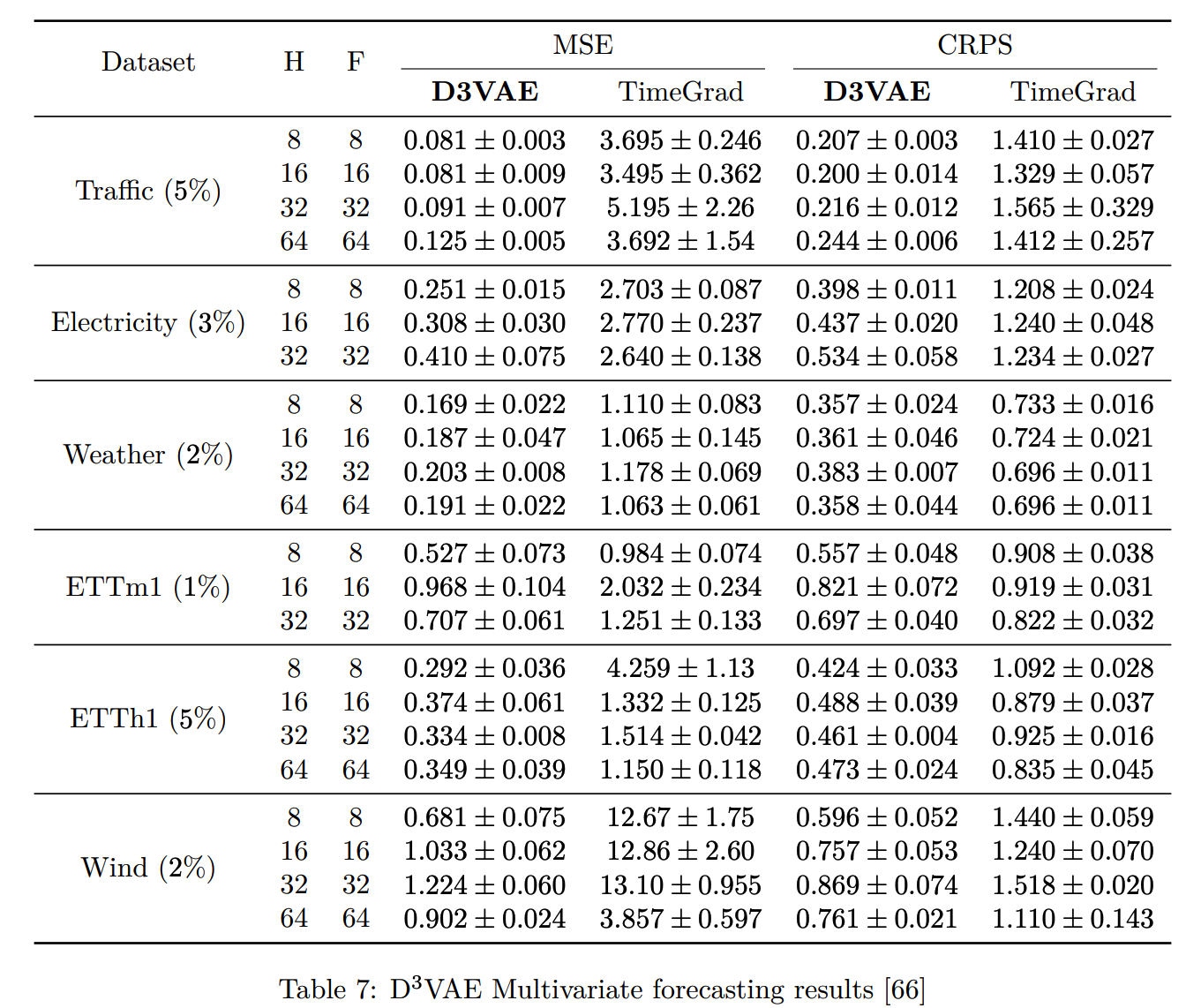
(5) D\(^3\)VAE (2022)
(6) TDSTF (2023)

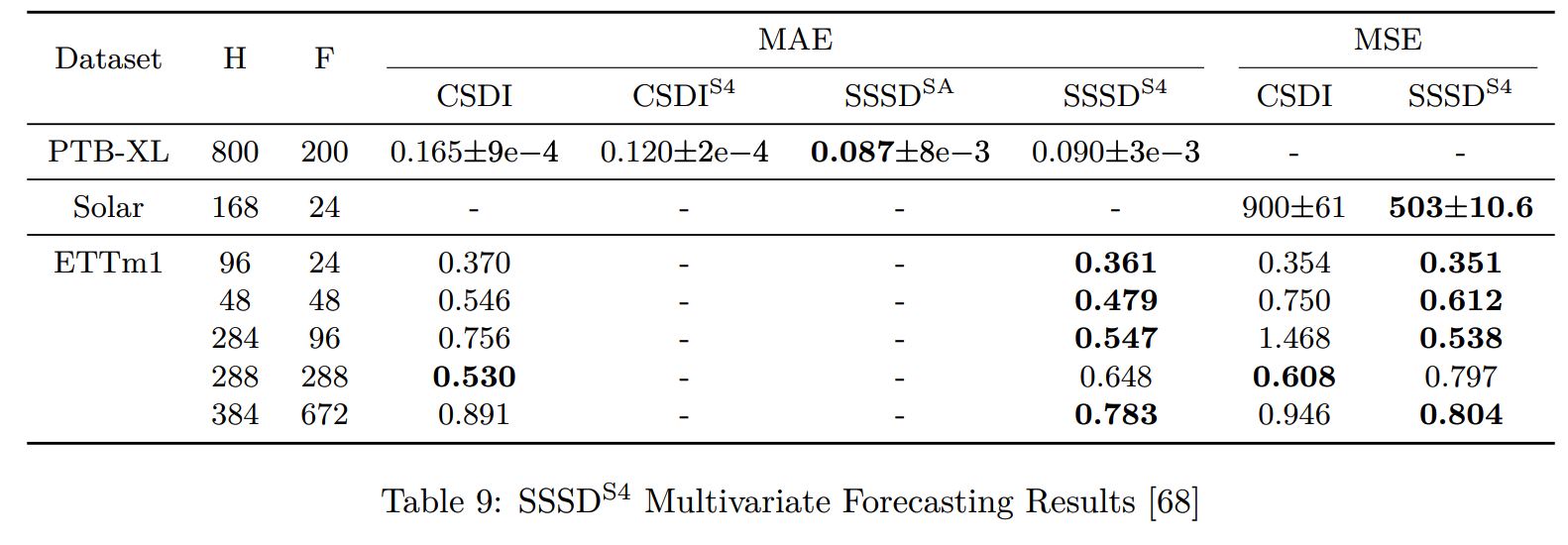
(7) SSSD\(^{S4}\) (2023)
(8) DiffLoad (2023)

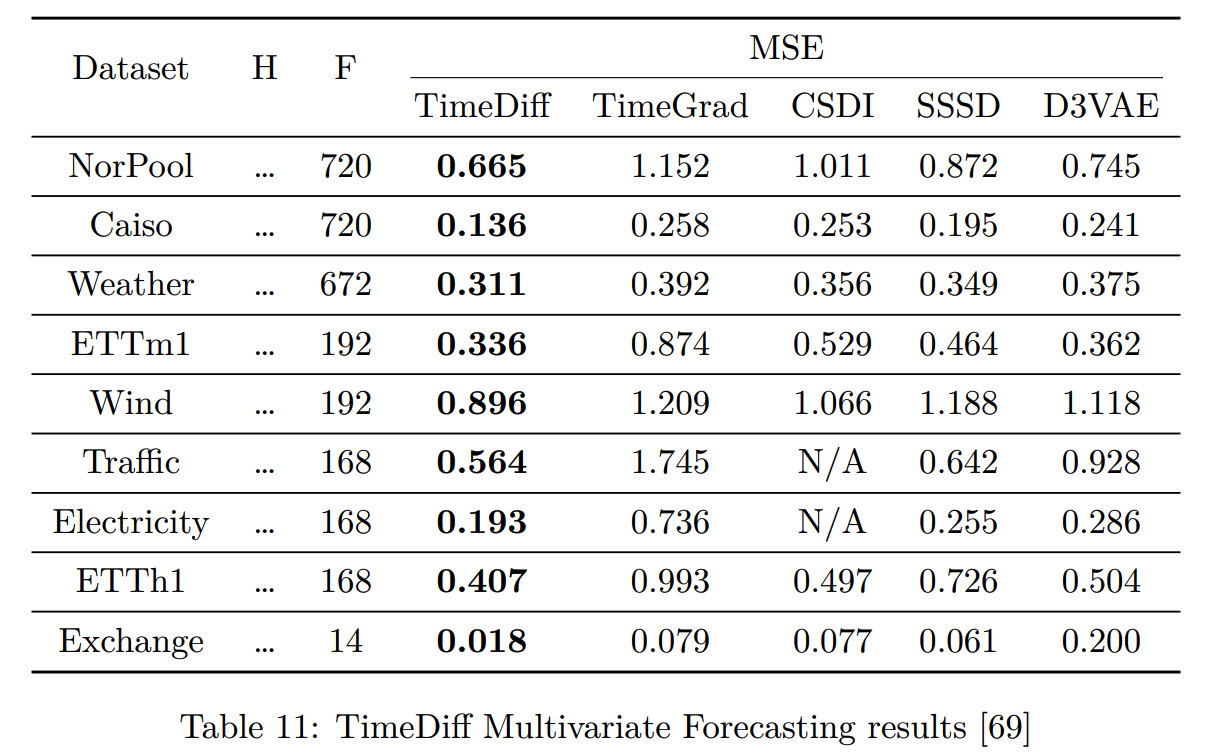
(9) TimeDiff (2023)
(10) TSDiff (2023)