(paper) Pyraformer ; Low-Complexity Pyramidal Attention for Long-Rang TS modeling and forecasting

Pyraformer : Low-Complexity Pyramidal Attention for Long-Rang TS modeling and forecasting (2022)

Contents

1. Abstract
2. Introduction
3. Hierarchical Transformers
4. Method
   1. PAM ( Pyramidal Attention Module )
   2. CSCM ( Coarser-Scale Construction Module )
   3. Prediction Module

0. Abstract

Pyraformer

• explore the MULTI-resolution representation of TS
• introduce PAM (pyramidal attention module)
  • Inter-scale tree structure : sumamrise features at different resolution
  • Intra-scale neighboring connections : model the temporal dependencies of different ranges
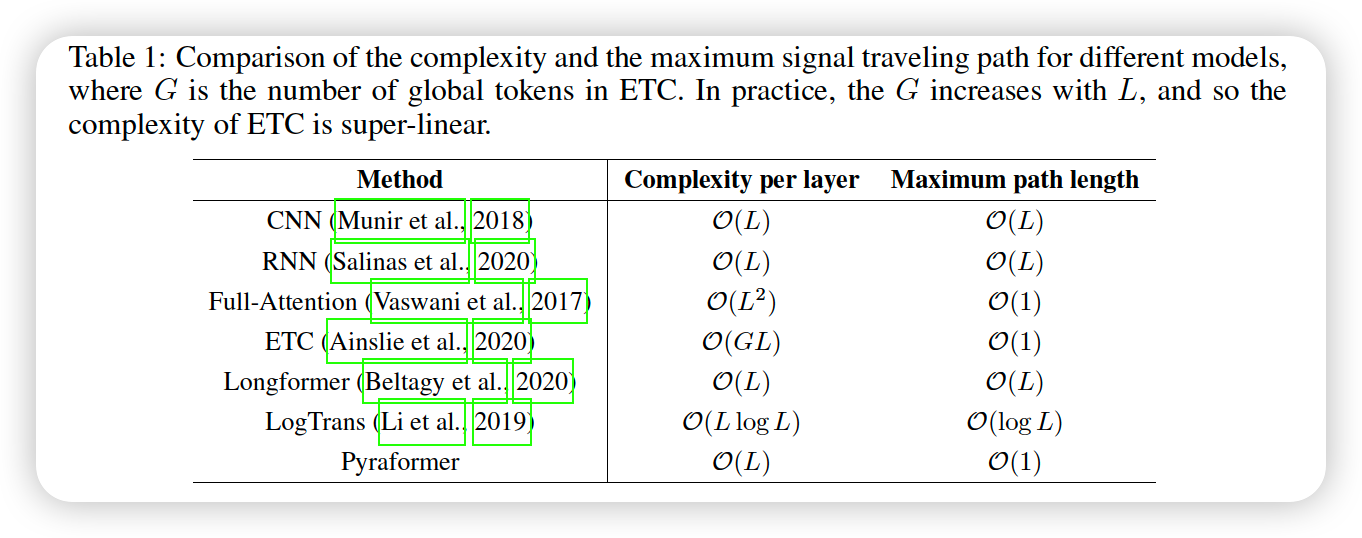
• complexity : \(O(1)\)

1. Introduction

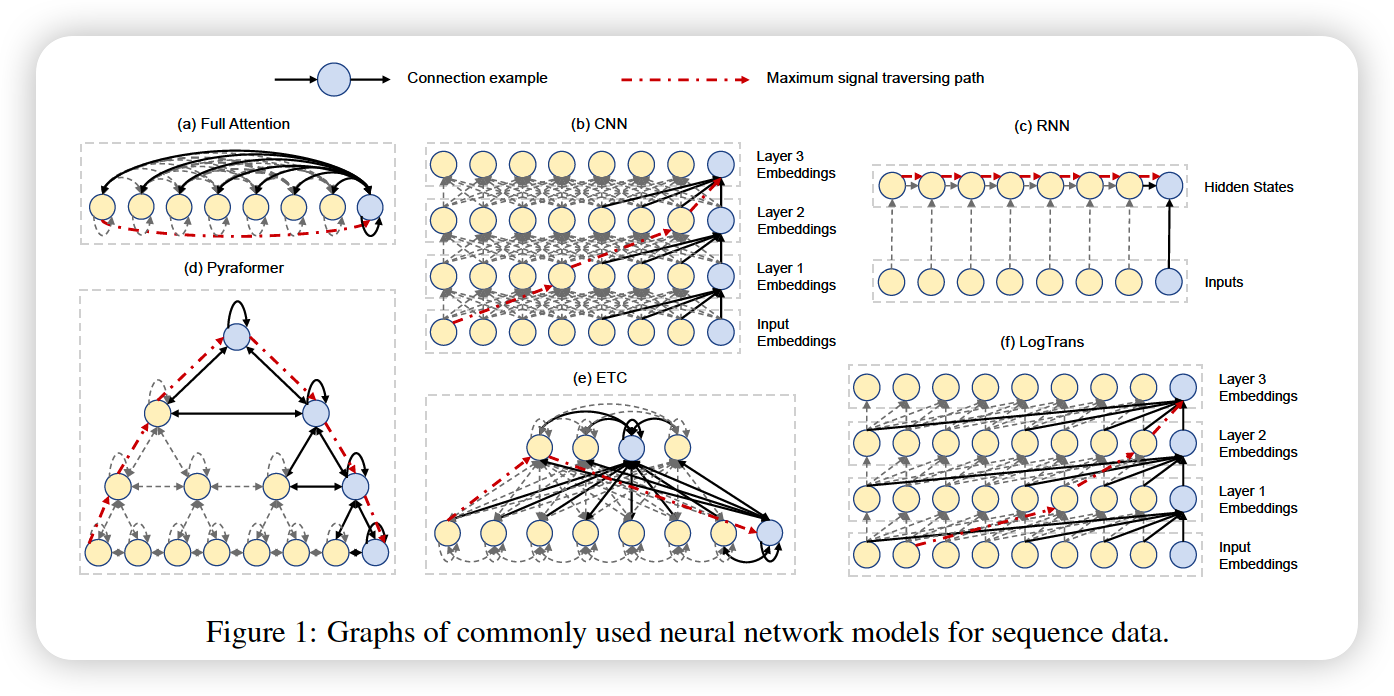
RNN & CNN

• low time complexity : linear in temrs of TS length \(L\)
• maximum length of signal traversing path : \(O(L)\)

\(\rightarrow\) difficult to learn dependencies between distant positions

Transformer

• shortens the maximum path : \(O(1)\)
• high time complexity : \(O(L^2)\)

\(\rightarrow\) difficult in very long TS

Compromise between two :

• LongFormer (2020)
• Reformer (2019)
• Informer (2021)

\(\rightarrow\) but, few of them achive a maximum path length less that \(O(L)\)

Pyraformer

( Pyramidal Attention based Transformer )

(1) Inter scale

• multi-resolution representation

(2) Intra scale

• captures the temporal dependencies at each resolution,

  by connecting neighboring nodes together

Summary

• maximum path length : \(O(1)\)
• time & space complexity : \(O(L)\)

2. Hierarchical Transformers

HIBERT (2018)

• uses a Sent Encoder to extract features of a sentences

• forms the EOS tokens of sentences in the document, as a new sequence

  & input into Doc Encoder

• limited to NLP

Multi-scale Transformer (2020)

• using both top-down & bottom-up network

• help reduce time & memory cost of original Transformer

• still sfufers from quadratic complexity

BP-Transformer (2019)

• recusrively partitions the entire input sentence into 2 ,

  until a partition only contains a single token

BP-Transformer vs Pyraformer

• BP-Transformer
  • initializes the nodes at coarser scale with 0
  • Higher complexity : \(O(L\log L)\)
• Pyraformer
  • introduces the coarser-scale nodes using a construction module

3. Method

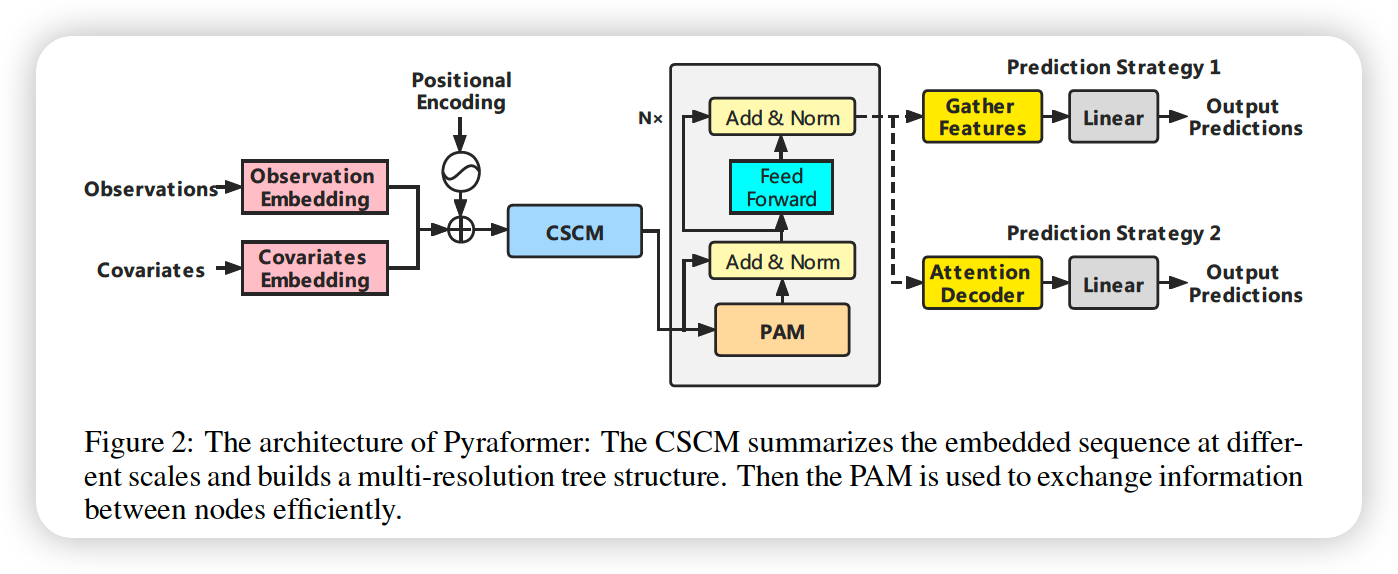
Notation

• predict future \(M\) steps : \(z_{t+1: t+M}\)
• given ..
  • (1) previous \(L\) steps : \(\boldsymbol{z}_{t-L+1: t}\)
  • (2) covariates : \(\boldsymbol{x}_{t-L+1: t+M}\)

Process

• step 1) embed three things & add them
  • (1) data
  • (2) covariate
  • (3) position
• step 2) construct a multi-resolution \(C\)-ary tree
  • Using CSCM ( Coarser-Scale Construction Module )
• step 3) use PAM, by passing messages using attention in pyramidal graph
• step 4) different network structures to output final predictions

3-1. PAM ( Pyramidal Attention Module )

• Inter-scale & intra scale
• easier to capture long-range dependencies
• multi resolution
  • finest scale : ex) hourly
  • coarser scale : ex) daily, weekly
• opposed to full-attention, pyramidal-attention only pays attention to a linited set of keys

3-2. CSCM ( Coarser-Scale Construction Module )

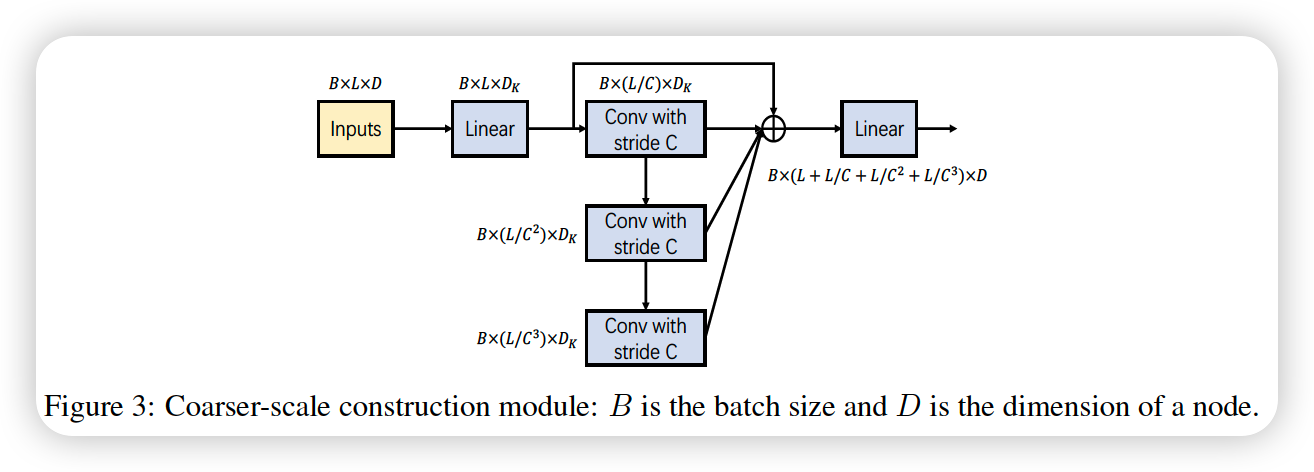
to facilitate the subsequent PAM to exchange information between nodes

• several convolution layers with kernel size \(C\) & stride \(C\)

Concatenate these fine-to-coarse sequence before inputting them to PAM

3-3. Prediction Module

a) single-step forecasting

• add an end token ( \(z_{t+1}=0\) )

• after the sequence is encoded by PAM,

  gather the features given by last nodes at all scales in pyramidal graph

  concatenate them!

• pass them to FC layer

b) multi-step forecasting

b-1)

• same as a)
• just map last nodes (at all scales) to \(M\) future time steps

b-2)

• resort to the decoder with 2 full attention layers

• replace the observations at the future \(M\) time steps with 0,

  embed them,

  take 2 attention layers ( refer to the Figure )