Multivariate 1. 선형확률 과정 ( General Linear Process ) (1)
현실 : 종속변수 & 독립변수는 상호 작용을 한다
( 어떤걸 \(X\)로, 어떤걸 \(Y\)로 설정할지는 관심에 따라! )
Example) ‘소득’ & ‘지출’ 2개의 종속 변수
( 과거의 1시점까지 고려 )
\(\begin{align*} \text{Equation of VAR(1)} && Y_{[t]} &= A Y_{[t-1]} + \epsilon_{[t]} \\ \text{where} && Y_{[t]} &= \begin{bmatrix} Y_{1t} \\ Y_{2t} \end{bmatrix}, A = \begin{bmatrix} \phi_{11} \phi_{12} \\ \phi_{21} \phi_{22} \end{bmatrix}, Y_{[t-1]} = \begin{bmatrix} Y_{1t-1} \\ Y_{2t-1} \end{bmatrix}, \\ && \epsilon_{[t]} &= \begin{bmatrix} e_{1t} \\ e_{2t} \end{bmatrix} \sim N(0, \textstyle \sum_{\epsilon_{[t]}}) \\ \text{Each Equation of VAR(1)} && Y_{1t} &= \phi_{11} Y_{1t-1} + \phi_{12} Y_{2t-1} + e_{1t} \\ && Y_{2t} &= \phi_{21} Y_{1t-1} + \phi_{22} Y_{2t-1} + e_{2t} \\ \end{align*}\).
1. 벡터자기회귀 모형(VAR, Vector Autoregressive Model)
(1) VAR(1)
- 변수는 총 \(k\)개 있다고 가정
- ex) 국가A,국가B,…국가K의 GDP
where
\[\begin{aligned}Y_{[t]} = \begin{bmatrix} Y_{1t} \\ Y_{2t} \\ \vdots \\ Y_{kt} \end{bmatrix}, A_1 = \begin{bmatrix} \phi_{11}^1 \phi_{12}^1 \cdots \phi_{1k}^1 \\ \phi_{21}^1 \phi_{22}^1 \cdots \phi_{2k}^1 \\ \vdots \\ \phi_{k1}^1 \phi_{k2}^1 \cdots \phi_{kk}^1 \end{bmatrix}, Y_{[t-1]} = \begin{bmatrix} Y_{1t-1} \\ Y_{2t-1} \\ \vdots \\ Y_{kt-1} \end{bmatrix}, \epsilon_{[t]} = \begin{bmatrix} e_{1t} \\ e_{2t} \\ \vdots \\ e_{kt} \end{bmatrix} \sim N(0, \textstyle \sum_{\epsilon_{[t]}})\end{aligned}\](2) VAR(2)
\(Y_{[t]} = A_1 Y_{[t-1]} + A_2 Y_{[t-2]} + e_t\).
\(Y_{[t]} = \begin{bmatrix} Y_{1t} \\ Y_{2t} \\ \vdots \\ Y_{kt} \end{bmatrix}, Y_{[t-1]} = \begin{bmatrix} Y_{1t-1} \\ Y_{2t-1} \\ \vdots \\ Y_{kt-1} \end{bmatrix}, Y_{[t-2]} = \begin{bmatrix} Y_{1t-2} \\ Y_{2t-2} \\ \vdots \\ Y_{kt-2} \end{bmatrix} \\ A_1 = \begin{bmatrix} \phi_{11}^1 \phi_{12}^1 \cdots \phi_{1k}^1 \\ \phi_{21}^1 \phi_{22}^1 \cdots \phi_{2k}^1 \\ \vdots \\ \phi_{k1}^1 \phi_{k2}^1 \cdots \phi_{kk}^1 \end{bmatrix} A_2 = \begin{bmatrix} \phi_{11}^2 \phi_{12}^2 \cdots \phi_{1k}^2 \\ \phi_{21}^2 \phi_{22}^2 \cdots \phi_{2k}^2 \\ \vdots \\ \phi_{k1}^2 \phi_{k2}^2 \cdots \phi_{kk}^2 \end{bmatrix}, \epsilon_{[t]} = \begin{bmatrix} e_{1t} \\ e_{2t} \\ \vdots \\ e_{kt} \end{bmatrix} \sim N(0, \textstyle \sum_{\epsilon_{[t]}})\).
(3) VAR(p)
\[\begin{align*} &Y_{[t]} = A_1 Y_{[t-1]} + A_2 Y_{[t-2]} + \cdots + A_p Y_{[t-p]} + \epsilon_{[t]} \\\\ &\text{Mean} \mu_{[t]} = \text{E}(Y_{[t]}) = \begin{bmatrix} \text{E}(Y_{1t}) \\ \text{E}(Y_{2t}) \\ \vdots \\ \text{E}(Y_{kt}) \end{bmatrix} = \begin{bmatrix} \mu_{1} \\ \mu_{2}\\ \vdots \\ \mu_{k} \end{bmatrix} \\\\ &\text{Covariance } \Gamma(l) = \text{E}[(Y_{[t]} − \mu_{[t]})(Y_{[t]} − \mu_{[t]})^T ] \\ &= \begin{bmatrix} \text{E}[(Y_{1t} − \mu_1)^2] & \text{E}[(Y_{1t} − \mu_1)(Y_{2t} − \mu_2)] & \cdots & \text{E}[(Y_{1t} − \mu_1)(Y_{kt} − \mu_k)] \\ \text{E}[(Y_{2t} − \mu_2)(Y_{1t} − \mu_1)] & \text{E}[(Y_{2t} − \mu_2)^2] & \cdots & \text{E}[(Y_{2t} − \mu_2)(Y_{kt} − \mu_k)] \\ \vdots & \vdots & \ddots & \vdots \\ \text{E}[(Y_{kt} − \mu_k)(Y_{1t} − \mu_1)]& \text{E}[(Y_{kt} − \mu_k)(Y_{2t} − \mu_2)] & \cdots & \text{E}[(Y_{kt} − \mu_k)^2] \\ \end{bmatrix} \\\\ & \text{Covariance Diagonal} D = \text{diag}(\sqrt{\Gamma_{11}}, \cdots, \sqrt{\Gamma_{kk}}) \\\\ &\text{Cross-correlation Matrix}\rho(l) = D^{−1}\Gamma(l)D^{−1} \\ \end{align*}\]2) 임펄스 응답 함수(Impulse Response Function):
- for 각 변수가 다른 변수에 어떤 영향을 주는지 파악
(4) Example
-
\(Y_{1t} = 5 + 0.2 Y_{1t-1} + 0.3 Y_{2t-1} + e_{1t}\).
-
\(Y_{2t} = 3 - 0.6 Y_{1t-1} + 1.1 Y_{2t-1} + e_{2t}\).
[ Step 1 ] 차수 입력
intercept = np.array([5, 3])
matrix_A = np.array([[[0.2, 0.3],
[-0.6, 1.1]]])
residual_covariance = np.array([[1, 0.8],
[0.8, 2]])
[ Step 2 ] 데이터 생성
fit = statsmodels.tsa.vector_ar.var_model.VARProcess(matrix_A, intercept,
residual_covariance)
[ Step 3 ] 시뮬레이션
simul_num = 100
( 시각화 1 )
fit.plotsim(steps=simul_num, seed=123)
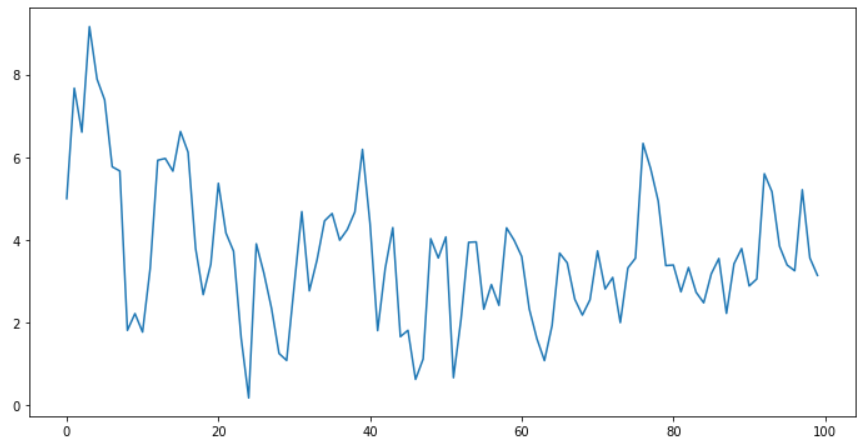
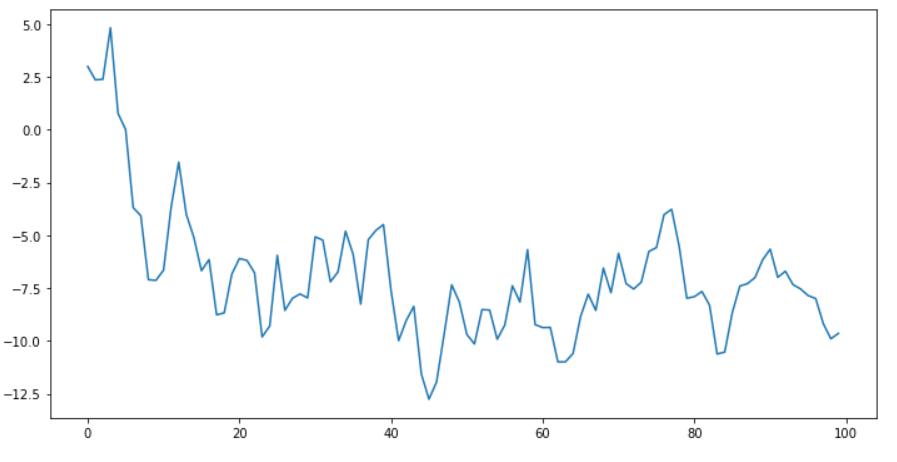
( 시각화 2 )
simul_values = statsmodels.tsa.vector_ar.util.varsim(fit.coefs, fit.intercept,
fit.sigma_u, steps=simul_num)
plt.plot(simul_values)
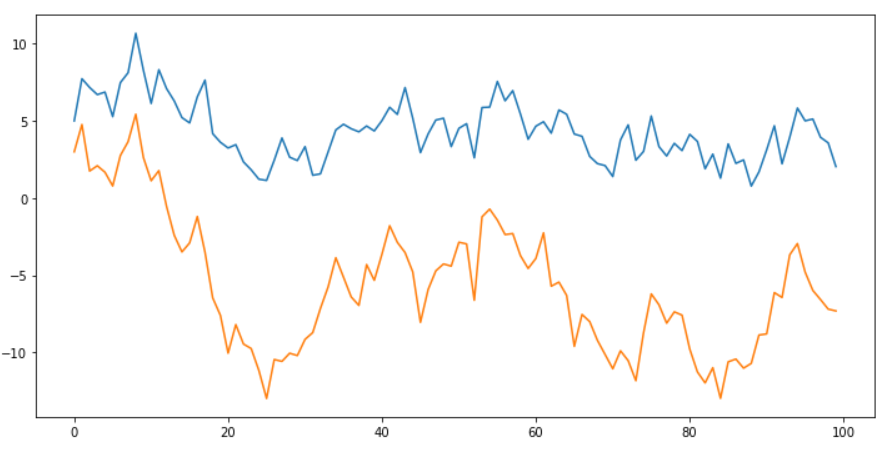
[ Step 4 ] ACF 시각화
fit.plot_acorr()
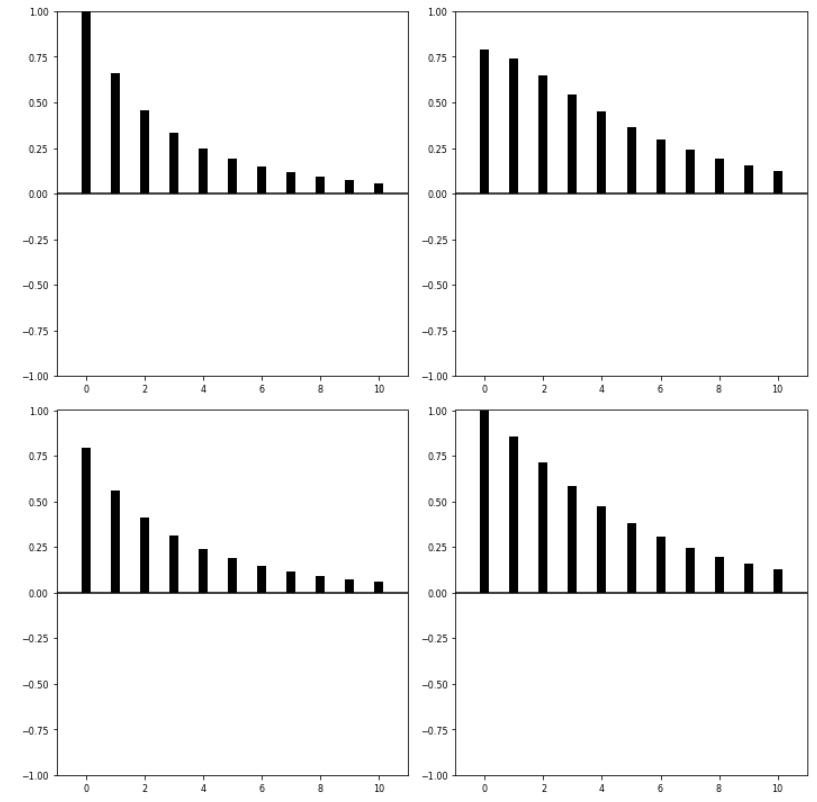
[ Step 5 ] VAR 모델에 fitting 시키기
fit = sm.tsa.VAR(simul_values).fit()
display(fit.summary())
Summary of Regression Results
==================================
Model: VAR
Method: OLS
Date: Wed, 01, Sep, 2021
Time: 15:28:38
--------------------------------------------------------------------
No. of Equations: 2.00000 BIC: 0.750992
Nobs: 99.0000 HQIC: 0.657348
Log likelihood: -304.339 FPE: 1.81076
AIC: 0.593712 Det(Omega_mle): 1.70582
--------------------------------------------------------------------
Results for equation y1
========================================================================
coefficient std. error t-stat prob
------------------------------------------------------------------------
const 5.953143 0.765180 7.780 0.000
L1.y1 0.071001 0.114198 0.622 0.534
L1.y2 0.344856 0.050679 6.805 0.000
========================================================================
Results for equation y2
========================================================================
coefficient std. error t-stat prob
------------------------------------------------------------------------
const 4.025728 1.062425 3.789 0.000
L1.y1 -0.714895 0.158559 -4.509 0.000
L1.y2 1.180274 0.070366 16.773 0.000
========================================================================
Correlation matrix of residuals
y1 y2
y1 1.000000 0.590427
y2 0.590427 1.000000
[ Step 6 ] 예측 & 시각화
forecast_num = 20
pred_var = fit.forecast(fit.model.endog[-1:], steps=forecast_num)
pred_var_ci = fit.forecast_interval(fit.model.endog[-1:], steps=forecast_num)
fit.plot_forecast(forecast_num)
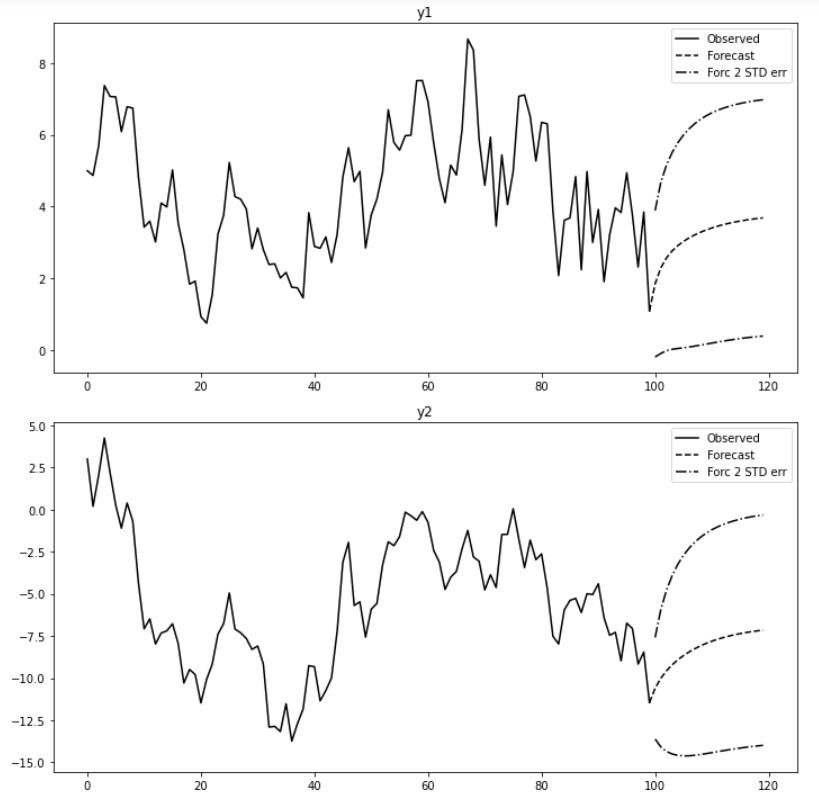
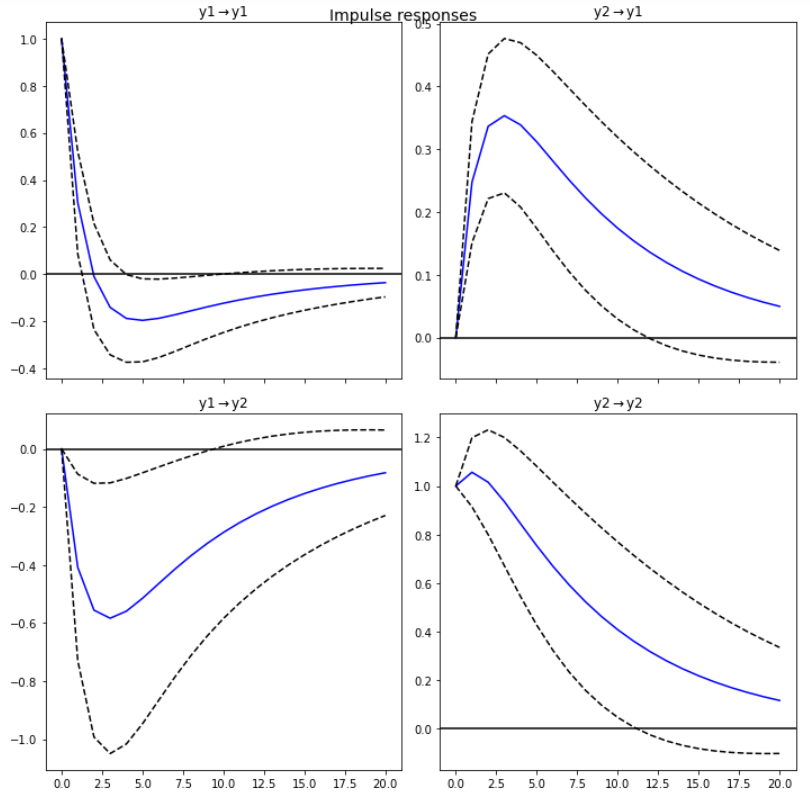
[ Step 7 ] Impulse 반응함수 추정
fit.irf(forecast_num).plot()