58.Stochastic Backpropagation and Approximate Inference in Deep Generative Models (2014)

Stochastic Backpropagation and Approximate Inference in Deep Generative Models ( 2014 )

Abstract

이 논문은 posterior distribution을 근사히기 위한 recognition model을 소개하고, stochastic backpropagation이 어떻게 작동하는지에 대해 설명한다.

1. introduction

accurate하면서도 scalable한 probabilistic model을 만드는 것은 ML에서 중요한 부분이다. 그 중에서도, 최근에 generative model에 대한 연구가 있어왔다. 그 중 대표적인 것은, directed model인 belief networks이다. 하자만 efficiency에서는 아쉬움이 있어왔다. 그 이후로도, 아래의 3가지를 만족시키는 generative model을 만들고자하는 노력들이 있어왔다.

• 1) DEEP ( data의 복잡한 구조를 포착하기 위해 )

• 2) FAST

• 3) COMPUTATIONALLY TRACTABLE & SCALABLE to high dimensional data

이 논문에서 제안하는 알고리즘은, deep, directed generative models with Gaussian latent variables at each layer를 소개함으로써, 위의 조건들을 충족시킨다.

이 모델은, 다음과 같은 2가지 세부 model을 사용한다,

• generative model ( decoder 역할 )
• recognition model ( encoder 역할 )

이러한 구조 속에서, backpropagation을 수정하여 entire한 모델을 train하고자 한다.

( 두 model의 parameter를 JOINTLY하게 optimize한다)

해당 논문의 contribution은 아래와 같다.

• combine DNN + probabilistic latent variable model

• scalable variational inference

  ( variational parameter & model parameter의 joint optimization )

• comprehensive and systematic evaluation of the model

2. DLGM (Deep Latent Gaussian Model)

DLGM은, 각각의 layer마다 Gaussian latent varaible을 가진 deep directed graphical model이다.

model로부터 데이터를 샘플(generate)하기 위해, 가장 먼저 top-most layer \(L\)의 Gaussian distribution에서 샘플을 한다. 그런 뒤 그것이 밑으로 쭈욱 타고 내려온다. 수식을 통한 이해가 더 쉬울 것 같아서, 아래의 식을 통해, 데이터가 generate되는 과정을 대략적으로 살펴보자.

\(\begin{aligned} \xi_{l} & \sim \mathcal{N}\left(\boldsymbol{\xi}_{l} \mid \mathbf{0}, \mathbf{I}\right), \quad l=1, \ldots, L \\ \mathbf{h}_{L} &=\mathbf{G}_{L} \boldsymbol{\xi}_{L} \\ \mathbf{h}_{l} &=T_{l}\left(\mathbf{h}_{l+1}\right)+\mathbf{G}_{l} \boldsymbol{\xi}_{l}, \quad l=1 \ldots L-1 \\ \mathbf{v} & \sim \pi\left(\mathbf{v} \mid T_{0}\left(\mathbf{h}_{1}\right)\right) \end{aligned}\).

• 위 식에서, \(T_l\)은 MLP (Multi-layer perceptron)이다.
• 마지막으로, distribution \(\pi ( v \mid \cdot)\)을 통해 data가 generate됨으로써 끝이난다.

우리는 generative model의 파라미터를 \(\theta^g\)라고 표기할 것이다.

그리고 이 파라미터에는 다음과 같은 Gaussian prior를 씌울 것이다.

\(p\left(\boldsymbol{\theta}^{g}\right)=\mathcal{N}(\boldsymbol{\theta} \mid \mathbf{0}, \kappa \mathbf{I})\).

이 모델의 joint pdf는 다음과 같이 2가지로 표현될 수 있다.

\(\begin{array}{l} p(\mathbf{v}, \mathbf{h})=p\left(\mathbf{v} \mid \mathbf{h}_{1}, \theta^{g}\right) p\left(\mathbf{h}_{L} \mid \boldsymbol{\theta}^{g}\right) p\left(\boldsymbol{\theta}^{g}\right) \prod_{l=1}^{L-1} p_{l}\left(\mathbf{h}_{l} \mid \mathbf{h}_{l+1}, \boldsymbol{\theta}^{g}\right) \\ p(\mathbf{v}, \boldsymbol{\xi})=p\left(\mathbf{v} \mid \mathbf{h}_{1}\left(\boldsymbol{\xi}_{1 \ldots L}\right), \boldsymbol{\theta}^{g}\right) p\left(\boldsymbol{\theta}^{g}\right) \prod_{l=1}^{L} \mathcal{N}(\boldsymbol{\xi} \mid \mathbf{0}, \mathbf{I}) \end{array}\).

• mean \(\boldsymbol{\mu}_{l}=T_{l}\left(\mathbf{h}_{l+1}\right)\) .
• covariance \(\mathbf{S}_{l}=\mathbf{G}_{l} \mathbf{G}_{l}^{\top}\).

위의 첫번째 표현을, 그림으로 나타내면 아래의 (a)와 같다.

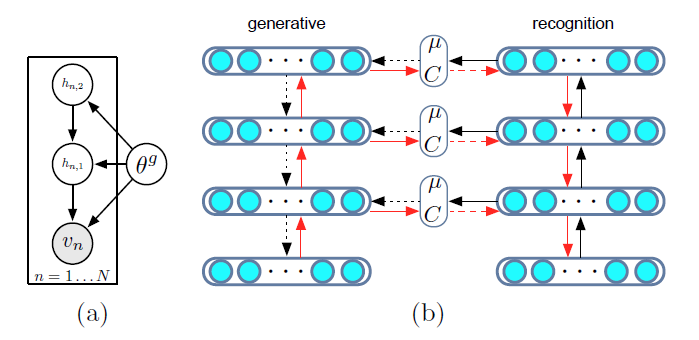
DLGM의 특징

• 하나의 layer만을 가지고 , \(T(\cdot)\)을 linear mapping으로 가정한 DLGM은 곧 factor analysis이다
• \(T_l(h) = \mathbf{A}_l f(\mathbf{h}) + \mathbf{b}_l\)이고, \(f\)를 simple elementwise non-linearty로 가정한 DLGM은 곧 non-linear Gaussian belief network이다.

우리의 목표는 위의 inference를 tractable하게 푸는 것이다. 그러기 위해 나온 방법들에는, mean-field variational EM, wake-sleep algorithm, SVI 등이 있다. 이 논문은, SVI를 따르지만, 약간의 변형을 줌으로써 이 알고리즘이 scalable하면서도 efficient하게끔 만든다.

3. Stochastic Backpropagation

gradient descent method는 \(\nabla_{\theta}\mathbf{E}_{q_{\theta}}[f(\xi)]\)에 대한 계산을 요구한다. 하지만 이것은 아래와 같은 2가지 이유로 직접적으로 계산하기 어렵다

• 1) expectation이 unknown이다
• 2) expectation이 이루어지는 파라미터 \(q\)에 대해 indirect dependency를 가지고 있다.

따라서, 이를 풀고자 제안하는 방법이 바로 Stochastic Backpropagation이다.

3-1. Gaussian Backpropagation (GBP)

\(\nabla_{\theta}\mathbf{E}_{q_{\theta}}[f(\xi)]\)를 mean과 covariance에 대해 미분한 값은 아래와 같다.

• \(\nabla_{\mu_{i}} \mathbb{E}_{\mathcal{N}(\mu, \mathrm{C})}[f(\boldsymbol{\xi})]=\mathbb{E}_{\mathcal{N}(\mu, \mathrm{C})}\left[\nabla_{\xi_{i}} f(\boldsymbol{\xi})\right]\).
• \(\nabla_{C_{i j}} \mathbb{E}_{\mathcal{N}(\mu, \mathrm{C})}[f(\boldsymbol{\xi})]=\frac{1}{2} \mathbb{E}_{\mathcal{N}(\mu, \mathrm{C})}\left[\nabla_{\xi_{i}, \xi_{j}}^{2} f(\boldsymbol{\xi})\right]\).

위 두식을 합치고, chain rule을 사용하여, gradient를 아래와 같이 구할 수 있다.

\(\nabla_{\theta} \mathbb{E}_{\mathcal{N}(\mu, \mathrm{C})}[f(\boldsymbol{\xi})]=\mathbb{E}_{\mathcal{N}(\mu, \mathrm{C})}\left[\mathrm{g}^{\top} \frac{\partial \boldsymbol{\mu}}{\partial \boldsymbol{\theta}}+\frac{1}{2} \operatorname{Tr}\left(\mathbf{H} \frac{\partial \mathbf{C}}{\partial \boldsymbol{\theta}}\right)\right]\).

• \(\mathrm{g}\) : gradient of the function \(f(\boldsymbol{\xi})\)

• \(\mathbf{H}\) : Hessian of the function \(f(\boldsymbol{\xi})\)

• 만약 \(C\)가 상수라면, 이는 곧 우리가 일반적으로 아는 Backpropagation이다
• \(\mathbf{H}\)를 구하고자하면, \(O(K^3)\)만큼의 연산량이 필요하다. 이를 quadratic하게 줄이는 방법에 대해서 뒤에서 이야기할 것이다.

3-2. Generalized Backpropagation Rules

Using the product rule for integrals

exponential family를 따르는 분포으 ㅣ특징으로, 우리는 아래를 충족시키는 \(B(\boldsymbol{\xi} ; \boldsymbol{\theta})\)를 찾을 수 있다.

\(\nabla_{\theta} \mathbb{E}_{p(\xi \mid \theta)}[f(\xi)]=-\mathbb{E}_{p(\xi \mid \theta)}\left[\nabla_{\xi}[B(\xi ; \theta) f(\xi)]\right]\).

( 자세한 것은 appendix 참조)

Using the suitable co-ordinate transformations

다음과 같은 transformation을 통해, \(R\)에 대한 gradient의 expectation을 다음과 같이 구할 수 있다.

• \(\mathcal{N}(\boldsymbol{\mu}, \mathbf{C})\), \(\boldsymbol{\epsilon} \sim \mathcal{N}(\mathbf{0}, \mathbf{I})\).
• \(y=\boldsymbol{\mu}+\mathbf{R} \boldsymbol{\epsilon}\) and \(\mathbf{C}=\mathbf{R} \mathbf{R}^{\top}\).

\(\rightarrow\) \(\begin{aligned} \nabla_{\mathbf{R}} \mathbb{E}_{\mathcal{N}(\mu, \mathrm{C})}[f(\boldsymbol{\xi})] &=\nabla_{\mathbf{R}} \mathbb{E}_{\mathcal{N}(0, I)}[f(\boldsymbol{\mu}+\mathbf{R} \boldsymbol{\epsilon})] =\mathbb{E}_{\mathcal{N}(0, I)}\left[\boldsymbol{\epsilon} \mathbf{g}^{\top}\right] \end{aligned}\).

4. Scalable Inference in DLGMs

\(V\)를 우리의 \(N \times D\) 크기의 observation집힙이라 하자 ( \(\mathbf{v}_n = [v_{n1},...,v_{nD}]^T\))

4-1. Free Energy Objective

Inference 문제를 풀기 위해, latent variable에 대해 integrate out해야하지만, 이는 intractable하기 때문에 우리는 ELBO를 maximize해야한다.

\(\begin{aligned} \mathcal{L}(\mathbf{V}) &=-\log p(\mathbf{V})=-\log \int p\left(\mathbf{V} \mid \boldsymbol{\xi}, \boldsymbol{\theta}^{g}\right) p\left(\boldsymbol{\xi}, \boldsymbol{\theta}^{g}\right) d \boldsymbol{\xi} \\ &=-\log \int \frac{q(\boldsymbol{\xi})}{q(\boldsymbol{\xi})} p\left(\mathbf{V} \mid \boldsymbol{\xi}, \boldsymbol{\theta}^{g}\right) p\left(\boldsymbol{\xi}, \boldsymbol{\theta}^{g}\right) d \boldsymbol{\xi} \\ &\leq D_{K L}[q(\boldsymbol{\xi}) \| p(\boldsymbol{\xi})]-\mathbb{E}_{q}\left[\log p\left(\mathbf{V} \mid \boldsymbol{\xi}, \boldsymbol{\theta}^{g}\right) p\left(\boldsymbol{\theta}^{g}\right)\right] \\ &=\mathcal{F}(\mathbf{V}) \end{aligned}\).

• ELBO의 1번째 term : KL divergence
• ELBO의 2번째 term : reconstruction error

간소화를 위해, 우리는 recognition model \(q(\xi \mid \mathbf{v})\)가, \(L\)개의 layer에 거쳐 factorize되는 Gaussian 분포를 띈다고 가정한다.

( recognition model은 generative model과 independent하다 )

\(q\left(\boldsymbol{\xi} \mid \mathbf{V}, \boldsymbol{\theta}^{r}\right)=\prod_{n=1}^{N} \prod_{l=1}^{L} \mathcal{N}\left(\boldsymbol{\xi}_{n, l} \mid \boldsymbol{\mu}_{l}\left(\mathbf{v}_{n}\right), \mathbf{C}_{l}\left(\mathbf{v}_{n}\right)\right)\).

• 여기서 \(\boldsymbol{\theta}^{r}\)는 \(q\) distribution의 parameter이다.

Gaussian prior와 Gaussian recognition model 가정 하에서, 위 ELBO식의 KL-divergence term은 analytically 풀린다.

이를 정리하면, 아래와 같다.

$$D_{K L}[\mathcal{N}(\boldsymbol{\mu}, \mathbf{C}) | \mathcal{N}(\mathbf{0}, \mathbf{I})]=\frac{1}{2}\left[\operatorname{Tr}(\mathbf{C})-\log

\mathbf{C}

+\boldsymbol{\mu}^{\top} \boldsymbol{\mu}-D\right]$$.

\(\mathcal{F}(\mathbf{V})=-\sum_{n} \mathbb{E}_{q}\left[\log p\left(\mathbf{v}_{n} \mid \mathbf{h}\left(\boldsymbol{\xi}_{n}\right)\right)\right]+\frac{1}{2 \kappa}\left\|\boldsymbol{\theta}^{g}\right\|^{2}\).

기타

• 보다 나은 inference를 위해서 recognition model은 flexible해야한다
• additional noise를 통해 recognition model을 regularize할 필요가 있다
• ReLU등과 같은 non-linear activation function을 사용하는 것이 좋다.

4-2. Gradients of the Free Energy

위에서 구한 ELBO ( \(\mathcal{F}(\mathbf{V})=-\sum_{n} \mathbb{E}_{q}\left[\log p\left(\mathbf{v}_{n} \mid \mathbf{h}\left(\boldsymbol{\xi}_{n}\right)\right)\right]+\frac{1}{2 \kappa}\left\|\boldsymbol{\theta}^{g}\right\|^{2}\) )를 maximize하기 위해, 우리는 Monte Carlo방법을 사용한다.

\(\mathcal{F}(\mathbf{V})\)를 generative model의 parameter \(\theta_j^g\)와 , recognition model의 parameter \(\theta_j^r\)에 대해 미분하면, 각각 아래와 같이 정리된다.

• [generative model] \(\nabla_{\theta_{j}^{g}} \mathcal{F}(\mathbf{V})=-\mathbb{E}_{q}\left[\nabla_{\theta_{j}^{g}} \log p(\mathbf{V} \mid \mathbf{h})\right]+\frac{1}{\kappa} \theta_{j}^{g}\).

• [recognition model]

  • \(\nabla_{\mu_{l}} \mathcal{F}(\mathbf{v}) =-\mathbb{E}_{q}\left[\nabla_{\boldsymbol{\xi}_{l}} \log p(\mathbf{v} \mid \mathbf{h}(\xi))\right]+\boldsymbol{\mu}_{l}\).
  • \(\begin{aligned} \nabla_{R_{l, i, j}} \mathcal{F}(\mathbf{v}) =-\frac{1}{2} \mathbb{E}_{q}\left[\epsilon_{l, j} \nabla_{\xi_{l, i}} \log p(\mathbf{v} \mid \mathbf{h}(\boldsymbol{\xi}))\right] &+\frac{1}{2} \nabla_{R_{l, i, j}}\left[\operatorname{Tr} \mathbf{C}_{n, l}-\log \left|\mathbf{C}_{n, l}\right|\right] \end{aligned}\).

  \(\rightarrow\) 위 두 식을 통해, \(\nabla_{\boldsymbol{\theta}^{r}} \mathcal{F}(\mathbf{v})=\nabla_{\boldsymbol{\mu}} \mathcal{F}(\mathbf{v})^{\top} \frac{\partial \boldsymbol{\mu}}{\partial \boldsymbol{\theta}^{r}}+\operatorname{Tr}\left(\nabla_{\mathbf{R}} \mathcal{F}(\mathbf{v}) \frac{\partial \mathbf{R}}{\partial \boldsymbol{\theta}^{r}}\right)\).

( 위의 정리된 식에서, Recognition parameter에 대해서 미분 값을 구하려면Gaussian Backpropagation을 사용해야 한다. Hessian matrix의 \(O(K^3)\) 연산량 문제를 해결 하기 위해, co-ordinate transformation을 사용해야한다. 즉, \(C\)를 사용하는 것이 아니라, \(C=RR^T\)의 \(R\)을 사용해야 한다. )

알고리즘을 요약하자면, ( 위의 figure 1의 (b)를 참고하라 )

• 1) 가장 먼저 forward pass를 한다. (black arrow)
  • bottom-up phase (recognition)
  • top-down phase (generative)
• 2) 그 다음에 backward pass를 한다 (red arrows)
  • gradients들은 계산된다.
  • descent step : \(\Delta \theta^{g, r}=-\Gamma^{g, r} \nabla_{\theta^{g}, r} \mathcal{F}(\mathbf{V})\).