[Explicit DGM] 04. VAE

[Explicit DGM] 04. VAE

( 참고 : KAIST 문일철 교수님 : 한국어 기계학습 강좌 심화 2)

Contents

1. VAE 소개
2. Objective Function of VAE
3. Reparameterization Trick
4. ELBO of Gaussian VAE
5. 정리

1. VAE 소개

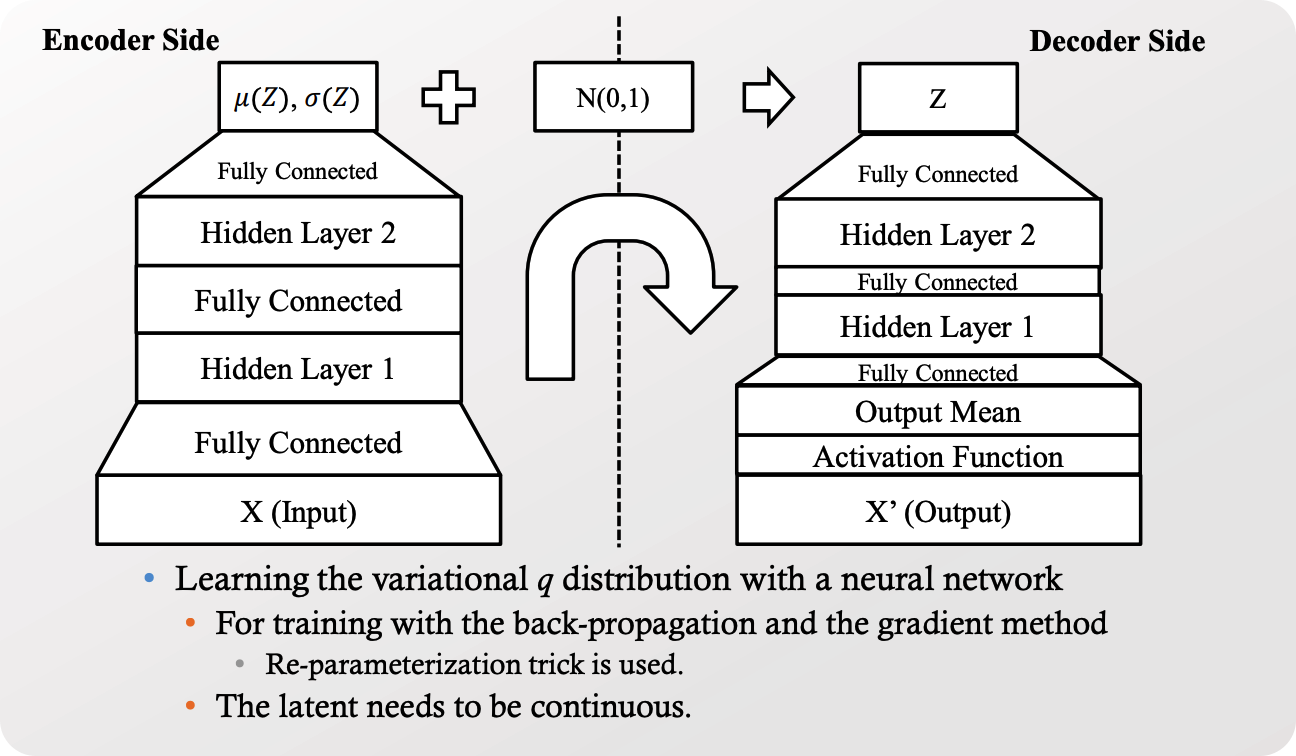
VAE = PROBABILISTIC autoencoder

• 데이터 생성/복원 과정에서 stochasticity가 부여된다.

  ( Denoising Autoencoder에서는, 단지 input에만 부여되었었다 )

목적함수 concept : (1) + (2)

• (1) regularizer

  • variational distribution \(q\) 가 지나치게 complex하지 않도록 규제

    ( = prior와 유사하도록 규제 )

• (2) (negative) reconstruction error

  • input을 잘 복원하도록

2. Objective Function of VAE

목적함수 :

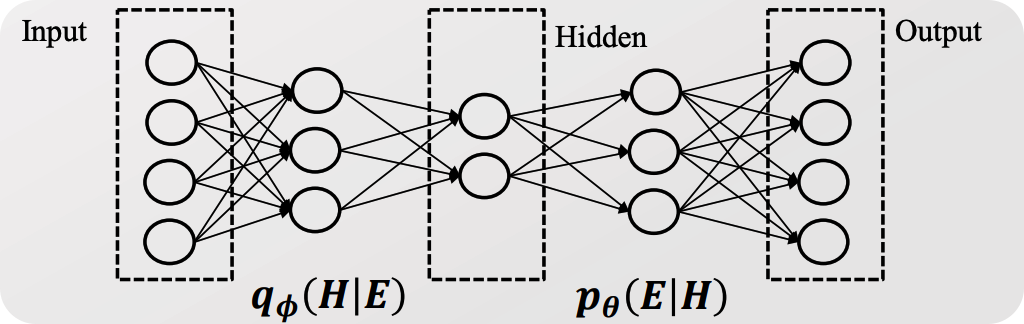
• \(\mathcal{L}=-D_{K L}\left(q_{\phi}(H \mid E) \mid \mid p_{\theta}(H)\right)+\mathbb{E}_{q_{\phi}(H \mid E)}\left[\log p_{\theta}(E \mid H)\right]\).
  • (1) regularize : \(-D_{K L}\left(q_{\phi}(H \mid E) \mid \mid p_{\theta}(H)\right)\).
  • (2) (negative) reconstruction error : \(\mathbb{E}_{q_{\phi}(H \mid E)}\left[\log p_{\theta}(E \mid H)\right]\)
• 해석
  • (1)의 \(q_{\phi}\) : \(E\) 로부터 \(H\)를 생성 ( = encode )
  • (2)의 \(p_{\theta}\) : \(H\) 로부터 \(E\)를 생성 ( = decode )

3. Reparameterization Trick

(복습) ELBO 식 :

• \(\mathbb{E}_{q_{\phi}(z \mid x)}\left[\log p_{\theta}(x \mid z)\right]-D_{K L}\left(q_{\phi}(z \mid x) \mid \mid p_{\theta}(z)\right)\).

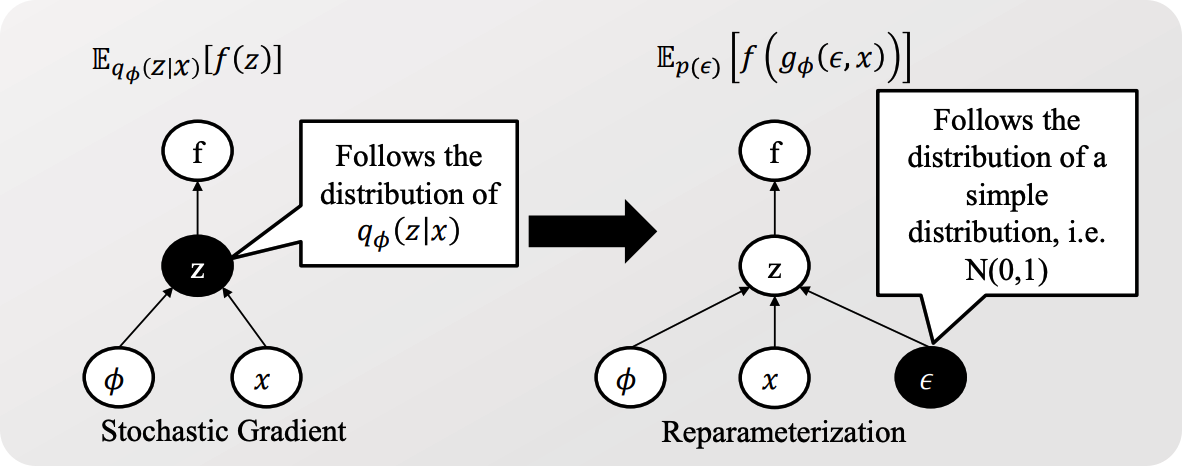
위 식에서, \(q_{\phi}(z \mid x)\) 는 stochastic 하다. 따라서, back-prop시 문제가 발생한다.

이를 위해 사용하는 것이 reparameterization trick 이다.

Reparameterization Trick

\(\tilde{z} \sim q_{\phi}(z \mid x): \tilde{z}=g_{\phi}(\epsilon, x)\), with \(\epsilon \sim p(\epsilon)\)

• stochastic (s), deterministic (d)
  • s = d(mu) + s(noise)*d(std)

여기세, Amortized Inference를 적용하면,

• \(q(H \mid E ; \phi)=\prod_{i} q\left(H_{i} ; N N_{i}\left(E ; \phi_{i}\right)\right)\).

예시 ( Normal distn의 평균 & 분산을 모델)

• \(q_{\phi}(z \mid x) \sim N(\mu(x ; \phi), \Sigma(x ; \phi))\).
• \(g_{\phi}(\epsilon, x)=\mu(x ; \phi)+e \sqrt{\Sigma(x ; \phi)}, e \sim N(0,1)\).
  • \(\mu_{i}(x ; \phi)=N N_{i}^{\mu}\left(x \mid E ; \phi_{i}^{\mu}\right)\) .
  • \(\Sigma_{i}(x ; \phi)=N N_{i}^{\Sigma}\left(x \mid E ; \phi_{i}^{\Sigma}\right)\).

계산 방법 ( Monte Carlo Sampling 통해 )

• 여러 개의 noise를 샘플링해서 expectation값을 근사한다.

• \(\mathbb{E}_{q_{\phi}(z \mid x)}[f(z)]=\mathbb{E}_{p(\epsilon)}\left[f\left(g_{\phi}(\epsilon, x)\right)\right] \approx \frac{1}{D} \sum_{d=1}^{D} f\left(g_{\phi}\left(\epsilon^{(d)}, x\right)\right)\),
  • where \(\epsilon^{(d)} \sim p(\epsilon)\)
• 이것을, ELBO 식에 적용할 경우…
  • \(\tilde{\mathcal{L}}=\frac{1}{D} \sum_{d=1}^{D}\left(\log p_{\theta}\left(x \mid z^{(d)}\right)\right)-D_{K L}\left(q_{\phi}(z \mid x) \mid \mid p_{\theta}(z)\right)\),
    • where \(z^{(d)}=g_{\phi}\left(\epsilon^{(d)}, x^{(d)}\right)\) and \(\epsilon^{(d)} \sim p(\epsilon)\)

4. ELBO of Gaussian VAE

ELBO : \(\mathcal{L}=-D_{K L}\left(q_{\phi}(H \mid E) \mid \mid p_{\theta}(H)\right)+\mathbb{E}_{q_{\phi}(H \mid E)}\left[\log p_{\theta}(E \mid H)\right]\).

ELBO = TERM 1 + TERM 2

• TERM 1 : KL-divergence
• TERM 2 : Expectation

VAE의 variational distribution을 Gaussian으로 모델링해보자

( 즉, \(\mu\) & \(\Sigma\) 를 추정하는 상황을 가정하자. )

• variational distribution : \(q_{\phi}(H \mid E) \sim N\left(\mu, \sigma^{2} I\right)\)
• prior : \(p_{\theta}(H) \sim N(0, I)\)

(1) TERM 1 : KL-divergence

위를 활용하여, ELBO의 첫 번째 term인 KL-divergence 를 정리하면 아래와 같다.

\(\begin{aligned} D_{K L} &\left(q_{\phi}(H \mid E) \mid \mid p_{\theta}(H)\right)\\&=-\int q_{\phi}(H \mid E) \log p_{\theta}(H) d H+\int q_{\phi}(H \mid E) \log q_{\phi}(H \mid E) d H \\ &= (1) + (2) \end{aligned}\).

\[\begin{aligned} (1) &= -\int q_{\phi}(H \mid E) \log p_{\theta}(H) d H \\&=-\int q_{\phi}(H \mid E) \log \frac{1}{\left(2 \pi(1)^{2}\right)^{\frac{1}{2}}} \exp \left(-\frac{(H-0)^{2}}{2(1)^{2}}\right) d H \\ &=-\int q_{\phi}(H \mid E) \log \frac{1}{\left(2 \pi(1)^{2}\right)^{\frac{1}{2}}} d H-\int q_{\phi}(H \mid E)\left\{-\frac{(H-0)^{2}}{2(1)^{2}}\right\} d H \\ &=-\log \frac{1}{\left(2 \pi(1)^{2}\right)^{\frac{1}{2}}} \int q_{\phi}(H \mid E) d H+\int \frac{1}{2} H^{2} q_{\phi}(H \mid E) d H=\frac{1}{2} \log 2 \pi+\int \frac{1}{2} H^{2} q_{\phi}(H \mid E) d H \\ &=\frac{1}{2} \log 2 \pi+\frac{1}{2}\left(\sigma^{2}+\mu^{2}\right) \end{aligned}\]

• \(\sigma^{2}=\int H^{2} q_{\phi}(H \mid E) d H-\left\{\int H^{2} q_{\phi}(H \mid E) d H\right\}^{2}=\int H^{2} q_{\phi}(H \mid E) d H-\mu^{2} \rightarrow \int H^{2} q_{\phi}(H \mid E) d H=\sigma^{2}+\mu^{2}\).

\(\begin{aligned} (2) &=\int q_{\phi}(H \mid E) \log q_{\phi}(H \mid E) d H \\& =\int q_{\phi}(H \mid E) \log \frac{1}{\left(2 \pi \sigma^{2}\right)^{\frac{1}{2}}} \exp \left(-\frac{(H-\mu)^{2}}{2 \sigma^{2}}\right) d H \\ &=\int q_{\phi}(H \mid E) \log \frac{1}{\left(2 \pi \sigma^{2}\right)^{\frac{1}{2}}} d H+\int q_{\phi}(H \mid E)\left\{-\frac{H^{2}-2 \mu H+\mu^{2}}{2 \sigma^{2}}\right\} d H \\ &=-\frac{1}{2} \log 2 \pi \sigma^{2}-\frac{1}{2 \sigma^{2}}\left\{\int H^{2} q_{\phi}(H \mid E) d H-2 \mu \int H q_{\phi}(H \mid E) d H+\mu^{2} \int q_{\phi}(H \mid E) d H\right\} \\ &=-\frac{1}{2} \log 2 \pi \sigma^{2}-\frac{1}{2 \sigma^{2}}\left\{\sigma^{2}+\mu^{2}-2 \mu \times \mu+\mu^{2}\right\} \\& =-\frac{1}{2} \log 2 \pi \sigma^{2}-\frac{1}{2}\\&=-\frac{1}{2} \log 2 \pi-\log \sigma-\frac{1}{2} \end{aligned}\).

• \(\sigma^{2}=\int H^{2} q_{\phi}(H \mid E) d H-\left\{\int H^{2} q_{\phi}(H \mid E) d H\right\}^{2}=\int H^{2} q_{\phi}(H \mid E) d H-\mu^{2} \rightarrow \int H^{2} q_{\phi}(H \mid E) d H=\sigma^{2}+\mu^{2}\).

정리하자면,

• (1) \(\frac{1}{2} \log 2 \pi+\frac{1}{2}\left(\sigma^{2}+\mu^{2}\right)\)

• (2) \(-\frac{1}{2} \log 2 \pi-\log \sigma-\frac{1}{2}\)

• KL-divergence ( \(D_{K L} \left(q_{\phi}(H \mid E) \mid \mid p_{\theta}(H)\right)\) )

  = (1) + (2)

  = \(\frac{1}{2}\left(\sigma^{2}+\mu^{2} -1 \right) - \log \sigma\)

(2) TERM 2 : Expectation

\(\mathbb{E}_{q_{\phi}(H \mid E)}\left[\log p_{\theta}(E \mid H)\right] =\frac{1}{D} \sum_{d=1}^{D}\left(\log p_{\theta}\left(E \mid H^{(d)}\right)\right) =\frac{1}{D} \sum_{d=1}^{D}\left(\log p_{\theta}\left(E \mid E^{(d)}\right)\right)\).

• 왜냐하면, VAE의 decoder는 deterministic 하게 \(H^{(d)}\)에서 \(E^{(d)}\) 로 projection 하기 때문이다. ( stochasticity는 encoding 과정에서 발생한다 )

\(\log p_{\theta}\left(E \mid E^{(d)}\right)\).

• \(E_i\) 가 continuous 한 경우 : ex) Normal
  • \(p_{\theta}\left(E_{i} \mid E_{i}^{(d)}\right) \sim \mathrm{N}\left(E_{i}^{(d)}, 1^{2}\right)\).
  • 따라서, \(\log p_{\theta}\left(E \mid E^{(d)}\right)=C \times \log \exp \left(-\frac{\left(E_{i}-E_{i}^{(d)}\right)^{2}}{2}\right)=-C \times\left(E_{i}-E_{i}^{(d)}\right)^{2}\).
• \(E_i\) 가 discrete 한 경우 : ex) Bernoulli
  • \(p_{\theta}\left(E_{i} \mid E_{i}^{(d)}\right) \sim \operatorname{Bern}\left(E_{i}^{(d)}\right)\).
  • 따라서, \(\log p_{\theta}\left(E \mid E^{(d)}\right)=\log \left\{E^{(d)^{E_{i}}}\left(1-E^{(d)}\right)^{1-E_{i}}\right\}=E_{i} \log E^{(d)}+\left(1-E_{i}\right) \log \left(1-E^{(d)}\right)\)

5. 정리