05.[paper review] BPR from Implicit Feedback

[ Recommender System ]

( 참고 : Fastcampus 추천시스템 강의 )

5. [paper review] Bayesian Personalized Ranking from Implicit Feedback

1. Abstract

BPR : implicit feedback을 사용한 추천 시스템

• BPR-Opt 제안 ( Bayesian 방법을 사용한 최적화 기법 )

Contribution

• 1) Posterior를 maximize하는 BPR-Opt 제안
• 2) 기존의 SGD보다 뛰어난 성능
• 3) 당시의 SOTA 모델들에 적용

2. Introduction & Related Works

추천시스템을 구현하기 위한 데이터로 크게 다음과 같은 2가지 데이터가 있다,

• explicit 과 implicit

  ( implicit 데이터가 더 큰 비중을 차지하고, 풀기 어렵다 )

따라서 이 알고리즘은, user의 implicit한 feedback으로, 개인별 Ranking을 추천하는 방안을 제시한다.

( = Personalized Ranking )

3. Personalized Ranking

Key point

• User에게 Item Ranking List를 추천( = Item Reccomendation )
• Implicit feedback을 사용해서 추천
• Non-observed item ( = user-item ranking matrix에서 채워지지 않은 부분 )
  • 이 non-observed item은
    • 1) 좋아하지 않아서 응답하지 않은 것과 ( real negative feedback)
    • 2) 못 봐서(몰라서) 응답하지 않은 것 ( missing value ) 로 나눠서 볼 수 있다.

핵심은, user별로 personalized된 ranking을 구하는 것이다. 다른말로, user별로 좋아할 item의 순위를 산정해주는 것이다.

Notation :

• \(U\) : user 집합

• \(I\) : Item 집합

  \(\rightarrow\) user별로 personalized total ranking \(\left(>_{u} \subset I^{2}\right)\) 구하기

\(>_{u}\)의 특징

\[\begin{array}{lr}\forall i, j \in I: i \neq j \Rightarrow i>_{u} j \vee j>_{u} i & \text { (totality) } \\ \forall i, j \in I: i>_{u} j \wedge j>_{u} i \Rightarrow i=j & \text { (antisymmetry) } \\ \forall i, j, k \in I: i>_{u} j \wedge j>_{u} k \Rightarrow i>_{u} k & \text { (transitivity) }\end{array}\]

기존의 알고리즘

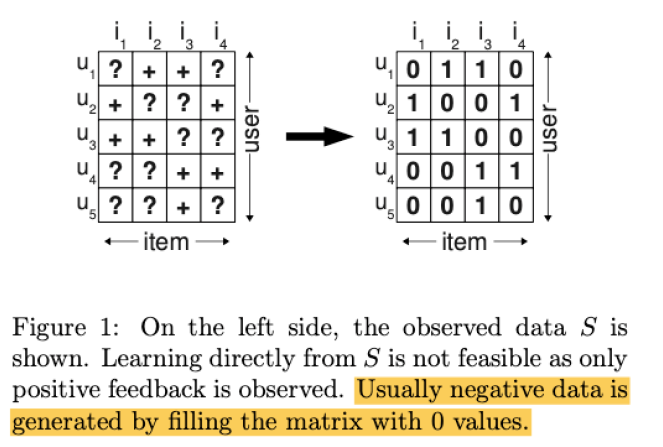
• (LEFT) \(?\) : 응답 없음 , \(+\) 응답 함

• (RIGHT) \(1\) : 응답있음 = 선호함, \(0\) : 응답없음=비선호함

BPR 알고리즘

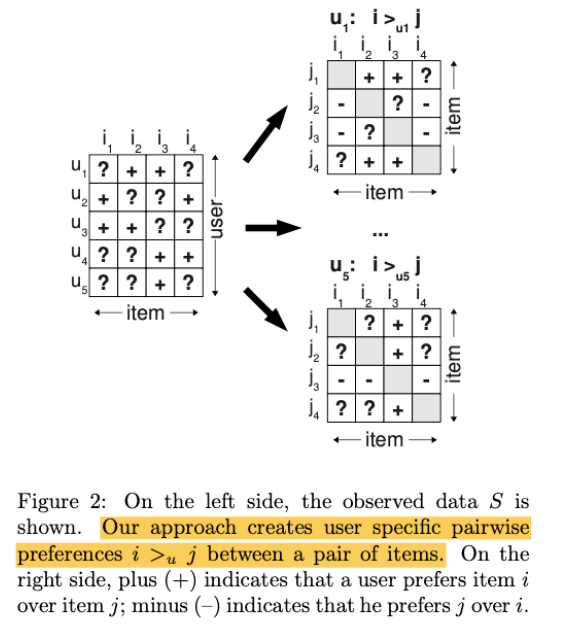
• Pair wise preference를 사용

  ( 즉, item \(i\)와 item \(j\)와의 선호를 비교한다 )

• (Left) Item x User matrix

  • \(+\) : 응답함
  • \(?\) : 응답 없음

• (Right) User개수 만큼의 Item x item matrix

  • \(+\) : 해당 matrix의 user가 item \(i\) > item \(j\)
  • \(-\) : 해당 matrix의 user가 item \(j\) > item \(i\)
  • \(?\) : 알수 없음

• training 데이터 : \(D_{s}:=\left\{(u, i, j) \mid i \in I_{u}^{+} \wedge j \in I \backslash I_{u}^{+}\right\}\)

  test 데이터 : missing values

4 . Bayesian Personalized Ranking (BPR)

Bayesian view : maximize posterior ( \(\propto\) likelihood \(\times\) prior )

4-1. BPR Optimization Criterion

By Bayes Rule..

\[p\left(\Theta \mid>_{u}\right) \propto p\left(>_{u} \mid \Theta\right) p(\Theta)\]

(a) Likelihood

\[\begin{aligned}\prod_{u \in U} p\left(>_{u} \mid \Theta\right)&=\prod_{(u, i, j) \in U \times I \times} p\left(i>_{u} j \mid \Theta\right)^{\delta\left((u, i, j) \in D_{s}\right)} \cdot\left(1-p\left(i>_{u} j \mid \Theta\right)\right)^{\delta\left((u, i, j) \notin D_{s}\right)} \\ &=\prod_{(u, i, j) \in D_{s}} p\left(i>_{u} j \mid \Theta\right) \\ &=\prod_{(u, i, j) \in D_{s}} \sigma\left(\widehat{x_{u i j}}(\Theta)\right) \end{aligned}\]

• by Totality & Antisymmetry
• where \(\delta(b):=\left\{\begin{array}{c} 1 \text { if } b \text { is true } \\ 0 \text { else } \end{array}\right.\)
• \(\widehat{x_{u i j}}\) : User \(u\)와 Item \(i,j\) 사이의 관계를 modeling한 parameter

(b) Prior

\(p(\Theta) \sim N\left(0, \Sigma_{\Theta}\right)\) where \(\Sigma_{\Theta}=\lambda_{\Theta} I\)

(c) Objective Function

위의 (a),(b)를 통해 우리는 posterior를 구할 수 있다.

우리가 maximize해야 하는 log posterior (BPR-Opt) 는 아래와 같이 정리될 수 있다.

( Prior로 인해 penalty term이 들어가서 regularizer의 역할을 확인하는 것을 알 수 있다. )

\(\begin{aligned} \text { BPR-OPT } &:=\ln p\left(\Theta \mid>_{u}\right) \\ &=\ln p\left(>_{u} \mid \Theta\right) p(\Theta) \\ &=\ln \prod_{(u, i, j) \in D_{S}} \sigma\left(\hat{x}_{u i j}\right) p(\Theta) \\ &=\sum_{(u, i, j) \in D_{S}} \ln \sigma\left(\hat{x}_{u i j}\right)+\ln p(\Theta) \\ &=\sum_{(u, i, j) \in D_{S}} \ln \sigma\left(\hat{x}_{u i j}\right)-\lambda_{\Theta}\ \mid\Theta\ \mid^{2} \end{aligned}\).

4-2. BPR Learning Algortihm

gradient w.r.t \(\theta\)는 다음과 같고,

\(\begin{aligned} \frac{\partial \mathrm{BPR}-\mathrm{OPT}}{\partial \Theta} &=\sum_{(u, i, j) \in D_{S}} \frac{\partial}{\partial \Theta} \ln \sigma\left(\hat{x}_{u i j}\right)-\lambda_{\Theta} \frac{\partial}{\partial \Theta}\ \mid\Theta\ \mid^{2} \\ & \propto \sum_{(u, i, j) \in D_{S}} \frac{-e^{-\hat{x}_{u i j}}}{1+e^{-\hat{x}_{u i j}}} \cdot \frac{\partial}{\partial \Theta} \hat{x}_{u i j}-\lambda_{\Theta} \Theta \end{aligned}\).

이를 통해 algorithm을 정리하자면 아래와 같이 나온다.

• Triples를 학습하는 Bootstrap 기반 SGD

  ( 데이터 수가 많기 떄문에 full data가 아닌 bootstrap sample만 사용해도 OK )

4-3. Learning models with BPR

아래의 두 가지 모델에 모두 적용 가능하며, 그 성능 또한 우수한 것으로 실험되었다.

(1) Matrix Factorization

\(\frac{\partial}{\partial \theta} \hat{x}_{u i j}=\left\{\begin{array}{ll} \left(h_{i f}-h_{j f}\right) & \text { if } \theta=w_{u f} \\ w_{u f} & \text { if } \theta=h_{i f} \\ -w_{u f} & \text { if } \theta=h_{j f} \\ 0 & \text { else } \end{array}\right.\).

(2) Adaptive KNN

\(\frac{\partial}{\partial \theta} \hat{x}_{u i j}=\left\{\begin{array}{ll} +1 & \text { if } \theta \in\left\{c_{i l}, c_{l i}\right\} \wedge l \in I_{u}^{+} \wedge l \neq i \\ -1 & \text { if } \theta \in\left\{c_{j l}, c_{l j}\right\} \wedge l \in I_{u}^{+} \wedge l \neq j \\ 0 & \text { else } \end{array}\right.\).

5. Conclusion

• Bayesian view (MAP)
• BPR-Opt제안 ( for Personalized Ranking )
• SGD ( using Bootstrap samples )
• MF, Adaptive KNN에 모두 적용 가능 + 성능 우수