Gaussian Process (1) Gaussian Process Regression

Gaussian Process (1)

( https://github.com/aailabkaist/Introduction-to-Artificial-Intelligence-Machine-Learning/blob/master/를 참고하여 공부하고 정리하였습니다 )

1. Introduction

Continuous Data

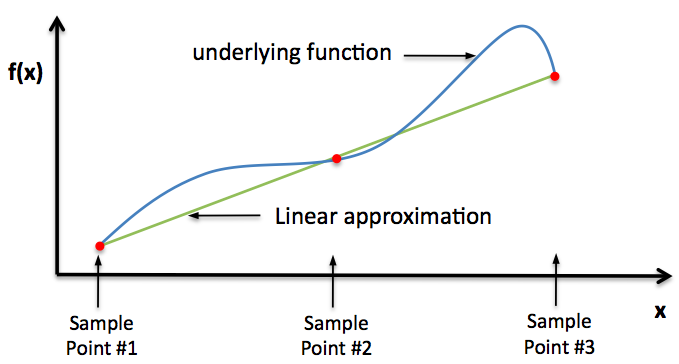
우리가 살고 있는 세상 속의 수 많은 데이터는 연속형(continuous) 데이터다. 시간, 장소 관련 데이터가 이에 속한다고 할 수 있다. 이러한 데이터를 어떻게 분석할 것인가? 대표적인 분석으로, 1) 해당 데이터를 만들어내는 잠재 되어있는 함수 (underlying function)에 대한 예측(estimation)이 있고, 또 다른 것으로는 2) 새로운 데이터에 대한 예측(prediction)이 있다.

Underlying Function

https://oceanai.mit.edu/ivpman/moos-ivp-doc/wiki/figs_ivpbuild/smart-gone-bad.png

주어진 데이터를 통해 그것의 underlying function을 어떻게 찾을 수 있을까?

관측된 데이터는, 2개의 함수로 의해 설명될 수 있다.

• 1 ) Mean Function
• 2 ) Variance Function

이전까지는, 우리는 mean과 variance를 하나의 값으로 생각했었다. 하지만 앞으로, 우리는 이를 하나의 점이 아니라 time t에 대한 일종의 함수라고 생각할 것이다.

example)

• BEFORE : \(N(3,2^2)\)
• AFTER : \(N(\mu(t),\sigma(t)^2)\)

Mapping function

한 문장으로 요약하자면, mapping function을 통해 basis를 확장할 수 있다. ( transformation function / basis function 이라고도 불린다 )

mapping/basis function \(\phi\) : \(L (low) \rightarrow H(high)\)

이를 통해, 주어진 데이터를 보다 복잡/다양하게 표현할 수 있다. 하지만 그만큼 공간 (feature space)가 커진다는 점도 같이 감안해야할 것이다.

example)

https://www.researchgate.net/publication/281412932/figure/

다음 그림을 보자. 왼쪽 그림 (a)의 빨간 점과 파란 점을 구분하기 위해, 다음과 같이 구불구불한 (non-linear) 선이 필요하다. 하지만 여기서 우리가 이 점들을 mapping function을 통해 2차원에서 3차원으로 확장할 경우 ( 오른쪽 그림의 (b) ), 우리는 하나의 초평면(hyperplane)으로 이 둘을 잘 구분할 수 있게 될 것이다. SVM을 공부해본 적 있다면 아마 쉽게 이해할 것이다.

이 정도의 개념만 알아두고 Gaussian Process에 대해 설명해보겠다.

2. Before Gaussian Process…

1) Linear Regression with Basis Function

다들 선형회귀 (Linear Regression)모델에 대해서 많이들 알 것이다. 이것을 Basis Function을 사용하여 다음과 같이 나타낼 수 있다.

\[y(x) = w^{T}\phi(x)\]

• \(w\) : weight vector
• \(\phi\) : design matrix ( input vector와 weight vector 간의 관계를 맺어준다 )

우리는 위 식을 다음과 같이 표현하기도 한다.

\[Y = \phi\; w\]

예를 들어, \(y=ax^2 + bx + c\)라는 단순한 2차식을 위의 형태로 표현해보자.

\[y = \begin{pmatrix} a\\ b\\ c \end{pmatrix}^T \begin{pmatrix} x^2\\ x\\ 1 \end{pmatrix}\]

위 표현에서, \(\phi(x) = (x^2,x,1)\) 이 된다.

우리는 이전까지 이 \(w\) 또한 고정적인 값(deterministic value)라고 생각했었다. 하지만, 우리는 앞으로 이 \(w\)를 하나의 확률분포에서 나온 값 (probabilistically distributed values)으로 생각할 것이다.

\[p(w) = N(w \mid 0, \alpha^{-1}I)\]

(여기서 \(\alpha^{-1}\) 은 분산을 뜻한다. 즉, precision은 \(\alpha\) )

\(w\)를 다음과 같이 확률 분포에 의한 값으로 설정할 경우, \(Y\) 또한 당연히 그러할 것이다. \(Y\)의 평균과 (공)분산은 다음과 같이 나타낼 수 있을 것이다.

\[E[Y] = E[\phi w] = \phi\;E[w] = 0\] \[\begin{align*} cov[Y] &= E[(Y-0)(Y-0)^{T}] = E[YY^T]\\ &= E[\phi w w^T \phi^T] = \phi E[ww^T]\phi^T\\ &= \frac{1}{\alpha}\phi\phi^T \end{align*}\]

이제 우리는 \(K\) matrix를 covariance matrix를 통해서 정의할 것이다.

\[K_{nm} = k(x_n,x_m) = \frac{1}{\alpha}\phi(x_n)^T\phi(x_m)\]

그러면, 우리는 \(Y\)의 분포를 다음과 같이 나타낼 수 있게 된다.

\[p(Y) = N(Y \mid 0, K)\]

2) Kernel Function

SVM에서 공부했던 내용이다. 커널(kernel)은 두 벡터의 내적을 다른(혹은 같은)차원의 공간으로 나타내주는 역할을 한다.

\[K(x_i,x_j) = \varphi(x_i)\cdot \varphi(x_j)\]

몇몇의 대표적인 kernel function들은 다음과 같다.

Polynomial (homogeneous)

\[k(x_i,x_j) = (x_i \cdot x_j)^d\]

Polynomial (inhomogeneous)

\[k(x_i,x_j) = (x_i \cdot x_j+1)^d\]

Gaussian kernel function ( RBF, Radial Basis Function )

\[k(x_i,x_j) = exp(-\gamma \mid \mid x_i - x_j \mid\mid^2)\]

( \(\gamma\) 로는 \(\frac{1}{2\sigma^2}\) 를 사용하는 경우가 많다 )

Hyperbolic tangent

\[k(x_i,x_j) = tanh(ux_i \cdot x_j + c)\]

3. Gaussian Process Regression

1) Modeling Noise with Gaussian Distribution

우리가 실제로 관측하게 되는 데이터는 error(noise)가 있을 수 밖에 없다. 그래서 우리는 다음과 같이 표기한 뒤 모델링을 할 수 있다.

\[t_n = y_n + e_n\]

• \(t_n\) : (에러가 있는) 실제로 관측된 값
• \(y_n\) : (에러 free의) latent 값
• \(e_n\) : Gaussian Distribution에 따른 error term

\[P(t_n \mid y_n) = N(t_n \mid y_n, \beta^{-1})\]

위 식에서 \(\beta\)는 error term을 조절해주는 hyperparameter가 된다 ( variance / precision 결정 )

이를 matrix로 나타내면 다음과 같다.

\[P(T \mid Y) = N(T \mid Y, \beta^{-1}I_N)\]

그러면, 우리는 \(P(T)\)를 prior와 likelihood를 통해 다음과 같이 표기할 수 있게 된다.

\[P(T) = \int P(T\mid Y)P(Y)dY = \int N(T\mid Y, \beta^{-1}I_N)N(Y\mid 0,K)dY\]

( 위 식에서 \(P(T\mid Y)P(Y) = P(T,Y)\)를 앞으로 \(P(Z)\)라고 표현할 것이다. 이는 Multivariate Normal Distribution을 따른다 )

\(P(Z)\)에 log를 씌우면, 다음과 같이 된다.

\[\begin{align*} lnP(Z) &= lnP(Y) + lnP(T\mid Y)\\ &= -\frac{1}{2}(Y-0)^TK^{-1}(Y-0) -\frac{1}{2}(T-Y)^T\beta I_N(T-Y) + const \\ &= -\frac{1}{2}Y^TK^{-1}Y - -\frac{1}{2}(T-Y)^T \beta I_N(T-Y)+ const \end{align*}\]

위 식에서 second order term을 따지면, 다음과 같이 나타낼 수 있다.

\[-\frac{1}{2}Y^TK^{-1}Y - -\frac{\beta}{2}T^TT + \frac{\beta}{2}TY + \frac{\beta}{2}YT -\frac{\beta}{2}Y^TY\] \[=-\frac{1}{2}\begin{pmatrix} Y\\ T \end{pmatrix}^T \begin{pmatrix} K^{-1}+\beta I_N &-\beta I_N \\ -\beta I_N & \beta I_N \end{pmatrix} \begin{pmatrix} Y\\ T \end{pmatrix}\] \[=-\frac{1}{2}Z^T R Z\]

여기서, \(R\)는 \(Z\)의 Precision Matrix가 된다. 따라서, Covariance Matrix ( Precision Matrix의 역행렬 )은 다음과 같이 나오게 된다.

\[R^{-1} = \begin{pmatrix} K & K\\ K & (\beta I_N)^{-1}+K \end{pmatrix}\] \[P(Z) = N(Z \mid 0, R^{-1})\]

[복습] multivariate normal distribution의 marginal & conditional distribution

\[X = [X_1 \; \;X_2]^T\] \[\mu = [\mu_1 \; \; \mu_2]^T\] \[\sum = \begin{bmatrix} \sum_{11} & \sum_{12}\\ \sum_{21} & \sum_{22} \end{bmatrix}\]

marginal distribution과 conditional distribution은 각각 다음과 같다.

\[P(X_1) = N(X_1 \mid \mu,\sum_{11})\] \[P(X_1 \mid X_2)= N(X_1 \mid \mu_1 + \sum_{12}\sum_{22}^{-1}(X_2 - \mu_2), \sum_{11} - \sum_{12} \sum_{22}^{-1}\sum_{21})\]

이를 적용하여 \(P(T)\)를 구하면 다음과 같다.

\[P(T) = N(T \mid 0, (\beta I_N)^{-1} +K)\]

우리가 궁극적으로 구하고자 하는 것은, \(N\) 시점까지의 data가 있을 때, 그 다음 \(N+1\) 시점의 값을 예측하는 것이다!

\[P(t_{N+1} \mid T_N)\]

2) Mean and Covariance of \(P(t_{N+1} \mid T_N)\)

\(P(T) = N(T \mid 0, (\beta I_N)^{-1} +K)\) 라는 것은 앞에서 구했었다.

하지만 우리가 관심 있는것은 미래 (N+1) 시점의 값이다. 즉, \(P(t_{N+1} \mid T_N)\)에 관심이 있다.

\(P(t_{N+1} \mid T_N) = \frac{P(T_{N+1})}{P(T_N)}\) 이므로, 우리는 \(P(T_{N+1})\)을 구해야 한다.

\[P(T_{N+1}) = N(T \mid 0, cov)\]

여기서 \(cov\)는 다음과 같다.

\(cov = \begin{pmatrix} K_{11}+\beta & K_{12} & & & K_{1(N+1)}\\ K_{21} & K_{22}+\beta & & & K_{2(N+1)}\\ .... & & & & ...\\ K_{N1} & & & & K_{N(N+1)}\\ K_{(N+1)1} & & & K_{(N+1)N} & K_{(N+1)(N+1)}+\beta \end{pmatrix}\) = \(\bigl(\begin{smallmatrix} cov_N & k\\ k^T & c \end{smallmatrix}\bigr)\)

위에서 복습했듯, conditional distribution은 다음과 같다.

\[P(X_1 \mid X_2)= N(X_1 \mid \mu_1 + \sum_{12}\sum_{22}^{-1}(X_2 - \mu_2), \sum_{11} - \sum_{12} \sum_{22}^{-1}\sum_{21})\]

따라서 \(P(t_{N+1} \mid T_N)\)도 다음과 같이 나타낼 수 있다!

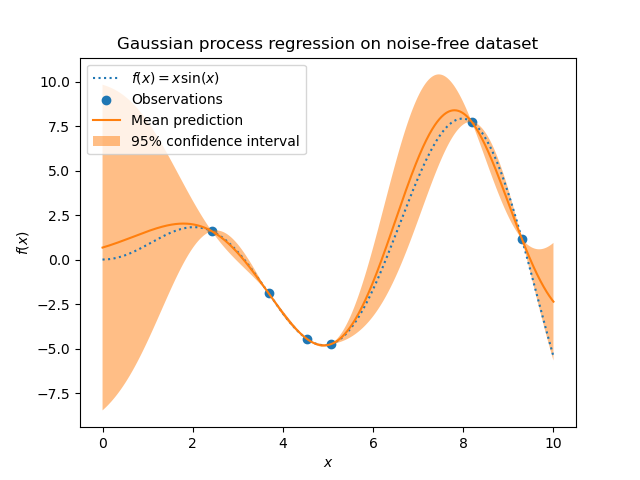
\[P(t_{N+1} \mid T_N) = N(t_{N+1} \mid 0 + k^T cov_N^{-1}(T_N-0), c-k^T cov_N^{-1}k)\]

지금까지 우리는 Gaussian Process를 이용하여 Regression을 했다.

특이한 점이 있다. 우리가 아는 regression에는 늘 weight(기울기)가 있었는데, 위에서는 보이지 않는 것 같다. 하지만 사실 이는 kernel function안에 모두 들어가있는 것이다! 여태까지는 regression을 하면 예측하는 값이 다 point estimation으로 딱 ‘특정값’으로 나왔었다. 하지만, 이제는 하나의 특정 값이 아닌 분포 (predictive distribution) \(P(t_{N+1} \mid T_N)\) 가 output으로 나오게 된다. 만약 그 예측 값을 딱 하나의 값으로 이야기해야 한다면, 그것은 우리가 구한 분포의 mean이 될 것이다.

https://scikit-learn.org/stable/_images/sphx_glr_plot_gpr_noisy_targets_002.png