On Embeddings for Numerical Features in Tabular Deep Learning (NeurIPS 2022)
https://openreview.net/pdf?id=pfI7u0eJAIr
Contents
- Abstract
Abstract
MLP = map scalar values of numerical features to high-dim embeddings
However … embeddings for numerical features are underexplored
Propose 2 different approaches to build embedding modules
- (1) Piecewise linear encoding
- (2) Periodic activations
\(\rightarrow\) Beneficial for many backbones
1. Introduction
Most previous works :
- focus on developing more powerful backbone
- overlook the design of embedding modules
This paper demonstrate that the embedding step has a substantial impact on the model effectiveness
Two different building blocks for constructing embeddings
- (1) Piecewise linear encoding
- (2) Periodic activation functions
2. Related Work
(1) Tabular DL
Do not consistently outperform GBDT models
Do not consistently outperform properly tuned simple models ( MLP, ResNet )
(2) Transformers in Tabular DL
Requires mapping the scalar values to high-dim vectors
Existing works: relatively simple computational blocks
- ex) FT-Transformer : use single linear layer
(3) Feature binning
Discretization technique
( numerical features \(\rightarrow\) categorical features )
(4) Periodic activations
key component in processing coordinate-like inputs
3. Embeddings for numerical features
Notation
Dataset : \(\left\{\left(x^j, y^j\right)\right\}_{j=1}^n\)
- \(y^j \in \mathbb{Y}\) represents the object’s label
- \(x^j=\left(x^{j(n u m)}, x^{j(c a t)}\right) \in \mathbb{X}\) .
(1) General Framework
“embeddings for numerical features”
- \(z_i=f_i\left(\left(x_i^{(\text {num })}\right) \in \mathbb{R}^{d_i}\right.\),
- where \(f_i(x)\) is the embedding function for the \(i\)-th numerical feature
- all features are computed independently of each other.
(2) Piecewise Linear encoding

\(\begin{aligned} & \operatorname{PLE}(x)=\left[e_1, \ldots, e_T\right] \in \mathbb{R}^T \\ & e_t= \begin{cases}0, & x<b_{t-1} \text { AND } t>1 \\ 1, & x \geq b_t \text { AND } t<T \\ \frac{x-b_{t-1}}{b_t-b_{t-1}}, & \text { otherwise }\end{cases} \end{aligned}\).
Note on attention-based models
Order-invariant … need positional information ( = feature index information )
\(\rightarrow\) place one linear layer after PLE ( = same effect as above )
\(f_i(x)=v_0+\sum_{t=1}^T e_t \cdot v_t=\operatorname{Linear}(\operatorname{PLE}(x))\).
a) Obtaining bins from quantiles
From empirical quantile
- \(b_t=\mathbf{Q}_{\frac{t}{T}}\left(\left\{x_i^{j(\text { num })}\right\}_{j \in J_{\text {train }}}\right)\).
b) Building target-aware bins
Supervised approach for constructing bins
-
recusrively splits its value range in a greedy manner using target as guidance
( = like decision tree )
(3) Periodic activation functions
Train the pre-activation coefficient ( instead of fixed )
\(f_i(x)=\operatorname{Periodic}(x)=\operatorname{concat}[\sin (v), \cos (v)], \quad v=\left[2 \pi c_1 x, \ldots, 2 \pi c_k x\right]\).
- where \(c_i\) are trainable parameters initialized from \(\mathcal{N}(0, \sigma)\).
- \(\sigma\) : important hyperparamter
- tune both \(\sigma\) and \(k\)
4. Experiments
(1) Datasets
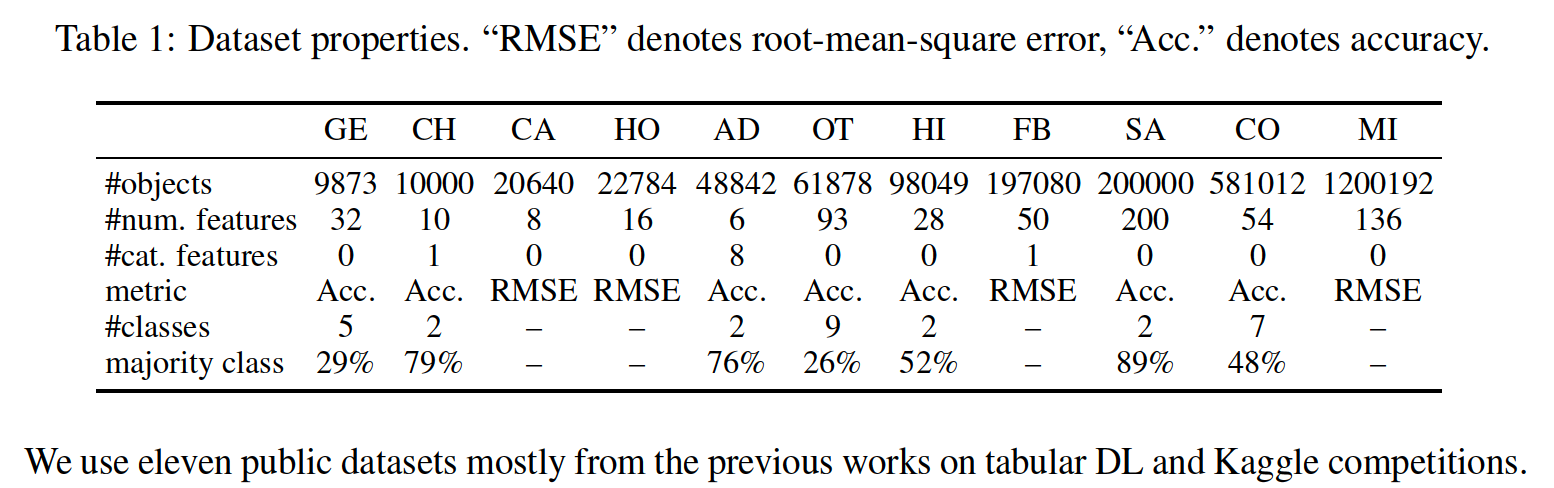
(2) Model Names

(3) Results
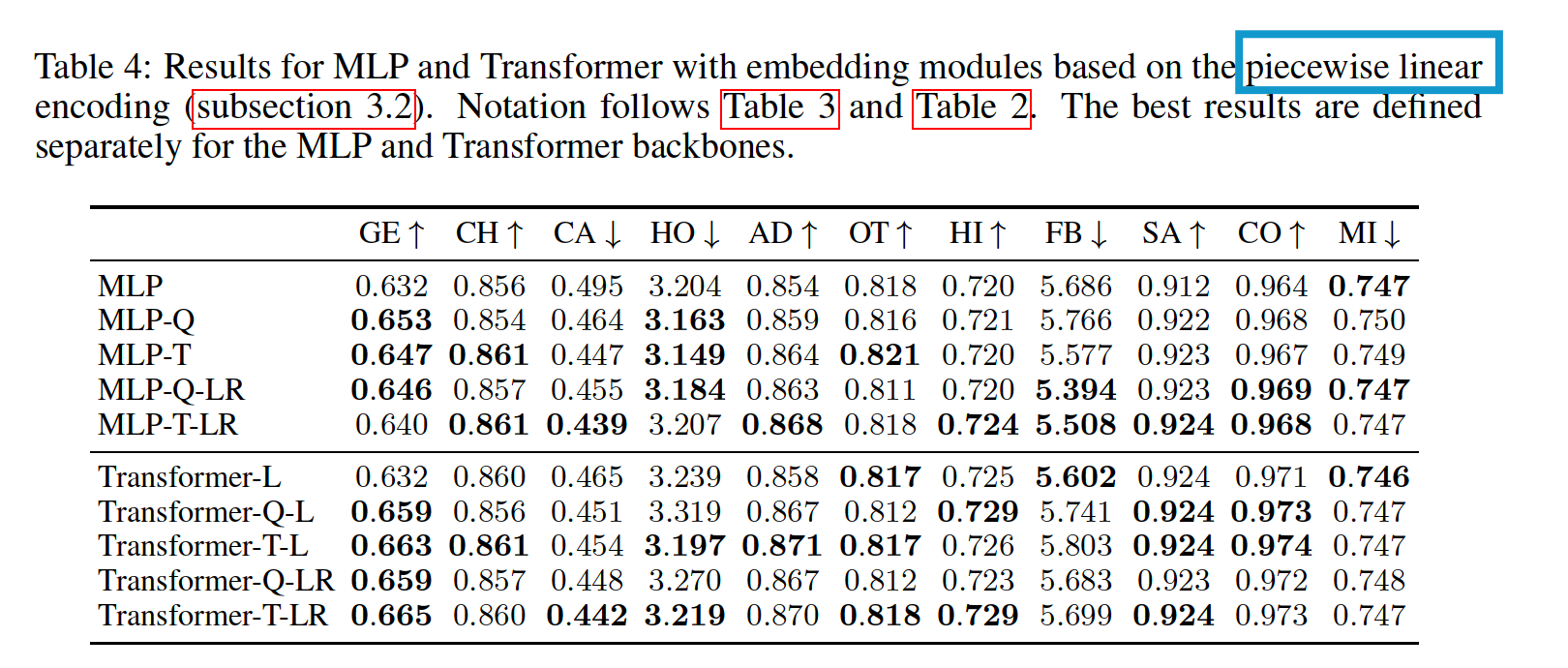
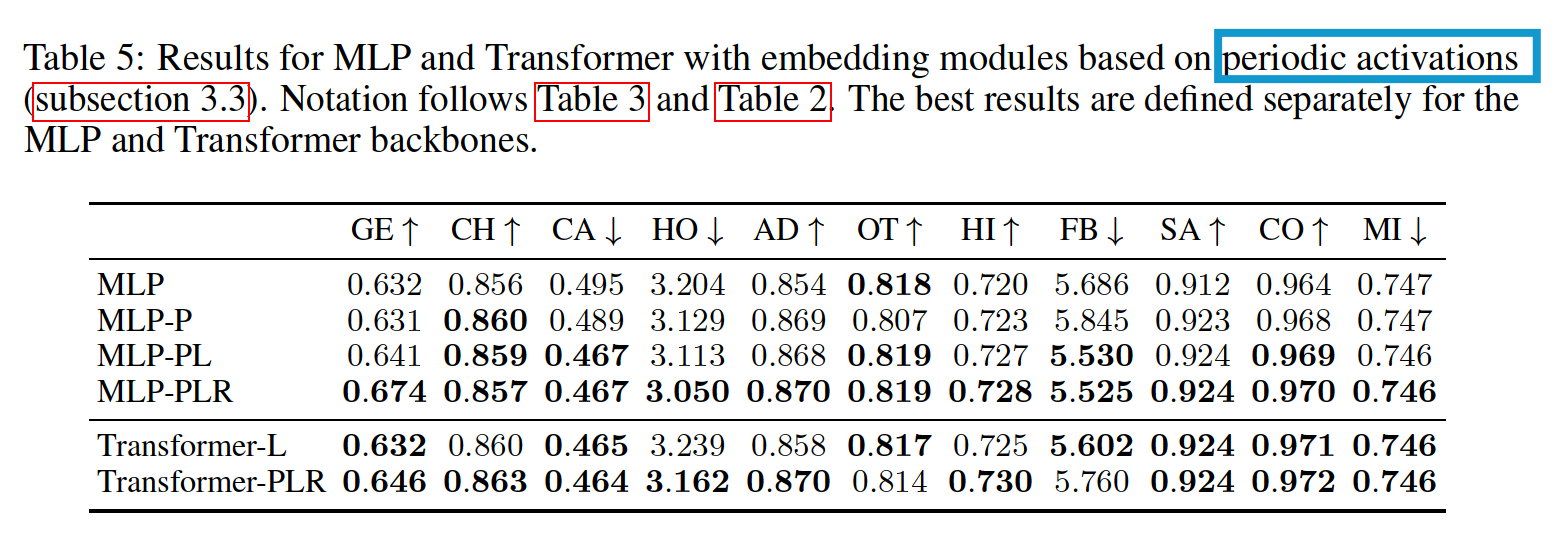
(4) DL vs. GBDT