VICReg : Variance-Invariance-Covariance Regularization for Self-Supervised Learning
Contents
- Abstract
- VICReg : Intuition
- VICReg : Detailed Description
- Method
0. Abstract
main challenge of SSL
- prevent a collapse in which the encoders produce constant or non-informative vectors
introduce VICReg (Variance-Invariance-Covariance Regularization)
-
explicitly avoids the collapse problem,
with two regularizations terms applied to both embeddings separately
- (1) a term that maintains the variance of each embedding dimension above a threshold
- (2) a term that decorrelates each pair of variables
-
does not require other techniques…
1. VICReg : Intuition
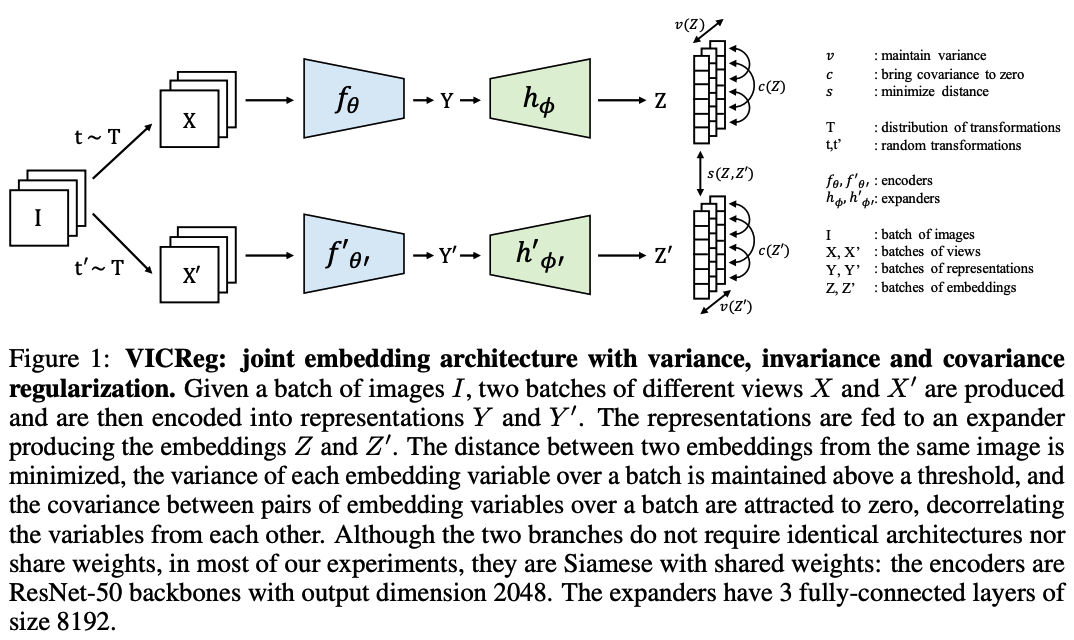
VICReg (Variance-Invariance-Covariance Regularization)
- a self-supervised method for training joint embedding architectures
- basic idea : use a loss function with three terms
- (1) Invariance :
- the MSE between the embedding vectors
- (2) Variance :
- a hinge loss to maintain the standard deviation (over a batch) of each variable
- forces the embedding vectors of samples within a batch to be different
- (3) Covariance :
- a term that attracts the covariances (over a batch) between every pair of (centered) embedding variables towards zero
- decorrelates the variables of each embedding
- prevents an informational collapse
- (1) Invariance :
2. VICReg : Detailed Description
use a Siamese net
- encoder : \(f_\theta\) ….. outputs representation
- expander : \(h_\phi\) ….. maps the representations into an embedding
- role 1 ) eliminate the information by which the two representations differ
- role 2 ) expand the dimension in a non-linear fashion so that decorrelating the embedding variables will reduce the dependencies between the variables of the representation vector.
- loss function : \(s\)
- learns invariance to data transformations
- regularized with a variance term \(v\) and a covariance term \(c\)
( After pretraining, the expander is discarded )
(1) Method
a) Notation
-
image \(i\) , from dataset \(\mathcal{D}\)
-
2 image transformations ( = random crops of the image, followed by color distortions )
- \(x=t(i)\).
- \(x^{\prime}=t^{\prime}(i)\).
-
2 representations
- \(y=f_\theta(x)\).
- \(y^{\prime}=f_\theta\left(x^{\prime}\right)\).
-
2 embeddings
- \(z=h_\phi(y)\).
- \(z^{\prime}=h_\phi\left(y^{\prime}\right)\).
\(\rightarrow\) Loss is computed on these embeddings
-
Batch of embeddings : \(Z^{\prime}=\left[z_1^{\prime}, \ldots, z_n^{\prime}\right]\).
- \(z^j\) : vector composed of each value at dimension \(j\) in all vectors in \(Z\)
b) variance, invariance and covariance terms
- Variance regularization term \(v\)
- a hinge function on the standard deviation of the embeddings along the batch dimension:
- \(v(Z)=\frac{1}{d} \sum_{j=1}^d \max \left(0, \gamma-S\left(z^j, \epsilon\right)\right)\).
- \(S(x, \epsilon)=\sqrt{\operatorname{Var}(x)+\epsilon},\).
- encourages the variance inside the current batch to be equal to \(\gamma\)
- prevent collapse with all inputs to be mapped to same vector
-
Covariance matrix of \(Z\)
-
\(C(Z)=\frac{1}{n-1} \sum_{i=1}^n\left(z_i-\bar{z}\right)\left(z_i-\bar{z}\right)^T, \quad \text { where } \quad \bar{z}=\frac{1}{n} \sum_{i=1}^n z_i\).
-
( inspired by Barlow Twins ) define covariance regularization as…
\(\rightarrow\) sum of the squared off-diagonal coefficients of \(C(Z)\)
\(\rightarrow\) \(c(Z)=\frac{1}{d} \sum_{i \neq j}[C(Z)]_{i, j}^2\).
-
- Invariance criterion \(s\) ( between \(Z\) and \(Z^{\prime}\) ) - MSE between each pair of vectors - \(s\left(Z, Z^{\prime}\right)=\frac{1}{n} \sum_i \mid \mid z_i-z_i^{\prime} \mid \mid _2^2\).
c) overall loss function
\(\ell\left(Z, Z^{\prime}\right)=\lambda s\left(Z, Z^{\prime}\right)+\mu\left[v(Z)+v\left(Z^{\prime}\right)\right]+\nu\left[c(Z)+c\left(Z^{\prime}\right)\right]\).
overall objective function ( over an unlabelled dataset \(\mathcal{D}\) )
- \(\mathcal{L}=\sum_{I \in \mathcal{D}} \sum_{t, t^{\prime} \sim \mathcal{T}} \ell\left(Z^I, Z^{\prime I}\right)\).
