[meta] (paper 8) Amortized Bayesian Meta-Learning

Amortized Bayesian Meta-Learning

Contents

1. Abstract
2. Introduction
3. Meta-learning with Hierarchical Variational Inference
4. Amortized Bayesian Meta-Learning
   1. Scaling Meta-Learning with Amortized VI
   2. Amortized VI using only Support Set
   3. Application Details
5. Algorithm 도식화

0. Abstract

Meta learning ( = Learning to Learning )

SOTA :

• 1) learning an “initialization”
• 2) optimization algorithm using training “episodes”

\(\rightarrow\) to learn “generalization ability”

한계점 : lack good QUANTIFICATION of UNCERTAINTY

제안 :

• efficiently amortizes “HVI” (Hierarchical Variational Inference) across tasks,
• learning prior over NN weights ( BBB 논문)

1. Introduction

Meta learning

• 목적 : perform well on “distribution of training TASKS”

• 상황 : new task, with SMALL training set

• 좋은 성능 뿐만 아니라, 좋은 “predictive uncertainty”를 가지는 것도 중요하다

  ( 주로 Bayesian 방법들이 이를 해결하곤 함 …. posterior over NN weight )

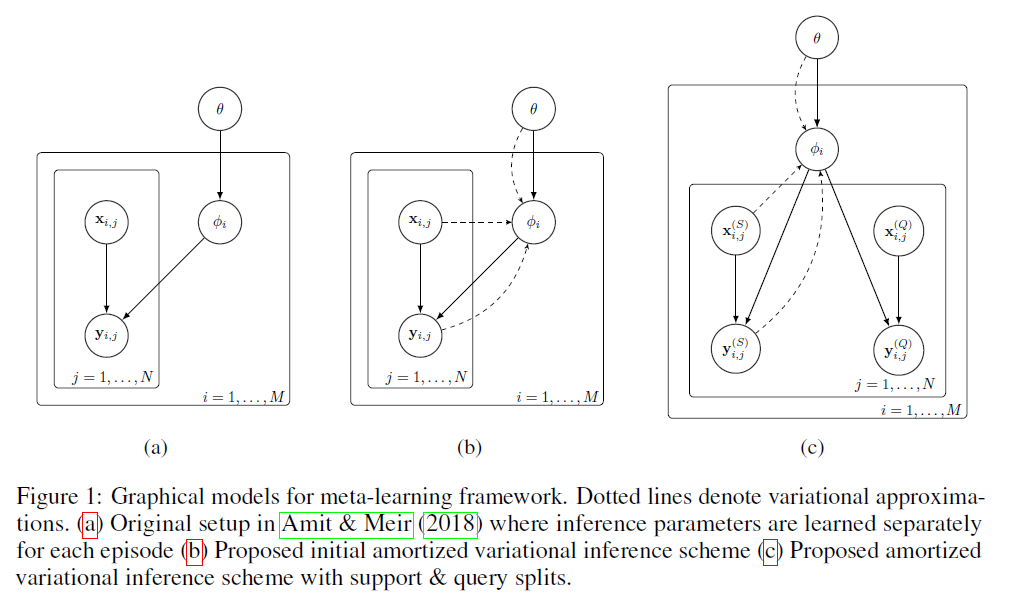
2. Meta-learning with Hierarchical Variational Inference

Hierarchical Variational Bayes 리뷰

( Amit & Meir (2018) … HVI를 meta-learning에 사용 )

Notation :

• \(M\) episode

• \(i^{th}\) episode의 데이터 = \(D_i\) ( 총 \(N\)개의 데이터 )

  ( \(\mathcal{D}_{i}=\left\{\left(\mathrm{x}_{i, j}, \mathbf{y}_{i, j}\right)\right\}_{j=1}^{N}\) )

• variable

  • global latent : \(\theta\)
  • episode-specific : \(\phi_{i}, i=1, \ldots M\)

• variational parameter

  • \(\psi\) : over global latent variable \(\theta\)
  • \(\lambda_{1}, \ldots, \lambda_{M}\) : over episode-specific variable : \(\phi_{i}, i=1, \ldots M\)

HVI의 ELBO

\(\begin{aligned} &\log \left[\prod_{i=1}^{M} p\left(\mathcal{D}_{i}\right)\right]=\log \left[\int p(\theta)\left[\prod_{i=1}^{M} \int p\left(\mathcal{D}_{i} \mid \phi_{i}\right) p\left(\phi_{i} \mid \theta\right) d \phi_{i}\right] d \theta\right] \\ &\geq \mathbb{E}_{q(\theta ; \psi)}\left[\log \left(\prod_{i=1}^{M} \int p\left(\mathcal{D}_{i} \mid \phi_{i}\right) p\left(\phi_{i} \mid \theta\right) d \phi_{i}\right)\right]-\operatorname{KL}(q(\theta ; \psi) \mid \mid p(\theta)) \\ &=\mathbb{E}_{q(\theta ; \psi)}\left[\sum_{i=1}^{M} \log \left(\int p\left(\mathcal{D}_{i} \mid \phi_{i}\right) p\left(\phi_{i} \mid \theta\right) d \phi_{i}\right)\right]-\operatorname{KL}(q(\theta ; \psi) \mid \mid p(\theta)) \\ &\geq \mathbb{E}_{q(\theta ; \psi)}\left[\sum_{i=1}^{M} \mathbb{E}_{q\left(\phi_{i} ; \lambda_{i}\right)}\left[\log p\left(\mathcal{D}_{i} \mid \phi_{i}\right)\right]-\operatorname{KL}\left(q\left(\phi_{i} ; \lambda_{i}\right) \mid \mid p\left(\phi_{i} \mid \theta\right)\right)\right]-\operatorname{KL}(q(\theta ; \psi) \mid \mid p(\theta)) \\ &=\mathcal{L}\left(\psi, \lambda_{1}, \ldots, \lambda_{M}\right) \end{aligned}\).

즉 , minimize negative ELBO

\(\begin{gathered} \underset{\psi, \lambda_{1} \ldots, \lambda_{M}}{\arg \max } \mathbb{E}_{q(\theta ; \psi)}\left[\sum_{i=1}^{M} \mathbb{E}_{q\left(\phi_{i} ; \lambda_{i}\right)}\left[\log p\left(\mathcal{D}_{i} \mid \phi_{i}\right)\right]-\operatorname{KL}\left(q\left(\phi_{i} ; \lambda_{i}\right) \mid \mid p\left(\phi_{i} \mid \theta\right)\right)\right]-\operatorname{KL}(q(\theta ; \psi) \mid \mid p(\theta)) \\ \equiv \underset{\psi, \lambda_{1} \ldots, \lambda_{M}}{\arg \min } \mathbb{E}_{q(\theta ; \psi)}\left[\sum_{i=1}^{M}-\mathbb{E}_{q\left(\phi_{i} ; \lambda_{i}\right)}\left[\log p\left(\mathcal{D}_{i} \mid \phi_{i}\right)\right]+\operatorname{KL}\left(q\left(\phi_{i} ; \lambda_{i}\right) \mid \mid p\left(\phi_{i} \mid \theta\right)\right)\right]+\operatorname{KL}(q(\theta ; \psi) \mid \mid p(\theta)) \end{gathered}\).

Amit & Meir(2018)는 이를 모든 variational parameter에 대해 mini-batch GD를 수행함.

3. Amortized Bayesian Meta-Learning

3-1. Scaling Meta-Learning with Amortized VI

[ Notation 복습 ]

variational param \(\lambda_{1}, \ldots, \lambda_{M}\) : over episode-specific variable : \(\phi_{i}, i=1, \ldots M\)

[ 문제점 ]

local variational parameter \(\lambda_i\)를 모든 episode \(M\)에 대해서 다 계싼하는 거는 너무 HEAVY!

( 더군다나, \(\phi_i\) 가 “DNN”의 weight고, \(\lambda_i\)가 이 weight distribution의 variational parameter일 경우! )

[ 해결책 ]

\(M\) different variational parameters \(\lambda_i\) 대신, AVI (Amortized Variational Inference) 사용하자!

\(\rightarrow\) global learned model is used to predict \(\lambda_i\) from \(\mathcal{D}_i\)

ex) VAE

[ 새로운 Notation 소개 ]

\(\mathcal{L}_{\mathcal{D}_{i}}(\lambda, \theta)=-\mathbb{E}_{q\left(\phi_{i} ; \lambda\right)}\left[\log p\left(\mathcal{D}_{i} \mid \phi_{i}\right)\right]+\mathrm{KL}\left(q\left(\phi_{i} ; \lambda\right) \mid \mid p\left(\phi_{i} \mid \theta\right)\right)\).

• data \(\mathcal{D_i}\)에 해당하는 loss function 부분

\(S G D_{K}\left(\mathcal{D}, \lambda^{(\text {init })}, \theta\right)\).

• \(K\) step의 SGD 이후의 variational parameter

• 상세 과정 :

  • step 1) \(\lambda^{(0)}=\lambda^{(\text {init })}\)

  • step 2) for \(k=0, \ldots, K-1\), set

    \(\lambda^{(k+1)}=\lambda^{(k)}-\alpha \nabla_{\lambda^{(k)}} \mathcal{L}_{\mathcal{D}}\left(\lambda^{(k)}, \theta\right)\).

Variational distribution for each dataset \(q_{\theta}\left(\phi_{i} \mid D_{i}\right)\) in terms of \(S G D_{K}\left(\mathcal{D}, \lambda^{(\text {init })}, \theta\right)\)

• \(q_{\theta}\left(\phi_{i} \mid \mathcal{D}_{i}\right)=q\left(\phi_{i} ; S G D_{K}\left(\mathcal{D}_{i}, \theta, \theta\right)\right)\).
• 위 식에서 \(\theta\)의 2가지 역할
  • 1) global INITIALIZATION of local VARIATIONAL parameters
  • 2) parameters of the prior \(p(\phi \mid \theta)\)

[ Simplification ]

( 우선, 우리의 상황 : \(M >>N\) )

• Uncertainty in global latent variables \(\theta\) : LOW ( \(M\)이 크니까)
• 따라서, \(\theta\)에 대해서는 “point estimate”를 사용할 것!
• 즉, let \(q(\theta ; \psi)\) be a direct delta function
• 따라서, global variational parameter \(\psi\)가 필요 없어짐

[ negative ELBO ]

위와 같은 AVI 가정 하에서의 negative ELBO 변화 :

• (기존) \(\underset{\psi, \lambda_{1} \ldots, \lambda_{M}}{\arg \min } \mathbb{E}_{q(\theta ; \psi)}\left[\sum_{i=1}^{M}-\mathbb{E}_{q\left(\phi_{i} ; \lambda_{i}\right)}\left[\log p\left(\mathcal{D}_{i} \mid \phi_{i}\right)\right]+\operatorname{KL}\left(q\left(\phi_{i} ; \lambda_{i}\right) \mid \mid p\left(\phi_{i} \mid \theta\right)\right)\right]+\operatorname{KL}(q(\theta ; \psi) \mid \mid p(\theta))\).
• (AVI) \(\underset{\psi}{\arg \min } \mathbb{E}_{q(\theta ; \psi)}\left[\sum_{i=1}^{M}-\mathbb{E}_{q_{\theta}\left(\phi_{i} \mid \mathcal{D}_{i}\right)}\left[\log p\left(\mathcal{D}_{i} \mid \phi_{i}\right)\right]+\operatorname{KL}\left(q_{\theta}\left(\phi_{i} \mid \mathcal{D}_{i}\right) \mid \mid p\left(\phi_{i} \mid \theta\right)\right)\right]+\operatorname{KL}(q(\theta ; \psi) \mid \mid p(\theta))\).
• (AVI + Simplification) \(\underset{\theta}{\arg \min }\left[\sum_{i=1}^{M}-\mathbb{E}_{q_{\theta}\left(\phi_{i} \mid \mathcal{D}_{i}\right)}\left[\log p\left(\mathcal{D}_{i} \mid \phi_{i}\right)\right]+\operatorname{KL}\left(q_{\theta}\left(\phi_{i} \mid \mathcal{D}_{i}\right) \mid \mid p\left(\phi_{i} \mid \theta\right)\right)\right]+\operatorname{KL}(q(\theta) \mid \mid p(\theta))\).

3-2. Amortized VI using only Support Set

[ Notation ]

\(\mathcal{D}_{i}=\mathcal{D}_{i}^{(S)} \cup \mathcal{D}_{i}^{(Q)}\).

, where \(\mathcal{D}_{i}^{(S)}=\left\{\left(\mathbf{x}_{i, j}^{(S)}, \mathbf{y}_{i, j}^{(S)}\right)\right\}_{j=1}^{N}\) and \(\mathcal{D}_{i}^{(Q)}=\left\{\left(\mathbf{x}_{i, j}^{(Q)}, \mathbf{y}_{i, j}^{(Q)}\right)\right\}_{j=1}^{N^{\prime}}\)

\(\mathcal{D}_{i}\) 가 아닌 \(\mathcal{D}_{i}^{(S)}\) 만이 주어진 상황을 가정!

그런 뒤, performance of model은 \(\mathcal{D}_{i}^{(Q)}\)에 대해서 계산!

[ 최종 Loss Function ]

\(\underset{\theta}{\arg \min }\left[\sum_{i=1}^{M}-\mathbb{E}_{q_{\theta}\left(\phi_{i} \mid \mathcal{D}_{i}^{(S)}\right)}\left[\log p\left(\mathcal{D}_{i} \mid \phi_{i}\right)\right]+\mathrm{KL}\left(q_{\theta}\left(\phi_{i} \mid \mathcal{D}_{i}^{(S)}\right) \mid \mid p\left(\phi_{i} \mid \theta\right)\right)\right]+\operatorname{KL}(q(\theta) \mid \mid p(\theta))\)>

3-3. Application Details

“Fully Factorized Gaussian distribution” 가정

• let \(\theta=\left\{\mu_{\theta}, \sigma_{\theta}^{2}\right\}\), where \(\mu_{\theta} \in \mathbb{R}^{D}\) and \(\sigma_{\theta}^{2} \in \mathbb{R}^{D}\)

(1) Model (likelihood) :

• \(p\left(\phi_{i} \mid \theta\right)=\mathcal{N}\left(\phi_{i} ; \boldsymbol{\mu}_{\boldsymbol{\theta}}, \boldsymbol{\sigma}_{\boldsymbol{\theta}}^{2} \mathbf{I}\right)\).

(2) Variational Distribution :

• \(\begin{aligned} &\left\{\mu_{\lambda}^{(\boldsymbol{K})},{\sigma^{2}}_{\boldsymbol{\lambda}}^{(\boldsymbol{K})}\right\}=S G D_{K}\left(\mathcal{D}_{i}^{(S)}, \theta, \theta\right) \\ &q_{\theta}\left(\phi_{i} \mid \mathcal{D}_{i}^{(S)}\right)=\mathcal{N}\left(\phi_{i} ; \boldsymbol{\mu}_{\boldsymbol{\lambda}}^{(\boldsymbol{K})},{\boldsymbol{\sigma}}_{\boldsymbol{\lambda}}^{2(\boldsymbol{K})}\right) \end{aligned}\).

(3) Prior :

• \(p(\theta)=\mathcal{N}(\boldsymbol{\mu} ; \mathbf{0}, \mathbf{I}) \cdot \prod_{l=1}^{D} \operatorname{Gamma}\left(\tau_{l} ; a_{0}, b_{0}\right)\).

4. Algorithm 도식화