(Deep Bayes) 04.EM Algorithm

[Deep Bayes] 04. EM Algorithm

해당 내용은 https://deepbayes.ru/ (Deep Bayes 강의)를 듣고 정리한 내용이다.

1. Introduction

이번 포스트에서는, (1) Variational Lower Bound와, 이를 활용한 알고리즘인 (2) EM Algorithm에 대해 알아볼 것이다. EM algorithm의 E-step과 M-step이 각각 어떻게 이루어지는지 알아보자.

복습

\(log\;p(X \mid \theta)\) 는 다음과 같이 ELBO 와 KL-Divergence 두 부분으로 나눌 수 있었다.

\[log\;p(X\mid \theta) = \int q(Z)\; log \frac{p(X,Z\mid \theta)}{q(Z)}dZ + \int q(Z)log\frac{q(Z)}{p(Z\mid X,\theta)}dZ\]

위 식의 우변의 오른쪽 부분은 KL-Divergence로, 항상 non-negative하기 때문에 우리는 위 식을 다음과 같이 표현할 수 있다.

\[log\;p(X\mid \theta) =L(q,\theta) + KL(q\mid \mid p) \geq L(q,\theta)\]

따라서 우리는 ELBO를 최대화해야 한다.

2. Variational Lower Bound

함수 \(g(\xi,x)\)가 다음 조건을 만족할 경우, 우리는 이를 함수 \(f(x)\)에 대한 variational lower bound라고 한다.

• 조건 1) 모든 \(\xi\)에 대해, \(f(x) \geq g(\xi, x)를 만족한다\)
• 조건 2) \(f(x_0) = g(\xi(x_0),x_0)\) 를 만족시키는 \(\xi(x_0)\) 가 존재한다.

만약 우리가 \(f(x)\)에 대한 variational lower bound \(g(\xi, x)\) 를 찾으면, 우리는 \(f(x)\)를 최대화 하는 문제를 다음과 같은 문제로 바꿔서 풀 수 있다.

반복적으로 (iteratively) 아래의 두 update 과정을 반복한다

• \(x_n = \underset{x}{argmax}\;g(\xi_{n-1},x)\) —————————— (a)
• \(\xi_n = \xi(x_n) = \underset{\xi}{argmax}\;g(\xi, x_n)\) ——————— (b)

직관적으로 생각해보자. 우리가 어떤 A를 최대화 해야하는 문제에 직면해있다. 그리고 우리는 A의 lower bound가 B라는 것을 알 수 있다. 이를 푸는 방법으로, A를 직접적으로 최대화 하는 방법도 있지만, B를 최대한 크게 만들 수도 있다. B를 최대한 크게 만들기 위해, 우선 lower bound B에서 가장 큰 값을 가지는 \(x\)값을 찾는다 (위 설명의 (a) 단계). 그리고 해당 \(x\)값을 찾은 뒤, 해당 \(x\)값에서 B가 가장 커지도록 B의 parameter를 조정한다. (위 설명의 (b) 단계) . 이 (a), (b) 단계를 서로 반복적으로 시행하다보면 (iteratively), 이는 곧 A를 최대화하는 것과 같게 될 것이다.

이러한 idea를 적용한 것이 바로 EM Algorithm이다.

3. EM Algorithm

다시 원래 문제로 돌아오자. 우리는 lower bound인 \(L(q,\theta)\)를 최대화 해야 한다.

\[L(q,\theta) = \int q(Z)\; log \frac{p(X,Z\mid \theta)}{q(Z)}dZ\]

그러기 위해서 다음과 같은 과정을 반복한다.

E-step ( Expectation step)

• 모수 \(\theta\)를 고정 시켜 놓은 채, Lower Bound ( \(L(q,\theta)\) )를 최대화하는 \(q\)를 구한다.
• updating equation : \(q(Z) = \underset{q}{argmax}\;L(q,\theta_0) = \underset{q}{argmin}KL(q\mid \mid p) = p(Z \mid X,\theta_0)\)
• 이 단계가 ‘Expectation’ step으로 불리는 이유는, \(\theta_0\)가 주어 졌을 때의 \(q\)값의 기댓값을 구하기 때문이다.

M-step ( Maximization Step )

• \(q\)를 고정 시켜 놓은 채, Lower Bound ( \(L(q,\theta)\) )를 최대화하는 \(\theta\)를 구한다.
• updating equation : \(\theta_{*} = \underset{\theta}{argmax}L(q,\theta) = \underset{\theta}{argmax}E_z logp(X,Z \mid \theta)\)
• 이 단계가 ‘Maximization’ step으로 불리는 이유는, 우리가 궁극적으로 구하고자 하는 \(\theta\)를 구하기 위해 Lower Bound를 maximize하기 때문이다.

아래 그림을 통해 쉽게 이해할 수 있을 것이다.

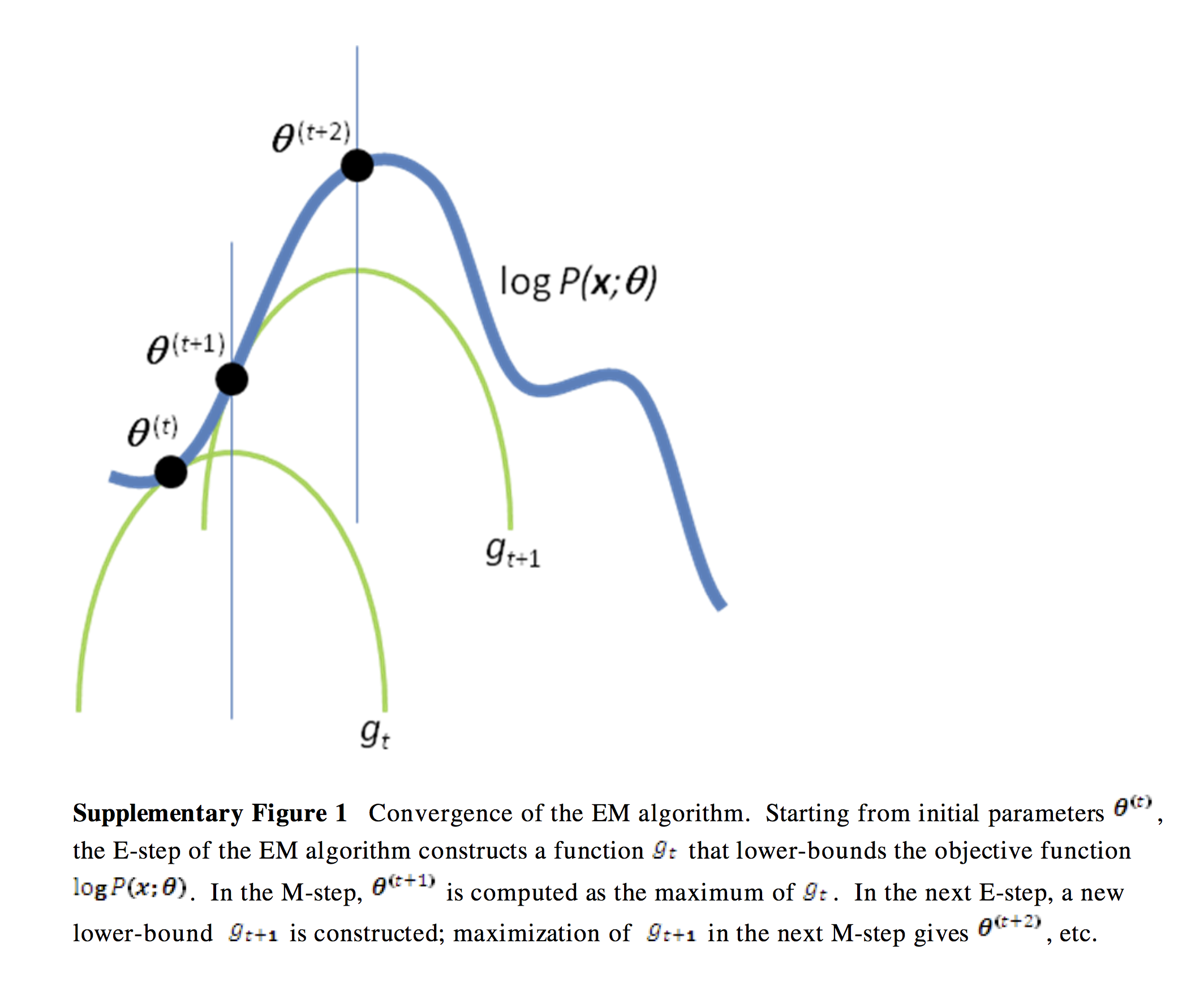
( https://people.duke.edu/~ccc14/sta-663/_images/EMAlgorithm_19_0.png )

저 그림에서 파란색 그래프가 우리가 알고 싶어하는 \(log\; p(x \mid \theta)\)이다. 이를 최대화하기 위해, 우리는 초록색 그래프인 lower bound \(L(q,\theta)\) 를 최대한 파란색 그래프와 밀착하게 닿도록 끌어올린다. 이 과정을 위의 E-step과 M-step을 iterative하게 반복함으로서 이루어낼 수 있는 것이다.

EM Algorithm의 장점

• 1 ) 대부분의 경우에 있어서, E-step 과 M-step은 closed form으로 풀 수 있다
• 2 ) 간단한 distribution의 mixture를 통해 보다 복잡한 모델을 만들 수 있다
• 3 ) true posterior \(p(Z\mid X,\theta)\) 가 다루기 쉽지 않을 때, 이를 근사하는 다루기 쉬운 \(q(Z)\)를 찾아서 이 문제를 풀 수 있다 ( optimization problem으로 변환 )
• 4 ) missing data를 잠재 변수(latent variable)로 취급함으로써 문제를 해결할 수 있다

예전에 EM Algorithm에 대해 영어로 쓴 포스트도 있다. 이를 추가로 참고해봐도 좋을 것 같다. ( https://seunghan96.github.io/stat/10.-em-EM_algorithm(2)/ )