(paper) Probabilistic Time Series Forecasting with Structured Shape and Temporal Diversity

Probabilistic Time Series Forecasting with Structured Shape and Temporal Diversity (2020)

Contents

1. Abstract
2. Introduction
3. Related Work
   1. Probabilistic Forecasting
   2. Diverse Predictions
4. Shape and Time diversity for probabilistic time series forecasting
   1. STRIPE diversity module based on determinantal point processes
   2. STRIPE learning and sequential shape and temporal diversity sampling

0. Abstract

Introduce STRIPE

• address the problem for non-stationary time series
• model for representing “structured diversity”, based on
  • 1) shape
  • 2) time features
• agnostic to the forecasting model
• diversification mechanism, relying on DPP(Determinantal Point Processes)

Introduce 2 DPP kernels…for modeling diverse trajectories in terms of..

• 1) shape
• 2) time

1. Introduction

DETERMINISTIC \(\rightarrow\) limits single trajectory prediction, without uncertainty quantification

PROBABILISTIC \(\rightarrow\) enable to sample diverse predictions from a given input

• ex) deterministic methods, that predict the quantiles of predictive distn
• ex) probabilistic methods, that sample future values from approximate distn
• ex) implicitly with latent generative models

Introduce a model for including Shape and Time diveRsIty in Probabilistic forEcasting (STRIPE)

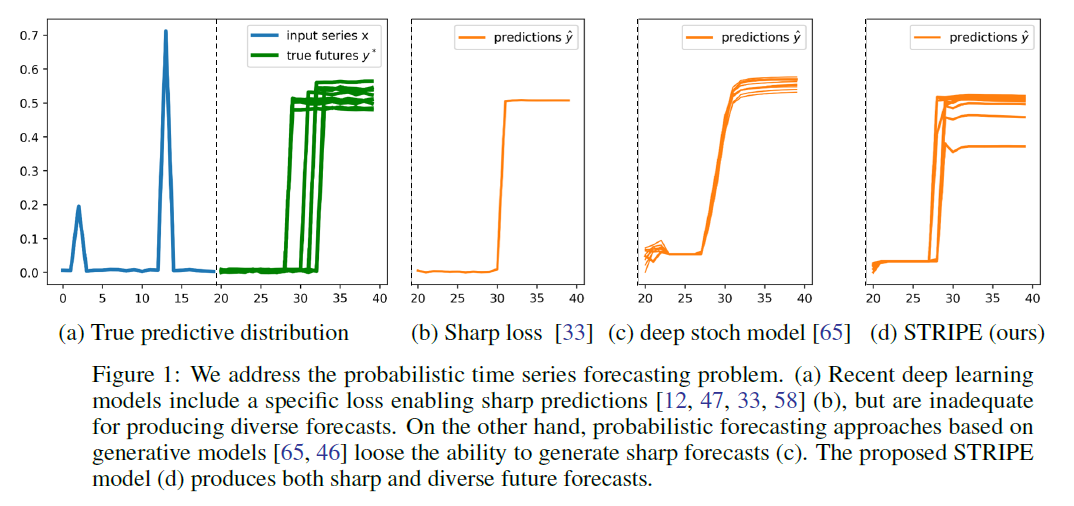
• STRIPE : enables to produce sharp & diverse forecasts

2. Related Work

(1) Probabilistic Forecasting

2 Types

• 1) deterministic methods
  • add variance estimation with MCDO
  • predict the quantiles of this distn
• 2) probabilistic methods : approximate the predictive distn
  • explicitly with a parametric distn ( ex. Gaussian for DeepAR )
  • implicitly with a generative model with latent variables ( ex. cVAE, cGANs, NF )

\(\rightarrow\) lack the ability to produce SHARP forecasts, by minimizing variants of MSE

(2) Diverse Predictions

to improve diversity of predictions, several repulsive schemes

ex) DPP (Determinantal Point Processes)

• enforce structured diversity, via the choice of positive semi-definite kernel
• ex) document sumamrization, rec sys, object detection

ex) GDPP

• based on matching generated & true sample diversity, by aligning the corresponding DPP kernels
• limits their use in datasets, where full distn of possible outcomes is accessible

\(\leftrightarrow\) our approach is applicable in realistic scenarii, where only a single label is available for each training sample

3. Shape and Time diversity for probabilistic time series forecasting

STRIPE model

• include shape & time diversity
• notation
  • input sequence : \(\mathrm{x}_{1: T}=\left(\mathrm{x}_{1}, \ldots, \mathrm{x}_{T}\right) \in \mathbb{R}^{p \times T}\)
  • goal : sample a set of \(N\) diverse and plausible future trajectories \(\hat{\mathbf{y}}^{(i)}=\left(\hat{\mathbf{y}}_{T+1}, \ldots, \hat{\mathbf{y}}_{T+\tau}\right) \in \mathbb{R}^{d \times \tau}\) from the data future distribution \(\hat{\mathbf{y}}^{(i)} \sim p\left(. \mid \mathbf{x}_{1: T}\right)\)
• builds upon a general seq2seq
• agnostic to specific choice of forecasting model
  • 1) can be deterministic RNN
  • 2) can be probabilistic conditional generative model ( cVAE, cGAN, NF )

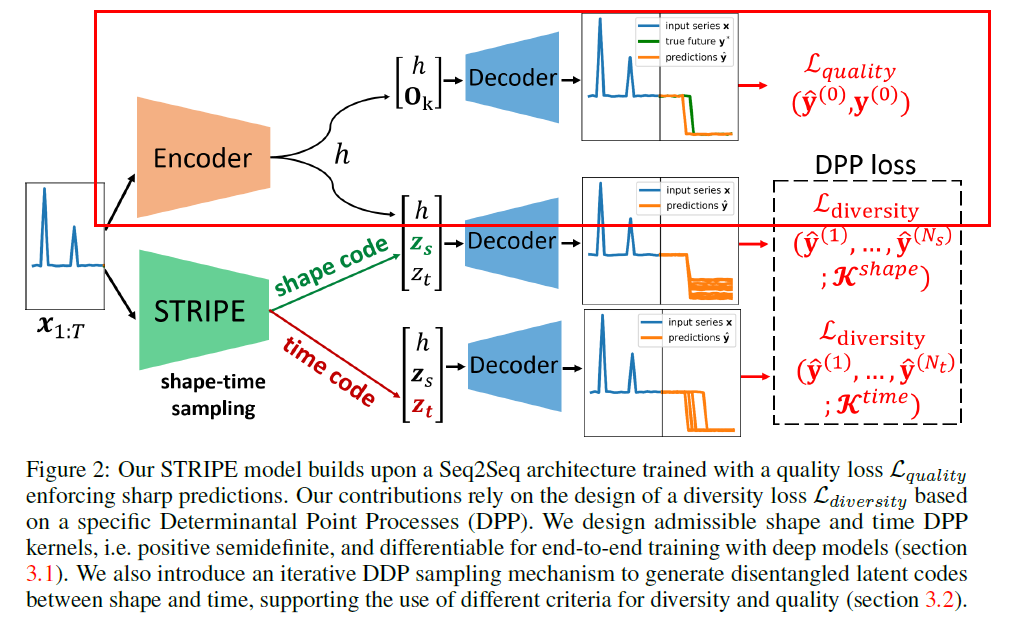
[ Train the Predictor ]

• concatenate \(h\) with a vector \(\mathbf{0}_{k} \in \mathbb{R}^{k}\)

  (free space left for the diversifying variables)

• decoder produces a forecasted trajectory \(\hat{\mathbf{y}}^{(0)}=\) \(\left(\hat{\mathbf{y}}_{T+1}^{(0)}, \ldots, \hat{\mathbf{y}}_{T+\tau}^{(0)}\right)\)

• predictor minimizes a quality loss \(\mathcal{L}_{\text {quality }}\left(\hat{\mathbf{y}}^{(0)}, \mathbf{y}^{(0)}\right)\)

  • \(\mathcal{L}_{\text {quality }}\) : based on DILATE loss

    ( = enforce sharp predictions, with accurate temporal localization )

[ for Structured Diversity ]

• concatenate \(h\) with diversifying latent variables \(z \in \mathbb{R}^{k}\)
• produce \(N\) future trajectories \(\left\{\hat{\mathbf{y}}^{(i)}\right\}_{i=1, \ldots, N}\) ( \(N\) : MTS )
• augment \(\mathcal{L}_{\text {quality }}(\cdot)\) with a diversification loss \(\mathcal{L}_{\text {diversity }}(\cdot ; \mathcal{K})\)

\(\mathcal{L}_{\text {STRIPE }}\left(\hat{\mathbf{y}}^{(0)}, \ldots, \hat{\mathbf{y}}^{(N)}, \mathbf{y}^{(0)} ; \mathcal{K}\right)=\mathcal{L}_{\text {quality }}\left(\hat{\mathbf{y}}^{(0)}, \mathbf{y}^{(0)}\right)+\lambda \mathcal{L}_{\text {diversity }}\left(\hat{\mathbf{y}}^{(1)}, \ldots, \hat{\mathbf{y}}^{(N)} ; \mathcal{K}\right)\).

(1) STRIPE diversity module based on determinantal point processes

\(\mathcal{L}_{\text {diversity}}\).

• relies on determinantal point processes (DPP)
• convenient probabilistic tool for enforcing structured diversity via adequately chosen positive semi-definite kernels

For comparing two time series \(\mathbf{y}_{1}\) and \(\mathbf{y}_{2}\)….

• introduce the two following kernels \(\mathcal{K}^{\text {shape }}\) and \(\mathcal{K}^{\text {time }}\)

\(\begin{aligned} &\mathcal{K}^{\text {shape }}\left(\mathrm{y}_{1}, \mathrm{y}_{2}\right)=e^{-\gamma \mathrm{DTW}_{\gamma}\left(\mathbf{y}_{1}, \mathrm{y}_{2}\right)} \\ &\mathcal{K}^{t i m e}\left(\mathrm{y}_{1}, \mathrm{y}_{2}\right)=\operatorname{TDI}_{\gamma}\left(\mathrm{y}_{1}, \mathrm{y}_{2}\right)=\frac{1}{Z} \sum_{\mathbf{A} \in \mathcal{A}_{\tau, \tau}}\langle\mathbf{A}, \Omega\rangle \exp ^{-\frac{\left\langle\mathbf{A}, \Delta\left(\mathrm{y}_{1}, \mathrm{y}_{2}\right)\right\rangle}{\gamma}} \end{aligned}\).

• where DTW \(_{\gamma}\left(\mathrm{y}_{1}, \mathrm{y}_{2}\right):=-\gamma \log \left(\sum_{\mathrm{A} \in \mathcal{A}_{\tau, \tau}} \exp ^{-\frac{\left\langle\mathbf{A}, \boldsymbol{\Delta}\left(\mathrm{y}_{1}, \mathrm{y}_{2}\right)\right\rangle}{\gamma}}\right)\) is a smooth relaxation of Dy-

DPP diversity loss

• combine 2 differentiable PSD kernels
• \(\mathcal{L}_{\text {diversity }}(\mathcal{Y} ; \mathbf{K})=-\mathbb{E}_{Y \sim D P P(\mathbf{K})}\mid Y\mid =-\operatorname{Trace}\left(\mathbf{I}-(\mathbf{K}+\mathbf{I})^{-1}\right)\).

(2) STRIPE learning and sequential shape and temporal diversity sampling

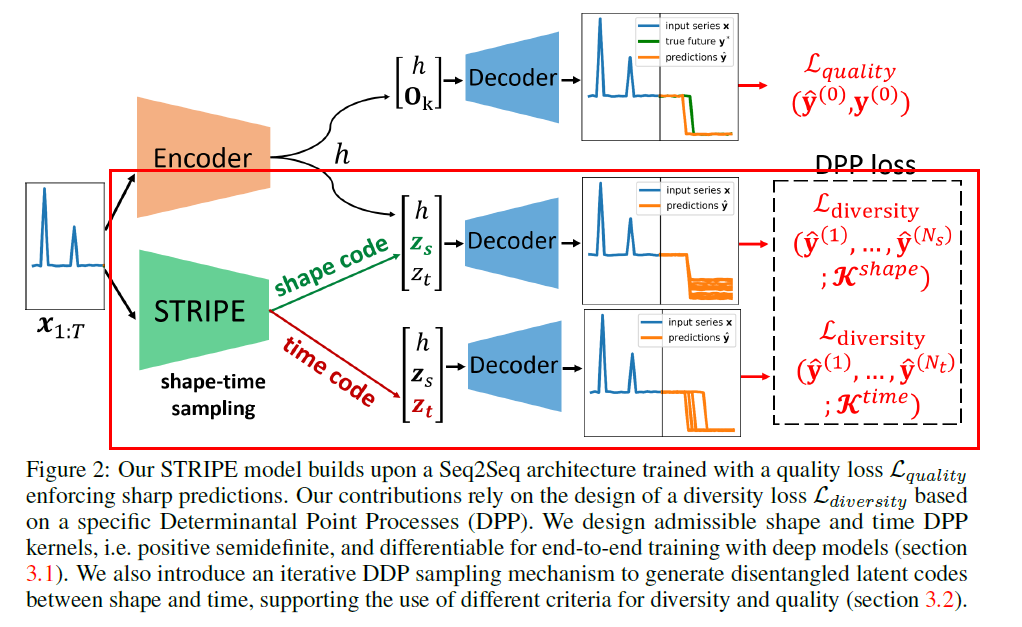
• propose a sequential (1) shape and (2) temporal diversity sampling scheme,

  which enables to jointly model variations in shape and time without altering prediction quality

• independently training two proposal modules ..
  • 1) STRIPE-shape
  • 2) STRIPE-time
• complement the latent state \(h\) of the forecaster with a diversifying latent variable \(z \in \mathbb{R}^{k}\)
• \(z=\left(z_{s}, z_{t}\right) \in \mathbb{R}^{k}\).
  • decomposed into shape \(z_{s} \in \mathbb{R}^{k / 2}\) and temporal \(z_{t} \in \mathbb{R}^{k / 2}\) components

• [STRIPE-shape]

  • decoder takes the concatenated state \(\left(h, z_{s}^{(i)}, z_{t}\right)\) for a fixed \(z_{t}\) and produces \(N_{s}\) future trajectories \(\hat{\mathbf{y}}^{(i)}\),

    whose diversity is maximized with \(\mathcal{L}_{\text {diversity }}\left(\hat{\mathbf{y}}^{(1)}, \ldots, \hat{\mathbf{y}}^{\left(N_{s}\right)} ; \mathbf{K}^{\text {shape }}\right)\)

• [STRIPE-time]

  • vise versa

Sequential Sampling at test time

sequentially maximizing …

• the SHAPE diversity with STRIPE-shape
• the TEMPORAL diversity of each shape with STRIPE-time

ordering of shape+time is actually important,

since the notion of time diversity between two time series is only meaningful, if they have a similar shape