Generative Learning for Financial TS with Irregular and Scale-Invariant Patterns

Generative Learning for Financial TS with Irregular and Scale-Invariant Patterns

Contents

1. Abstract
2. Introduction
3. Related Work
4. Problem Statement
5. FTS-DIffusion Framwork
   1. Pattern Recognition
   2. Pattern Generation
   3. Pattern Evolution

Abstract

Limited data in financial applications

\(\rightarrow\) Synthesize financial TS !!

• Challenges: Irregular & Scale-invariant patterns

( Existing approaches: assume regularity & uniformity )

FTS-Diffusion

To model Irregular & Scale-invariant patterns that consists of 3 modules

• (1. Patterrn Recognition) Scale-invariant pattern recogntion algorithm
  • to extract recurring patterns that vary in duration & magnitude
• (2. Pattern Generation) Diffusion-based generative network
  • to synthesize segments of patterns
• (3. Pattern Evolution)
  • model the temporal transition of patterns

1. Introduction

Problem in Finance data

• (1) dearth of data & low signal-to-noise ratio
• (2) cannot run experiments to obtain more data

Solution: Data Augmentation, using diffusion model

Still, challenge in “finance TS” … Why??

\(\rightarrow\) Two reasons:

• (1) Lack of regularity
• (2) Scale-invariance
  • financial TS appear to conatin more subtle patterns that repeat themselves with varyring duration and magnitude

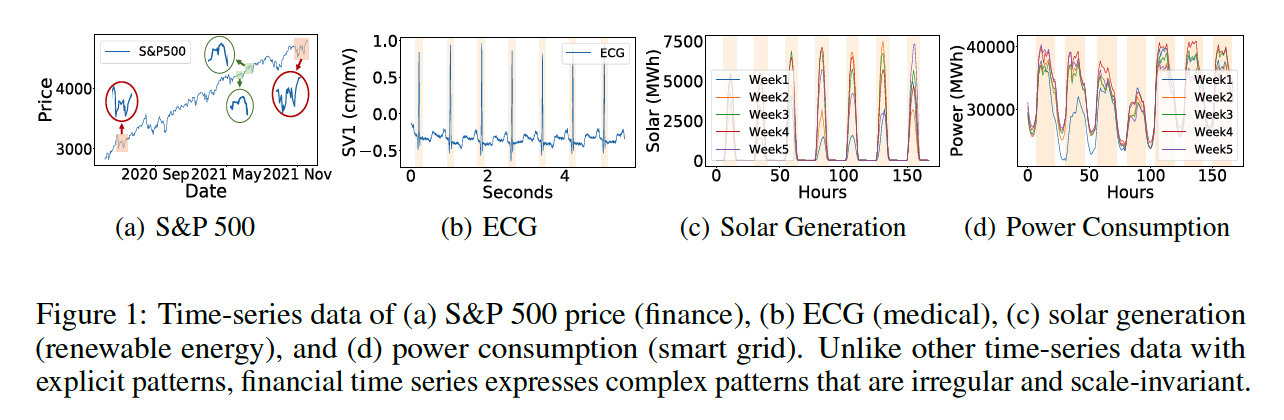
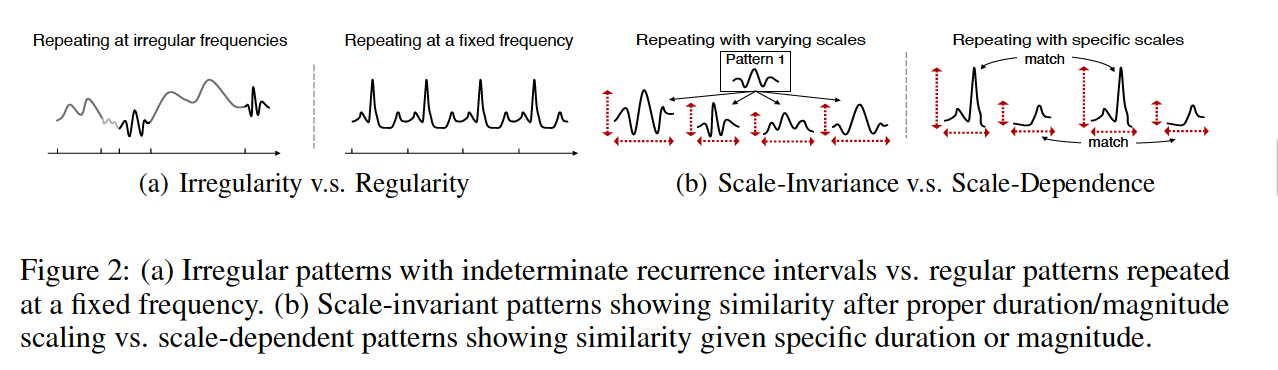
Solution

Deconstruct financial TS into 3 prong process

• (1) Pattern Recognition
  • to identify irregular & scale-invariant patterns
• (2) Generation
  • to synthesize segments of patterns
• (3) Evolution
  • to connect the generated segments

Contribution

1. Identify & Define 2 properties in TS finance

   • Irregularity
   • Scale-invariance

   Propose novel FTS-Diffusion framework

2. Three modules

   • (1) Pattern Recognition: based on SISC (Scale-Invariant Subsequence Clustering) algorithm
     • incorporate DTW to capture irregular patterns
   • (2) Generation: consists of a diffusion-baseed network
     • conditional on the patterns learned by SISC
   • (3) Evolution: made up of pattern transition network
     • produce temporal evolution of consecutive patterns

3. Experiments on real world finance TS

2. Related Work

DGM (Deep Generative Modeling) in TS

• TimeVAE (2021): VAE to model trend & seasonality in TS
• RCGAN (2017) & MV-GAN(2020) : GAN for medical TS
• TimeGAN (2019): GAN for general TS
• QuantGAN (2020): GAN for financial TS
• CSDI (2021): Score-based diffusion … unconditional version can be used as generative model
• DiffWave (2021) & BinauralGrad (2022): Generate waveform TS with diffusion models

\(\rightarrow\) Common Limitation: Model TS with REGULAR patterns

3. Problem Statement

(1) Unique characteristics of Financial TS

Propose a novel framework to model (1) irregular & (2) scale-invariant TS

Notation

• \(\boldsymbol{X}=\left\{\boldsymbol{x}_1, \ldots, \boldsymbol{x}_M\right\}\) : MTS of \(m\) segments

  • \(\boldsymbol{x}_m=\left\{x_{m, 1}, \ldots, x_{m, t_m}\right\}\).
  • Total Length: \(T=\sum_{m=1}^M t_m . \boldsymbol{x}_m\)

• Sampled from a conditional distribution \(f(\cdot \mid p, \alpha, \beta)\)

  • pattern \(p \in \mathcal{P}\),
  • duration is scaled by \(\alpha\) and magnitude scaled by \(\beta\).

  \(\rightarrow\) \(\boldsymbol{x}_m\) will be statistically similar to its underlying pattern \(p\) while allowing for adjustments in duration and magnitude.

To model the dynamics across patterns, we employ a Markov chain

• Tuple \((p, \alpha, \beta)\) : State
• \(Q\left(p_j, \alpha_j, \beta_j \mid p_i, \alpha_i, \beta_i\right)\) : State transition probabilities

(2) Problem Statement

Seek to operationalize the structure laid out in Sec. 3.1

No knowledge of …

• the segments \(\left\{\boldsymbol{x}_m\right\}_{m=1}^M\)
• the set of scale-invariant patterns \(\mathcal{P}\)
• the scaling factors \(\alpha\) and \(\beta\)
• the transition probabilities \(Q\left(p_j, \alpha_j, \beta_j \mid p_i, \alpha_i, \beta_i\right)\).

Goal : develop a data-driven framework to accomplish the following:

• (Pattern Recognition)
  • identify the patterns \(\mathcal{P}\)
  • group segments into clusters according to their patterns \(p \in \mathcal{P}\);
• (Pattern Generation)
  • learn the distribution \(f(\cdot \mid p, \alpha, \beta), \forall p \in \mathcal{P}\);
• (Pattern Evolution)
  • learn the pattern transition probabilities \(Q\left(p_j, \alpha_j, \beta_j \mid p_i, \alpha_i, \beta_i\right)\).

4. FTS-Diffusion Framework

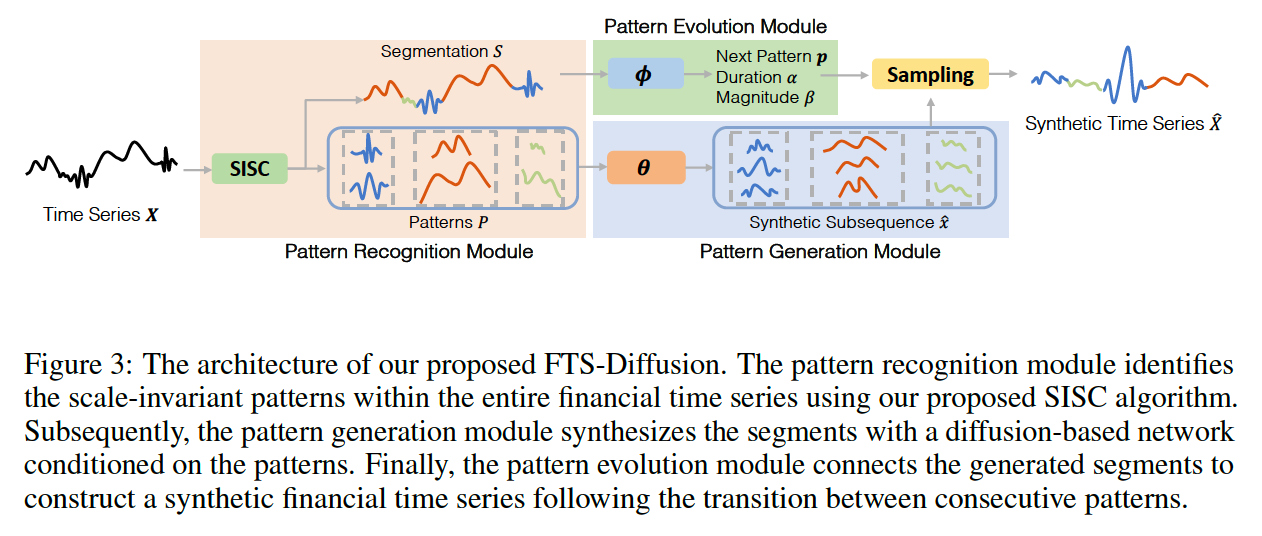
(1) Pattern Recognition

Goal: Identify Irregular & Scale-invariant patterns

Propose novel Scale-Invariant Subsequence Clusterint (SISC) algorithm

• To partition entire TS into segments of variable length … itno \(K\) clusters

  ( same cluster = similar shape (DTW-based) )

• Use K-means
• Greedy segmentation strategy

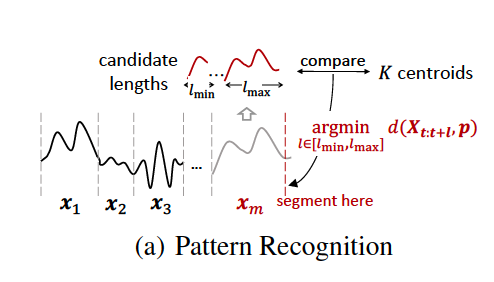
Distance metric: \(d(\cdot, \cdot)\)

• DTW: Robust to varying lengths & magnitudes
• \(D T W(\boldsymbol{x}, \boldsymbol{y}):=\min _{A \in \mathcal{A}}\langle A, \Delta(\boldsymbol{x}, \boldsymbol{y})\rangle\).
  • \(A\) : Alignment between two sequences in the set of all possible alignments
  • \(\Delta(x, y)=\left[\delta\left(x_i, y_j\right)\right]_{i j}\) : Pointwise distance matrix between two sequences \(\boldsymbol{x}\) and \(\boldsymbol{y}\).

(2) Pattern Generation

Goal: Learn pattern-conditioned temporal dynamices

Propose a pattern generation module \(\theta\)

[First network] Pattern-conditioned diffusion network

• Conditional denoising process
  • Forward: \(\boldsymbol{x}^N=\boldsymbol{x}^0+\sum_{i=0}^{N-1} \mathcal{N}\left(\boldsymbol{x}^{i+1} ; \sqrt{1-\beta}\left(\boldsymbol{x}^i-\boldsymbol{p}\right), \beta I\right)\)
  • Backward: \(\boldsymbol{x}^0=\boldsymbol{x}^N-\sum_{i=0}^{N-1} \epsilon_\theta\left(\boldsymbol{x}^{i+1}, i, \boldsymbol{p}\right)\)

[Second network] Scaling AE

• learn the transformation btw variable length \(x\) and fixed length \(x^{0}\)

\(\rightarrow\) Jointly train two networks

• \(\mathcal{L}(\theta)=\mathbb{E}_{\boldsymbol{x}_m}\left[ \mid \mid \boldsymbol{x}_m-\hat{\boldsymbol{x}}_m \mid \mid _2^2\right]+\mathbb{E}_{\boldsymbol{x}_m^0, i, \epsilon}\left[ \mid \mid \epsilon^i-\epsilon_\theta\left(\boldsymbol{x}_m^{i+1}, i, \boldsymbol{p}\right) \mid \mid _2^2\right]\).

(3) Pattern Evolution

Pattern evolution network

\(\left(\hat{p}_{m+1}, \hat{\alpha}_{m+1}, \hat{\beta}_{m+1}\right)=\phi\left(p_m, \alpha_m, \beta_m\right)\).

• where \(\left(\hat{p}_{m+1}, \hat{\alpha}_{m+1}, \hat{\beta}_{m+1}\right)\) denotes the next pattern & scales in length and magnitude.

Loss function

• \(\mathcal{L}(\phi)=\mathbb{E}_{\boldsymbol{x}_m}\left[\ell_{C E}\left(p_{m+1}, \hat{p}_{m+1}\right)+ \mid \mid \alpha_{m+1}-\hat{\alpha}_{m+1} \mid \mid _2^2+ \mid \mid \beta_{m+1}-\hat{\beta}_{m+1} \mid \mid _2^2\right]\).