(알고리즘과 자료구조) 알고리즘

(알고리즘과 자료구조) 알고리즘

Contents

1. 알고리즘 복잡도
2. 시간 복잡도
3. 정렬 (Sort)
   1. 버블 정렬 (Bubble Sort)
   2. 삽입 정렬 (Insertion Sort)
   3. 선택 정렬 (Selection Sort)
4. 공간 복잡도
5. 재귀 용법/호출 (Recursive Call)

6. 동적 계획법 (Dynamic Programming) & 분할 정복 (Divide and Conquer)

7. 고급 정렬
   1. 퀵 정렬 (Quick Sort)
   2. 병합 정렬 (Merge Sort)
8. 탐색 알고리즘
   1. 이진 탐색 (Binary Search)
   2. 순차 탐색 (Sequential Search)
9. 그래프
10. 그래프 기본 탐색 알고리즘
11. 탐욕 알고리즘
12. 그래프 고급 탐색 알고리즘
    1. 최단 경로 알고리즘
    2. 다익스트라 알고리즘

(1) 알고리즘 복잡도

1. 시간 복잡도 ( Time Complexity ) : 실행 속도

   \(\rightarrow\) 핵심 : for loop 의 횟수

2. 공간 복잡도 ( Space Complexity ) : 메모리 크기

(2) 시간 복잡도

• [최악의 경우] Big-O 표기법 : \(O(N)\)

• [최상의 경우] Omega 표기법 : \(\Omega(N)\)

• [평균의 경우] Theta 표기법 : \(\Theta(N)\)

Big-O 표기법 : \(O(N)\)

• 입력 \(N\) 에 따라, 몇 번의 실행이 이루어지는지!

• \(O(1) < O(\log n) < O(n) < O(n \log n) < O(n^2) < O(2^n) < O(n!)\).
• example)
  • \(N\)이 뭐든, 상수 회 시행 : \(O(1)\)
  • \(N\)에 따라, \(2N\), \(99999N\) 회 시행 : \(O(N)\)
  • \(N\)에 따라 \(32N^2+ 9999\) 회 시행 : \(O(N^2)\)

Example : 1 ~ n 까지의 합

• sum1 : \(O(N)\)
• sum2 : \(O(1)\)

def sum1(n):
  total = 0
  for i in range(1,n+1):
    total += i
  return total

def sum2(n):
  total = n*(n+1)/2
  return total

(3) 정렬 ( Sort )

a) 버블 정렬 ( Bubble Sort )

• 방법 : 2개의 인접한 데이터 비교 \(\rightarrow\) 작은거 LEFT, 큰거 RIGHT

• 코드 :

for bubble_sort(data):
  N = len(data)
  for idx in range(N):
    swap = 0
    for idx2 in range(N-1-idx):
      if data[idx2] > data[idx2+1]:
        data[idx2], data[idx2+1] = data[idx2+1], data[idx2]
        swap +=1
    if swap == 0:
      break
  return data

시간 복잡도 : \(O(N^2)\)

• 최악의 경우 : \(\frac{N*(N-1)}{2}\)
• 최고의 경우 : \(O(N)\)

b) 삽입 정렬 ( Insertion Sort )

• 방법 :

  • 2번째 index 부터 시작.

  • 해당 index 앞에 있는 데이터(1번째 index의 데이터) 부터 비교한다.

    현재 (2번째) 데이터보다 작은 값이 나올때까지 계속 앞으로 나아간다.

    나보다 작은 값이 나타나면, 그 값 바로 뒤에 놓는다

• 코드

def insertion_sort(data):
  N = len(data)
  for idx in range(N-1):
    for idx2 in range(idx+1,0,-1):
      if data[idx2] > data[idx2-1]:
        data[idx2], data[idx2-1] = data[idx2-1], data[idx2]
      else:
        break

시간 복잡도 : \(O(N^2)\)

• 최악의 경우 : \(\frac{N*(N-1)}{2}\)
• 최고의 경우 : \(O(N)\)

c) 선택 정렬 ( selection sort )

• 방법 :
  • 주어진 데이터 중, min값을 찾는다
  • 해당 min값을, 현재 데이터의 “맨 앞 값”과 교체한다
  • 맨 앞의 값을 제외하고, 위 과정을 반복
• 코드

def selection_sort(data):
  N = len(data)
  for stand in range(N-1):
    min_idx = stand
    for idx in range(stand+1, N):
      if data[idx] < data[min_idx]:
        min_idx = index
    data[min_idx], data[idx] = data[idx], data[min_idx]
  return data

시간 복잡도 : \(O(N^2)\)

• 최악의 경우 : \(\frac{N*(N-1)}{2}\)
• 최고의 경우 : \(O(N)\)

(4) 공간 복잡도

\(S(P) = c + S_p(n)\).

• \(c\) : 고정 공간 ( 알고리즘과 관련 X )
• \(S_p(n)\) : 가변 공간 ( 알고리즘과 관련 O )

Example ) **n! 구하기 **( 방법 1 )

• 변수 n, fac, index만 필요함 ( 3개의 값 )
• 따라서, 공간 복잡도는 \(O(1)\)

def factorial(n):
  fac = 1
  for idx in range(2,n+1):
    fac = fac*idx
  return fac

Example ) **n! 구하기 **( 방법 2 )

• 재귀 함수 사용
• n에 따라, 변수 n이 총 n번 만들어짐
• 따라서, 공간 복잡도는 \(O(n)\)

def factorial(n):
  if n>1:
    return n*factorial(n-1)
  else:
    return 1

(5) 재귀 용법/호출 ( Recursive Call )

( 고급 sorting 알고리즘에서 사용 )

• 함수 안에서 동일한 함수를 호출

Example ) **n! 구하기 **( 위의 방법 2 )

def factorial(n):
  if n>1:
    return n*factorial(n-1)
  else:
    return 1

• 시간 복잡도 : \(O(n)\)
• 공간 복잡도 : \(O(n)\)

재귀 호출은 스택(stack)의 전형적인 예시이다

(6) 동적 계획법 ( Dynamic Programming ) & 분할 정복 ( Divide and Conquer )

동적 계획법 ( Dynamic Programming (DP) )

• 상향식 접근 : 작은 부분 문제 해결 후, 이를 활용하여 큰(전체) 문제를 해결

  • 그러기 위해, Memoization 기법을 사용

    ( 작은 부분 문제의 결과를 기억해야 )

  • 큰 문제를 작은 문제로 쪼갤 때, 부분 문제는 중복 & 재활용됨

• Ex) 피보나치 수열

분할 정복 ( Divide and Conquer )

• 하향식 접근 :
  • 하나의 전체/큰 문제를, 나눌 수 없을 때까지 잘게 나눈다
  • 나눠진 작은 문제들을 해결하고, 이를 합병하여 문제의 답을 얻음
  • 상위의 답을 얻기 위해, 아래로 내려가면서 하위의 답을 구함
• Ex) 병합 정렬, 퀵 정렬

공통/차이점

공통점

• 큰 문제를 작은 문제로 나눔

차이점

• 동적 계획법
  • 부분 문제는 “중복”됨. 이 결과는 “재활용”됨
  • 따라서, Memoization 기법 사용
• 분할 정복
  • 부분 문제는 “중복되지 않음”
  • 따라서, Memoization 기법 사용 X

피보나치 수열

\(F_{n}:= \begin{cases}0 & \text { if } n=0 \\ 1 & \text { if } n=1 \\ F_{n-1}+F_{n-2} & \text { if } n>1\end{cases}\).

# RECURSIVE CALL 

def fibo_RC(n):
  if n<=1:
    return n
  return fibo(n-1) + fibo(n-2)

# DYNAMIC PROGRAMMING 

def fibo_DP(n):
  cache = [0 for _ in range(n+1)]
  cache[0] = 0
  cache[1] = 1
  
  for idx in range(2,n+1):
    cache[idx] = cache[idx-1] + cache[idx-2]
  return cache[n]

(7) 고급 정렬

a) 퀵 정렬 ( quick sort )

• 정렬 알고리즘의 꽃
• 기준점(pivot)을 정한 뒤,
  • 기준점보다 “작은” 데이터는 LEFT 에
  • 기준점보다 “큰” 데이트는 RIGHT 에

• Divide & Conquer (분할 & 정복) 알고리즘의 예

• 시간 복잡도 : \(O(n \log n\))

  • 맨 위의 단계 0 , \(n/2^2\) 는 단계 2

    ( 각 단계에는 \(2^i\) 개의 노드가 존재 )

  • (a) 따라서, 각 단계는 \(2^i \times n/2^i\) = \(n\)

  • (b) 그러므로, 단계는 \(\log_2 n\) 개 만큼 만들어짐.

  • (a) x (b) \(\rightarrow\) \(O(n \log n)\)

def quick_sort(data):
  N = len(data)
  if N <=1:
    return data
  
  left, right = list(), list()
  pivot = data[0]
  
  for idx in range(1,N):
    left = [x for x in data[1:] if pivot > x]
    right = [x for x in data[1:] if pivot <= x]
     
  # Recursive Call
  return quick_sort(left) + [pivot] + quick_sort(right)

시간 복잡도 : \(O(n \log n)\)

• 최악의 경우 : \(O(n^2)\) ………… pivot이 가장 크거나/가장 작을 경우

b) 병합 정렬 ( merge sort )

• 재귀 호출 (Recursive Call)을 활용한 대표적인 알고리즘

• 분할 & 정복 (Divide & Conquer)을 활용한 대표적인 알고리즘

  ( 동적 계획법 처럼 Memoization을 수행하진 않음 )

• 크게 2개의 단계로 구성

  • (1) split 단계 ( 더 이상 분리할수 없을 때 까지! )
  • (2) merge 단계

• 방법

  • step 1) 리스트를 1/2로 나눔 ( 좌 & 우 )
  • step 2) 각 부분을 재귀적으로 합병 정렬
  • step 3) 그런 뒤, 다시 둘을 합침

(1) split 함수

def split(data):
  N = len(data)
  med = int(N/2)
  L = data[:med]
  R = data[med:]
  return (L,R)

(2) merge 함수

def merge(L,R):
  merged = list()
  L_idx, R_idx = 0, 0
  N_L = len(L)
  N_R = len(R)
  
  # case 1) L & R 잔여
  while (N_L > L_idx) & (N_R > R_idx):
    if L[L_idx] > R[R_idx]:
      merged.append(R[R_idx])
      R_idx +=1
    else:
      merged.append(L[L_idx])
      L_idx +=1
      
  # case 2) L만 잔여
  while N_L > L_idx:
    	merged.append(L[L_idx])
      L_idx +=1
  # case 3) R만 잔여
  while N_R > R_idx:
    	merged.append(R[R_idx])
      R_idx +=1
      
  return merged

(3) merge sort = (1) + (2)

def merge_sort(data):
  N = len(data)
  if N<=1:
    return data
  med = int(N/2)
  L = merge_sort(data[:med])
  R = merge_sort(data[med:])
  return merge(L,R)

(8) 탐색 알고리즘

a) 이진 탐색 ( Binary Search )

example) 세팅

• 30개의 병뚜껑이 있다

  ( 각 병뚜껑은 1~100사이의 숫자 중 하나가 적혀있음 )

• 이 중, 70이 있는지를 확인해보자.

• 조건

  • (1) 병을 최소한으로 따야함
  • (2) 각 병뚜껑은 “오름차순” 순으로 나열되어 있음

분할 정복 & 이진 탐색

• 분할 정복 ( Divide and Conquer )
  • Divide : 문제를 잘게 나누자
  • Conquer : 작은 문제를 풀자 ( 풀기 불가능하면, 더 나누자 )
• 이진 탐색 ( Binary Search )
  • Divide : list를 2개의 sub-list로 나누기
  • Conquer :
    • (1) search > 중간값 : RIGHT sub-list에서 찾기
    • (2) search < 중간값 : LEFT sub-list에서 찾기

알고리즘 복잡도

• \(n\) 개의 요소를 가진 list

• 매번 2로 나누어, 1이 될때까지 총 \(k\) 번의 비교를 진행

• \(n \times 1/2 \times 1/2 \cdots =1\).

• \(n \times 1/2^k\) = \(1\)

  \(\rightarrow\) \(k= \log_2n\)

• \(k+1\) 이 최종 시간 복잡도!

• 때문에, \(O(k+1) =O(\log_2n+1) = O(\log_2n)\)

def binary_search(data, x):
  
  N = len(data)
  if N==1 & x==data[0]:
    return True
  if N==1 & x!= data[0]:
    return False
  if N==0:
    return False
 
	med = N//2
  if x == data[med]:
    return True
  else:
    if x > data[med:]:
      return binary_search(data[med:], x)
  	else:
      return binary_search(data[:med], x)

b) 순차 탐색 ( Sequential Search )

• 앞에서부터 일일히 비교하여, 원하는 데이터를 찾음
• 시간 복잡도 : \(O(N)\)

def sequential_search(data, x):
  N = len(data)
  for idx in range(N):
    if data[idx] == x:
      return idx
  return -1

(9) 그래프

그래프 : (1) 노드 + (2) 엣지

각종 용어

• degree ( in-degree & out-degree )
• path length
• simple path : 처음 정점 & 끝 정점 제외, 중복된 정점이 없는 경우
• cycle : 단순 경로 (simple path)의 시작 & 종료 정점이 동일한 경우

그래프의 종류

• Undirected graph & Directed graph

• UnWeighted Graph & Weighted Graph
• Connected Graph & Disconnected Graph

사이클 & 비순환 그래프

• Cycle : 단순 경로의 시작=종료
• Acyclic Graph : cycle이 없는 그래프

완전 그래프 (Complete Graph)

• 모든 노드가 서로 연결되어 있는 경우

그래프 vs 트리

	그래프	트리
정의	노드 & 노드를 연결하는 엣지로 표현된 자료구조	그래프의 한 종류 (방향성 O는 비순환 그래프)
방향성	O & X	O
사이클	O & X	X
루트 노드	X	O
부모/자식 관계	X	O

(10) 그래프 기본 탐색 알고리즘

1) BFS (너비 우선 탐색)

2) DFS (깊이 우선 탐색)

(11) 탐욕 알고리즘 ( Greedy Algorithm )

• 최적의 해 를 구할때 사용
• 현재의 순간만을 고려(미래 고려 X) 해서, 최적이라 선택하는 것을 선택
• global optimal 보장은 당연히 X

Eample 1) 동전 문제

• 4720원 지불해야함. 가장 적은 개수의 동전 지불 방법?
• 동전 : 1/50/100/500원 동전

def coin_count(coins,money):
  cnt = 0
  result = list()
  coins.sort(reverse = True)
  for c in coins:
    c_num = money // c
    cnt += c_num
    money -= c_num * c
    result.append([c,c_num])
  return cnt, result

coins = [500,100,50,1]

coin_count(coins, 4720)

Example 2) 부분 배낭 문제

• kg 한도가 주어짐. 이 안에 가치 극대화 물품 고르기

# (1) 가성비 (= value / kg) 좋은 순으로 정렬
kg_value = [(10,10), (15,12), (20,10), (25,8), (30,5)]
kg_value = sorted(kg_value, key = lambda x:x[1]/x[0], reverse=True)

def best_product(kg_value, capacity):
  kg_value = sorted(kg_value, key = lambda x:x[1]/x[0], reverse=True)
  total_val = 0
  result = []
  
  for kv in kg_value:
    if capacity - kv[0] >= 0:
      capacity -= kv[0]
      total_val += kv[1]
      num = 1
      result.append([kv[0],kv[1],num])
    else:
      num = capacity / kv[0]
      total_val += kv[1]*num
      result.append(kv[0],kv[1], num)
    	break
      
	return total_val, result

kg_value = [(10,10), (15,12), (20,10), (25,8), (30,5)]
capacity = 30

best_product(kg_value, capacity)

(12) 그래프 고급 탐색 알고리즘

a) 최단 경로 알고리즘

2 node를 연결하는 최단 경로 찾기

( 일반적으로 weighted graph를 가정함 )

문제의 종류

• (1) 단일 출발 + 단일 도착
  • ex) A ~ B까지
• (2) 단일 출발
  • ex) A ~ 모든 노드들까지
• (3) 전체 쌍
  • ex) (A,B),(A,C) … (Y,Z) 사이

b) 다익스트라 알고리즘

( 위의 문제 (2) 단일 출발 을 푸는 알고리즘 )

• BFS와 유사
• 우선순위 큐 (Priority Queue)를 활용

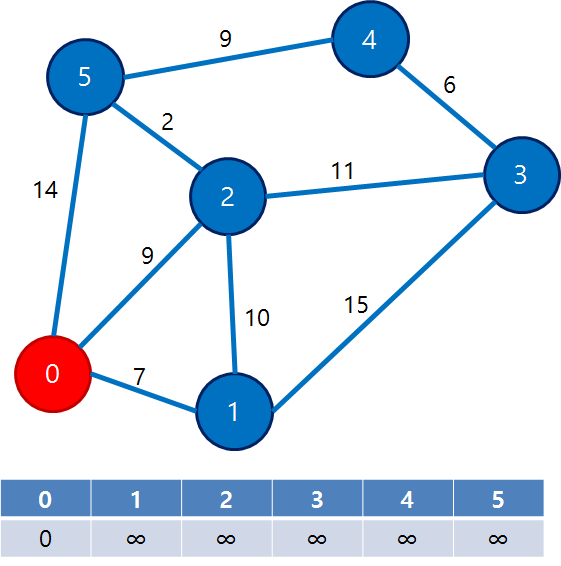
Step 1)

• 첫 정점을 기준으로 배열(거리를 기록해두는 배열)을 선언
• 해당 배열에, (첫 정점 & 각 정점) 사이의 거리 저장 ( 본인은 0, 나머지는inf 로 저장 )
• 우선순위 큐에, (첫 정점, 거리0) 1개를 우선 넣음

Step 2)

• 우선순위큐에서 노드 1개 꺼냄 ( 1개밖에 없으니, 첫 정점을 꺼낼 것 )
• 해당 노드에 인접한 노드에 대해,
  • [배열 업데이트] 첫 정점 ~ 각 노드에 대한 거리 비교 & 업데이트
  • [우선순위 큐에 삽입] 위의 업데이트 값을 우선순위로 삼고, 우선순위큐에 넣기

위의 Step2) 과정을 반복하고, 우선순위큐에 꺼낼 노드가 없으면 끝