(CS224W) 4.Link Analysis, Page Rank

[ 4. Link Analysis, Page Rank ]

( 참고 : CS224W: Machine Learning with Graphs )

Contents

• 4-1. Introduction
• 4-2. Page Rank
• 4-3. Personalized Page Rank (PPR)
• 4-4. Matrix Factorization

4-1. Introduction

by treating graph as a MATRIX, we can..

• 1) Random Walk : determine node’s importance
• 2) Matrix Factorization : node embedding
• 3) Other node embeddings

Web as a graph

• many links are “transactional” ( linked to each other )

• not all pages are equally important

  \(\rightarrow\) RANK the pages!

  ( the more link, the more important the pages are! )

Link Analysis algorithms

• 1) Page Rank
• 2) Personalized Page Rank (PPR)
• 3) Random Walk with Restarts

4-2. Page Rank

(1) Link’s Vote

• proportional to the importance of its source page

• page is more important, if it is pointed to by other important pages

  ex)

  • (link 1) A is friend of B, who have 10,000 friends
  • (link 2) A is friend of C, who have 10 friends

  \(\rightarrow\) (link 2)’s vote > (link 1)’s vote

• A’s importance is sum of all the votes of A’s link

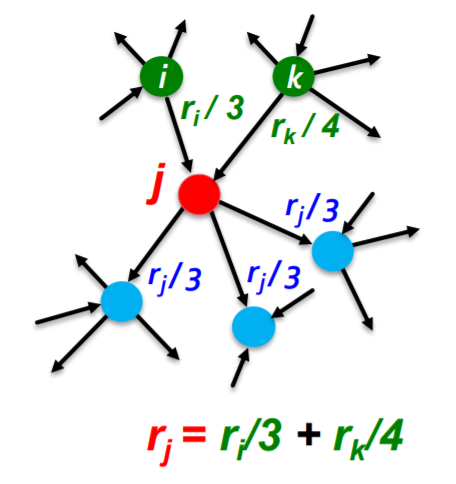
(2) Rank

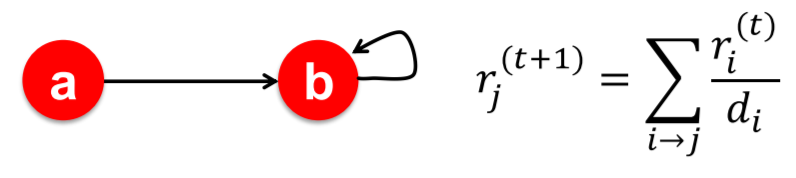
Rank of node \(j\) ( = \(r_j\) )

• \(r_{j}=\sum_{i \rightarrow j} \frac{r_{i}}{d_{i}}\),

  where \(d_{i} \ldots\) out-degree of node \(i\)

Example )

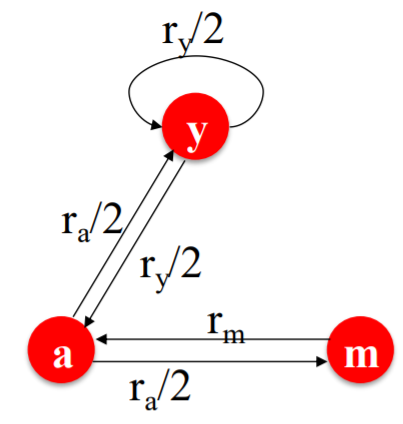
To solve the problem above….

[ Flow Equation ]

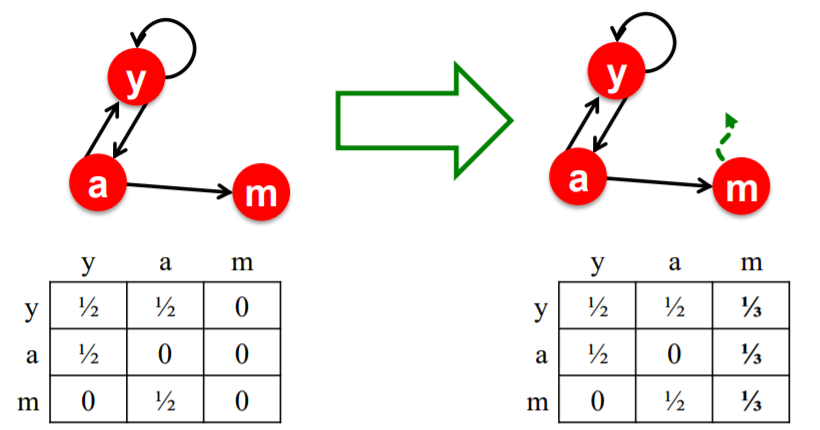
\(\begin{aligned} &r_{y}=r_{y} / 2+r_{a} / 2 \\ &r_{a}=r_{y} / 2+r_{m} \\ &r_{m}=r_{a} / 2 \end{aligned}\).

(3) Matrix Formulation

express “Flow Equation” with matrix : \(r = M \cdot r\)

• (1) \(r\) : Rank vector
  • \(r_i\) : importance score of page \(i\)
  • \(\sum_i r_i =1\).
• (2) \(M\) : Stochastic adjacency matrix
  • \(d_i\) : out-degree of node \(i\)
  • if \(i \rightarrow j\) , then \(M_{ij} = \frac{1}{d_i}\) ( colsum = 1)

(4) Random Walk

Random Walk \(\approx\) surfer moves from pages to pages ( where there is a link )

Finding a stationary distribution

• \(p(t)\) : vector, whose \(i\)th coordinate is the probability that the surfer is at page \(i\) at time \(t\)
• \[p(t+1) = M \cdot p(t) = p(t)\]
• \(r\) ( Rank vector) should satisfy \(r = M \cdot r\)

(5) Page Rank

Eigenvector of Matrix

• \(\lambda c = A c\).
  • \(c\) : eigenvector
  • \(\lambda\) : eigenvalue
• Flow Equation : \(1 \cdot r= M \cdot r\)
  • \(r\) ( rank vector ) : eigenvector of \(M\), with eigenvalue 1
• Long-term distribution : \(M(M(..M(Mu)))\)

\(r\) : (1) = (2) = (3)

• (1) Page Rank
• (2) principal eigenvector of \(M\)
• (3) stationary distribution of a random walk

(6) Solving Page Rank

“iterative procedure”

• step 1) assign initial page rank ( to all nodes )
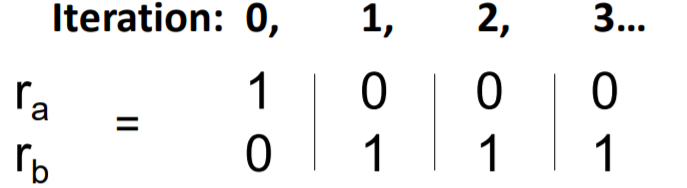
• step 2) repeat until convergence \(\left(\sum_{i} \mid r_{i}^{t+1}-r_{i}^{t} \mid <\epsilon\right)\).
  • updating equation : \(r_{j}^{(t+1)}=\sum_{i \rightarrow j} \frac{r_{i}^{(t)}}{d_{i}}\).
    • \(d_{i} :\) out-degree of node \(i\)

Power Iteration

Settings

• \(N\) nodes : pages
• Edges : hyperlinks

Power iteration

( simple iterative procedure )

• step 1) initialize \(\boldsymbol{r}^{(0)}=[1 / N, \ldots, 1 / N]^{T}\).

• step 2) Until \(\mid \boldsymbol{r}^{(\boldsymbol{t}+\mathbf{1})}-\boldsymbol{r}^{(t)} \mid _{1}<\varepsilon\)….

  • iterate \(\boldsymbol{r}^{(\boldsymbol{t}+\mathbf{1})}=\boldsymbol{M} \cdot \boldsymbol{r}^{(t)}\). ( in matrix formulation )

    ( \(r_{j}^{(t+1)}=\sum_{i \rightarrow j} \frac{r_{i}^{(t)}}{d_{i}}\) ( in vector formulation ) )

• ( about 50 iterations )

Example

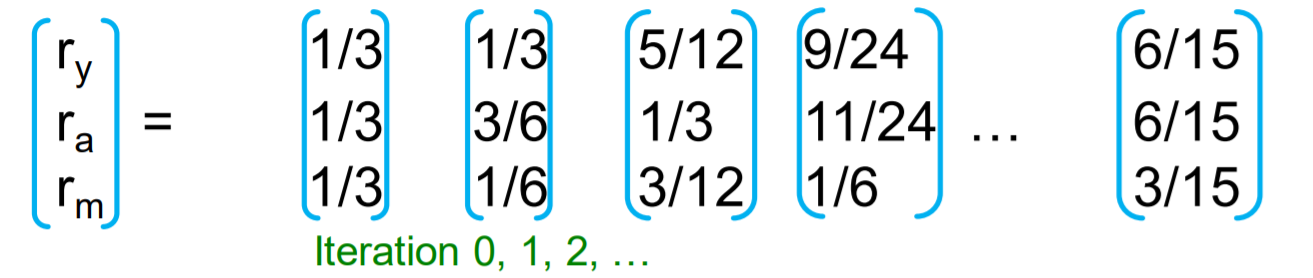
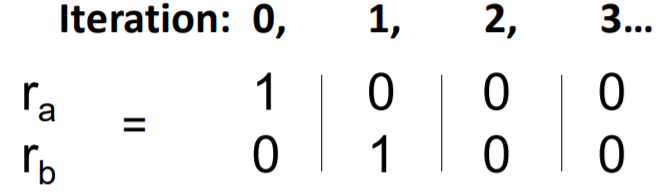
(7) Problems of Page Rank

1. Dead ends

• no out-links ( nowhere to go! )
• importance leakage

1. Spider traps

• all out-links are within the group ( only looping in the same area! )
• absorbs all the importance

Solution 1 # Spider traps

• Two options, when surfing
  • option 1) jump to LINK
    • with prob \(\beta\)
  • option 2) jump to RANDOM
    • with prob \(1-\beta\)
• then, will be able to teleport out of the trap

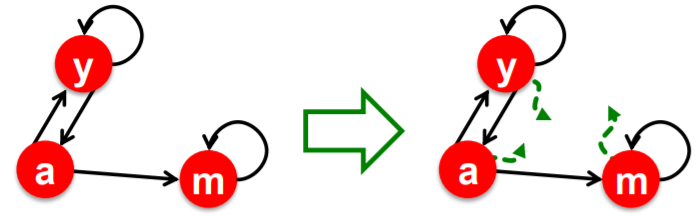
Solution 2 # Dead ends

• follow random teleport links with total probability 1.0 from dead-ends

Is it really a problem?

(1) Spider Traps

• NOT a problem

  ( but PageRank is not the score that we want )

(2) Dead-ends

• IS a problem
  • does not meet our assumption ( STOCHASTIC matrix )

(8) Random Teleports

Two options, when surfing

• 1) jump to LINK …… with prob \(\beta\)
• 2) jump to RANDOM ………with prob \(1-\beta\)

Page Rank Equation

\(r_{j}=\sum_{i \rightarrow j} \beta \frac{r_{i}}{d_{i}}+(1-\beta) \frac{1}{N}\).

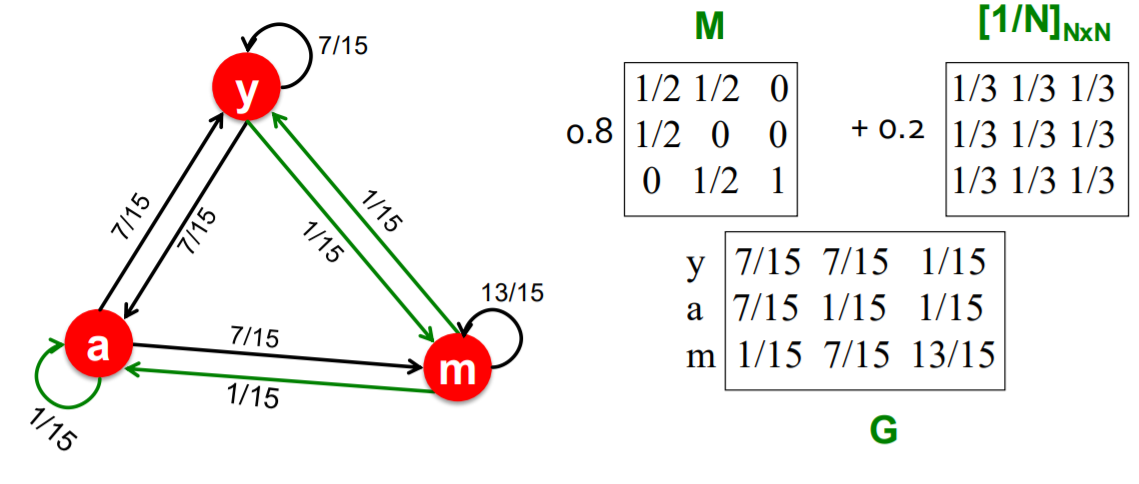
Google Matrix

\(G=\beta M+(1-\beta)\left[\frac{1}{N}\right]_{N \times N}\).

• with \(\beta =0.8,0.9\) : make 5 steps on average
• use this \(G\) as stochastic adjacency matrix ! ( \(r = Gr\) )

Example : \(\beta = 0.8\)

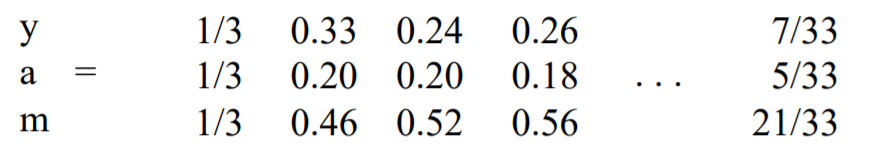
4-3. Personalized Page Rank (PPR)

Need for “PERSONALIZED” page rank

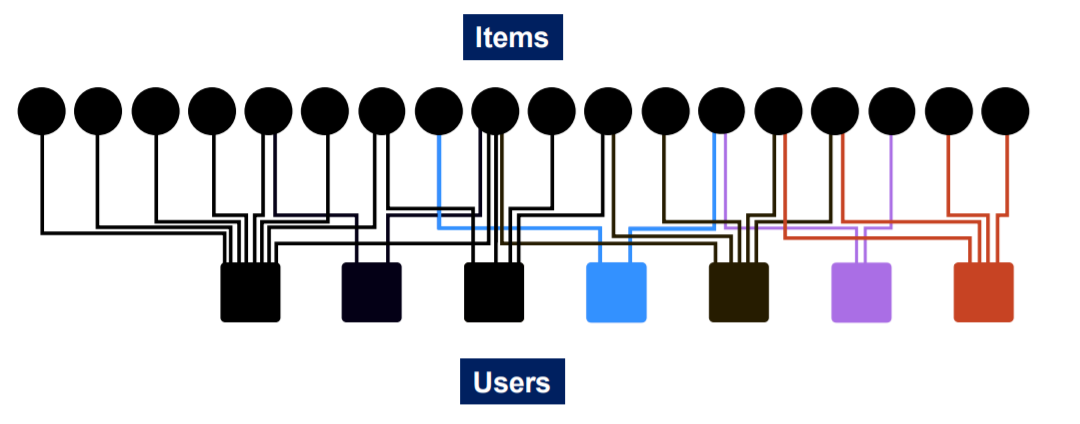
ex) Recommender System

• form of graph : “bipartite graph”
• all the users have their OWN characteristics

(1) Extension of Page Rank

1) Page Rank

• teleports to “ANYWHERE” in the graph
  

2) Personalized Page Rank

• teleports to “SUBSET (\(S\))” of the graph
  

3) Proximity on Graphs

• teleports to “SUBSET (\(S\))” of the graph,

  where subset is a “SINGLE NODE” (\(S = \{Q\}\))

• called “Random Walks with Restarts”

(2) Random Walk

• Basic idea : every node is EQUALLY IMPORTANT

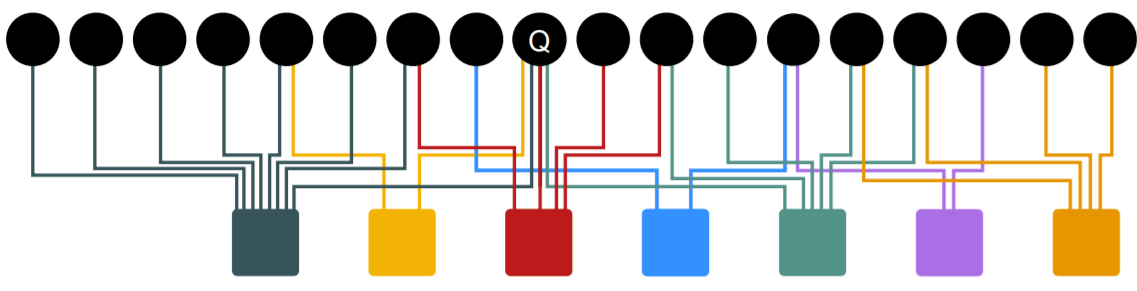
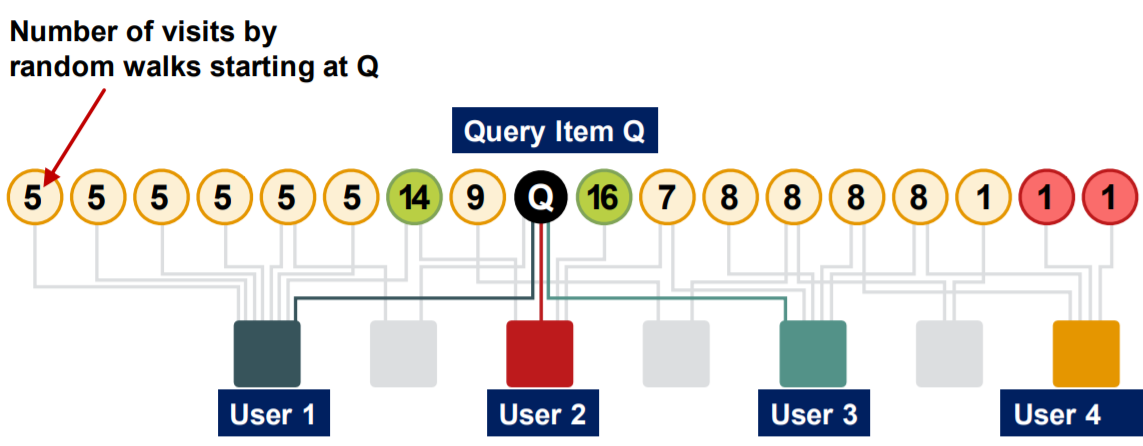
• Simulation : given a query node..

  • step 1) make a random step ( to neighbor )
    • record a visit ( count = count+1 )
  • step 2)
    • (with prob \(\alpha\)) RESTART
    • (with prob \(1-\alpha\)) KEEP GOING

• nodes with “highest count”

  = “highest proximity” to query node

(3) Advantages

Proximity (Similarity) defined as above considers…

• 1) multiple connections
• 2) multiple paths
• 3) direct/indirect connections
• 4) degree of the node

(4) Summary

Page Rank

• limiting distribution of the surfer location represented node importance
• leading eigenvector of transformed adjacency matrix \(M\)

1) Page Rank

• teleports to “ANYWHERE” in the graph
• \(\boldsymbol{S}=[0.1,0.1,0.1,0.1,0.1,0.1,0.1,0.1,0.1,0.1]\).

2) Personalized Page Rank

• teleports to “SUBSET (\(S\))” of the graph
• \(\boldsymbol{S}=[0.1,0,0,0.2,0,0,0.5,0,0,0.2]\).

3) Proximity on Graphs

• teleports to “SUBSET (\(S\))” of the graph,

  where subset is a “SINGLE NODE” (\(S = \{Q\}\))

• \(\boldsymbol{S}=[0,0,0,0,1,0,0,0,0,0,0]\).

4-4. Matrix Factorization & Node embeddings

(1) Introduction

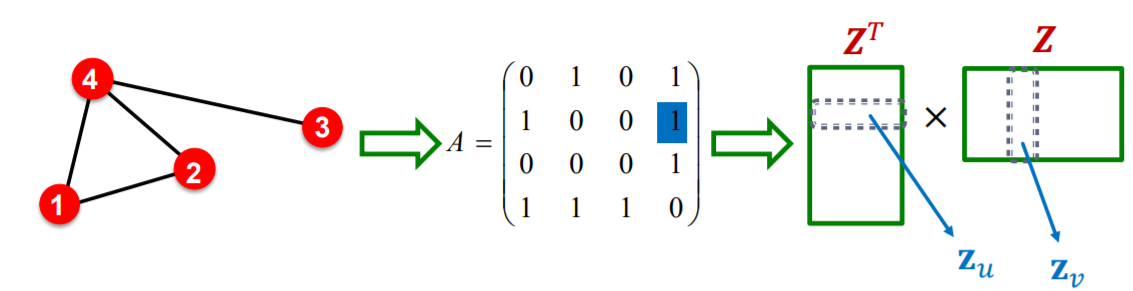
Notation

• \(Z\) : embedding matrix ( of all nodes )

• \(z_v\) : embedding vector ( of node \(v\) )

  ( both are \(d\) (\(<<n\) ) dimension )

Goal

• MAXIMIZE \(z_v^T z_u\) for all node pairs \((u,v)\) that are SIMILAR

• so, how do we define similarity ?

  • ex) similar, if CONNECTED by edge!

    ( that is, \(z_v^T z_u = A_{u,v}\) & \(Z^TZ=A\) )

(2) Matrix Factorization

learn \(Z\), such that…

• \(\min _{\mathbf{Z}} \mid \mid A-\boldsymbol{Z}^{T} \boldsymbol{Z} \mid \mid _{2}\).

so, how to factorize \(A\)

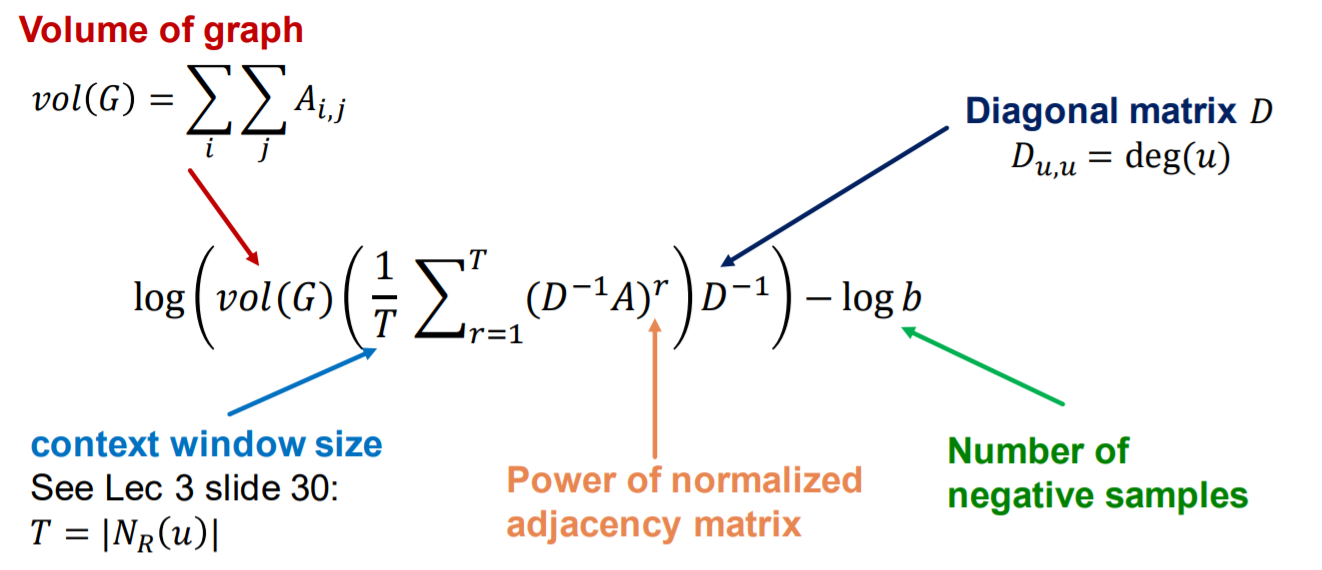
(3) Random-walk based similarity

Deep Walk, Node2vec

Both algorithms…

• have their own “similarity”, based on “random walk”
• can be seen as “matrix factorization”

Deep Walk’s matrix factorization

(4) Limitations

• 1) can not obtain embedding of the node that are NOT in the TRAINING SET

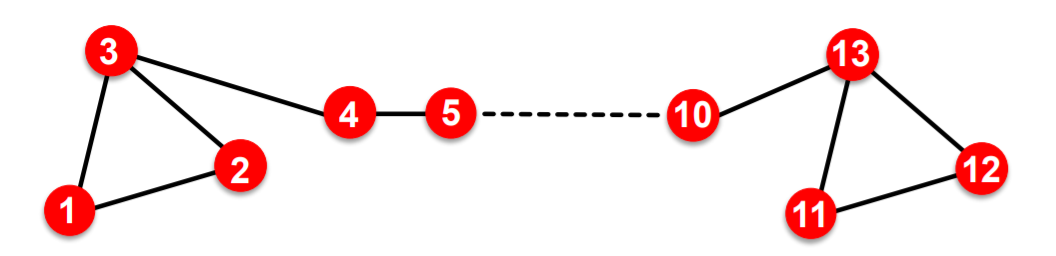
• 2) can not capture STRUCTURAL SIMILARITY

  • ex) node 1 & node 11 may have similar role, but may have very different embeddings!

    

• 3) can not utilize NODE/EDGE/GRAPH features

\(\rightarrow\) solution : Deep Representation Learning & GNN